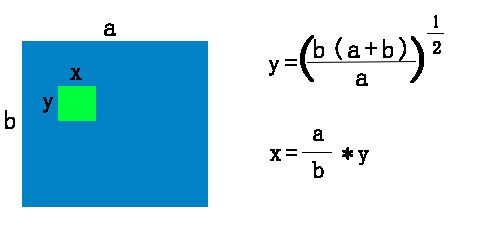图像的自适应二值化

机器视觉分为三个阶段 : 图像转化、图像分析、图像理解。若要将一幅图像转化为方便分析理解的格式，有一个很关键的过程就是“图像二值化”。一幅图像能否分析理解的准确很大程度上来说取决于二值化效果的好坏。然而目前国际上还没有任何二值化标准的算法，也没相关的确定性数学模型建立。这里我大致介绍我这几天研究的鄙见。

在二值化前有一个很重要的步骤是“图像灰度化”，原理就是将原RGB图像的三维矩阵进行f(x) = R*0.3+G*0.51+B*0.11运算得到一个二维矩阵（个人认为一个维度承载着一类信息，一维图像能够传达一根线的信息，二维图像能传达一幅图片信息，而这第三维便是颜色信息，所以三维降到二维图像自然失去了颜色），至于函数的由来不得而知，还望有专业人士指教。

==灰度化==》》

二值化算法是取一个阈值，将大于阈值的像素点取值1即显示白色，而小于阈值的像素点自然赋值为0即显示为黑色。所以这个阈值确定的好坏直接影响到效果。最简单的阈值取定便是取整幅图画的均值mean了:

==均值二值化==》

上述效果感觉还不错，但是对于某些图效果就没这么乐观了，比如

==均值二值化==》

这类受到光线阴影而影响到降低均值的图片，部分阴影区域的像素点会比均值低，所以可能会在阴影区域出现死黑的区域，所以单一的取均值来二值化是不够完美的。

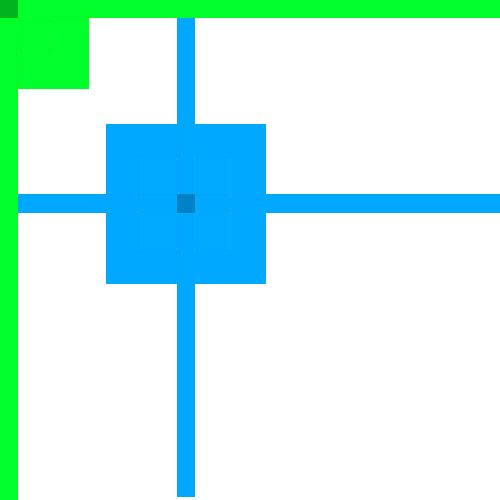
让我们来思考下原因：这个整幅图像的均值可以认为是整幅图像信息的一个综合数据，将像素点与均值比对在一定程度上可以理解为该像素点与整幅图像的关系。但是一个像素点真的会与整幅图像的所有像素点都有关系么？答案当然是否定的，我查阅了一些资料，有一种叫做自适应二值化的算法（每个像素点比对的阈值不同的算法总称），他将二维矩阵合成一行，然后将每个像素点与前面一定范围内像素点通过某种方法计算出来的值进行比对，这种算法出来的图像可以说是携带了行方向的像素点关系，但是在列方向上的呢？所以我加了些改进，糅合了行列方向信息的算法，我给他取名为“十字二值化算法”，即每一个像素点的阈值取它所在的行列的所有像素点的均值mean1：

做出的效果如下

虽然效果比取全局均值的效果要好一点点，在阴影区域已经显露出部分字体，但是效果并不令人满意。

仔细想想，像素点的信息是否与所处的行列都有关呢？很大的可能性是只与较近的十字像素区域有关，较远的则很少有关了。进一步思考，阴影部分像素点在全局面前也许是个黑点，但在其周围附近却可能是个白点，是否与较近的一块矩形区域内的像素点有关呢？我们不妨尝试下，像素点个数为行列像素个数之和，矩形区域的长宽比与图像的长宽比相同，容易推出公式（我把它名为“矩阵二值化算法”）：

括号里的（a+b）为自己设定的小矩阵的像素点个数，可以自行设定。我们把这么一个小矩阵称为颗粒，把矩阵的大小称之为颗粒度，理所当然一幅图像，颗粒度越大则颗粒越少，反之越多。而均值二值化即可认为整幅图像为一个颗粒度。后面我们将会意识到颗粒度的大小会对图像有很大的影响。这里默认为a+b，有如下效果：

顿时眼前一亮！这是个突破！字体（细节）全部显现出来了，可为什么其他地方（平滑的区域）却出现了“麻点呢”？原因是这些区域内所求像素点附近矩阵内的所有像素点灰度值都极度相近，这造成所求像素点与附近像素点灰度值的均值也极度相近，那么会产生大约50比50的概率大于均值，所以在平滑的区域黑白几率也就一半一半了。这就上升到了一个局部与全局的权衡问题，要想故及全局，则会想均值二值化那样出现死黑区域，而想局部计算则会出现这样的乱点问题。那我们时候可以综合“十字二值化算法”和“矩阵二值化算法”来达到全局与局部的最平衡呢？这也就是我当初设置矩阵颗粒度为图像长+宽的原因了，将两者算法综合，算法各自涉及的像素点皆为长+宽个数，也是一半一半。平衡嘛！

我将他命名为“十字矩阵二值化算法”，其效果为：

能够开心的发现，图像效果像算法那样也综合了，虽然任然有瑕疵，但至少取得了一定的成功。

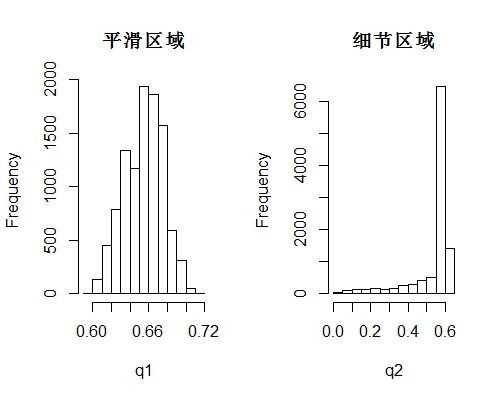
经过我一整夜的思考，我想无论我和权衡 十字二值化算法（处理平滑区域较好） 和 矩阵二值化算法（处理细节完美），始终会在全局和局部上有问题，所以我干脆摈弃这个权衡的思想，进而思考如何将 矩阵二值化算法 平滑区域的乱点去除。也就是如何分辨细节区域和平滑区域。因此我截取了部分细节区域和平滑区域，观察其值的直方图

可以观察到在平滑区域，像素点的灰度值在一个很小的区间，且呈现中间突出的分布曲线；而在细节区域，像素点的灰度值却分布在很大的一个区间，呈现出极端分布的规律，只要我们能正确区别两种区域便能有效处理图像。因此我在 “矩阵二值化算法” 中，像素点与矩阵内所有像素点的均值比对过程中加了一个参数β，即if( a ＜mean*β）,这个参数β经过我多张照片测试后调为0.9。其效果为：

效果终于达到了，细节得以体现，平滑区域也无半点影响。perfect！

———————————————————————————————————————————-

以下是R代码

binarization<-function(matrix,tar = '',rate = 0.9){
  if(length(dim(matrix)) == 3){
    matrix<-rgb_to_gray(matrix)
  }
  mat<-array(dim = dim(matrix))

  hh<-dim(matrix)[1]
  ww<-dim(matrix)[2]

  height<-sqrt(hh/ww*(hh+ww))
  width<-ww/hh*height

  for(i in 1:dim(matrix)[1]){
    for(k in 1:dim(matrix)[2]){
      h1<-i-floor(height/2)
      h2<-i+floor(height/2)
      w1<-k-floor(width/2)
      w2<-k+floor(width/2)
      if(h1<1)
        h1<-1
      if(w1<1)
        w1<-1
      if(h2>dim(matrix)[1])
        h2<-dim(matrix)[1]
      if(w2>dim(matrix)[2])
        w2<-dim(matrix)[2]
      mat[i,k]<-mean(matrix[h1:h2,w1:w2])
    }
  }

  mat[matrix*rate]<-0
  mat[mat!=0]<-1

  if(tar == ''){
    return(mat)
  }else{
    writeJPEG(image = mat,target = tar)
  }
}

———————————————————————————————————————————–

以下是多张图片的算法效果展示：

=======》》

=======》》

=======》》

=======》》