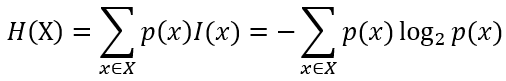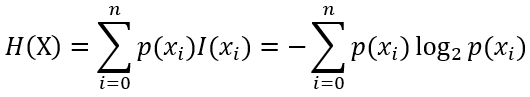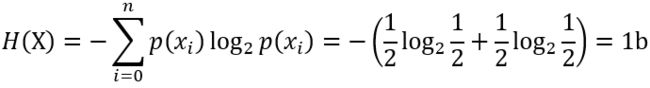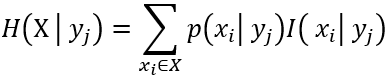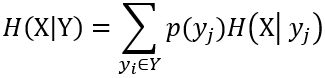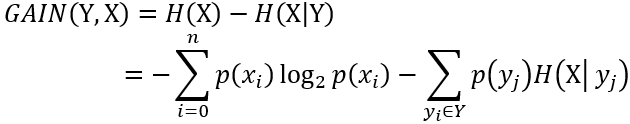目录
一、初识决策树
二、理论基础
三、ID3算法
四、问题实现
五、运行结果分析
六、References
一、初识决策树
决策树（ Decision Tree ）又称为判定树，是对数据进行分类的一种树结构，并通过分类达到预测的目的。决策树分为分类树和回归树两种，分类树是对离散变量做决策树，回归树是对连续变量做决策树。构造决策树是采用自上而下的递归构造方法。
决策树构造的结果是一棵二叉或多叉树，它的输入是一组带有类别标记的训练数据。决策树中的每个内部结点代表对某个属性的一次测试，每条边代表一个测试结果，叶结点代表某个类或者类的分布，最上面的结点是根结点。二叉树的非叶结点一般表示为一个逻辑判断，如形为 （a = b） 的逻辑判断，其中 a 是属性，b 是该属性的某个属性值；树的边是逻辑判断的分支结果；树的叶结点都是类别标记。多叉树的内部结点是属性，边是该属性的所有取值，有几个属性值，就有几条边。
决策树的分类过程也就是决策树分类模型（简称决策树）的生成过程，如下图所示。从图中可知决策树分类的建立过程与用决策树分类模型进行预测的过程实际上是一种归纳-演绎过程。其中，由已分类数据得到决策树分类模型的过程称归纳过程，用决策树分类模型对未分类数据进行分类的过程称为演绎过程。需要强调的是：由训练集得到分类模型必须经过测试集测试达到一定要求才能用于预测。
二、理论基础
1.信息量：衡量信息多少的物理量。
若概率很大，人们事先已有所估计，则该消息信息量很小；若概率很小，人们感到很突然，则该消息所含信息量很大。
信息量的定义：若一个消息x出现的概率为p，则这一消息所含的信息量为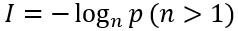
n=2时，单位为bit；n=e时，单位为nat；n=10时，单位为hart。一般计算中n常取2。
例：抛一枚均匀硬币，出现正面和反面的信息量是多少？
解：出现正反面概率均为0.5，则
2.信息熵
信源含有的信息量是信源发出的所有可能消息的平均不确定性，香农把信源所含有的信息量称为信息熵，是指每个属性所含信息量的统计平均值，即所有可能发生事件所带来的的信息量的期望。信息论中一个离散型随机变量X的熵定义如下：
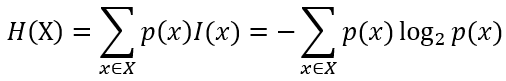
信息熵的定义也可表示为：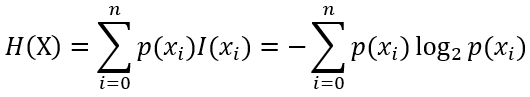
n为训练集X类别数，如子集结果类别为正面、反面，则n为2。
例：抛一枚均匀硬币的信息熵是多少？
解：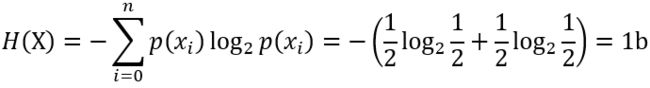
（注：ID3算法中会为每一个类别计算信息熵，具有最小信息熵的类别在本次迭代中用来划分数据集X。）
3.条件自信息量
在事件
出现的条件下，随机事件
发生的条件概率为
，则它的条件自信息量定义为条件概率对数的负值：
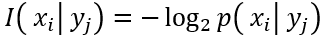
4.条件熵
条件熵的定义是：在Y给定条件下，X的条件概率分布的熵对Y的数学期望。
在给定条件下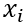，的条件自信息量为
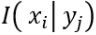，X集合的条件熵为：
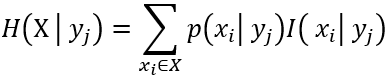
在给定Y（即各个）条件下，X集合的条件熵为：
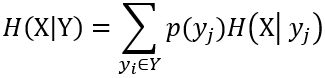
注意：条件熵中Y也是一个变量，意思是在一个变量Y的条件下（变量Y的每个值都会取），另一个变量X熵对Y的期望。条件熵不是指在给定某个数（某个变量为某个值）的情况下，另一个变量的熵是多少，变量的不确定性是多少，而是整体X变量的不确定度或期望！
5.信息增益
信息增益描述了一个特征带来的信息量的多少，往往用于特征选择。一个特征往往会使一个随机变量Y的信息量减少，减少的部分就是信息增益。
信息增益 = 信息熵 - 条件熵
是表示集合X被属性Y分类之前和之后熵的差异。即：集合X原来的熵和已知属性Y之后的熵之差。表示属性Y被固定前后集合X的不确定性降低了多少。
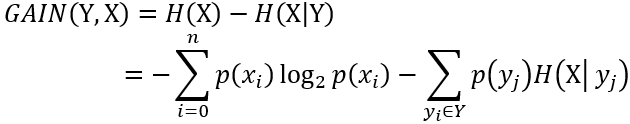
（注：ID3算法中会为每一个类别计算信息熵，具有最大信息增益的类别在本次迭代中用来划分数据集X。）
三、ID3算法
ID3 (Iterative Dichotomiser 3) 是由Quinlan提出的分类预测算法，用来给一个数据集创建决策树。该算法以信息论为基础，以信息熵和信息增益为衡量标准，从而实现对数据的归纳分类。ID3算法计算每个属性的信息增益，并选取具有最高增益的属性作为给定集合的测试属性。对被选取的测试属性创建一个节点，并以该节点的属性标记，对该属性的每个值创建一个分支以此划分样本。
算法流程[References 2]：
四、问题实现
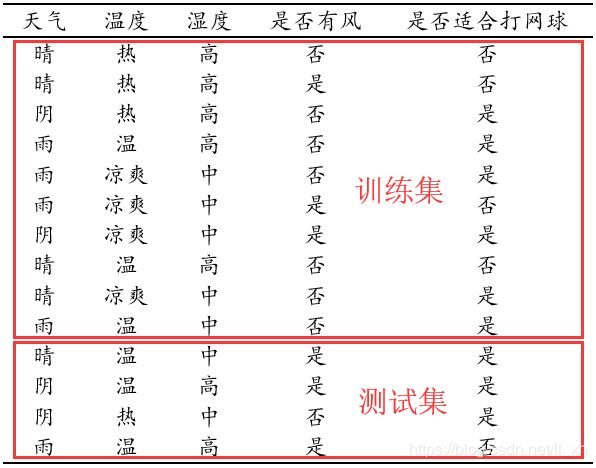
问题描述：给定上述天气数据，将数据划分为训练集和测试集（最后四行），设计算法使用测试集测试构造的决策树，然后使用测试集数据进行预测，看是否适合打网球一栏是否能够正确对应。
程序设计思想（ID3）：每次从数据集中根据最大信息增益选取一个最好特征，将数据进行划分，每次划分都会消耗一个特征，使得特征越来越少，当所有数据集都是同一类，或者消耗完所有特征时，划分结束。其中信息熵和信息增益使用前面理论基础部分的公式。
说明：为了区分最后两列的取值，使观察更方便，我将最后一列中“是”替换为“适合”，“否”替换为“不适合”。
C++实现：代码修改自References[4]
#include
#include
#include
#include
#include
#include
五、运行结果分析
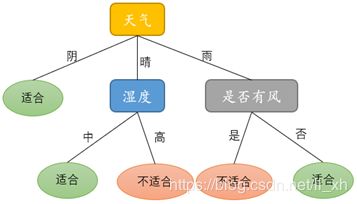
1.根据实现代码打印出根据训练集归纳反演出的决策树如下图：
整理出较为规整的基于ID3算法的决策树如下图：
2. 输入测试集数据可得到以下预测结果
分析上述结果可知，测试集中第一条数据的预测结果与原表不符，说明决策树的预测结果存在误差，原因是训练集太小，需要更多数据加入训练。
经过测试集数据的添加后完善了决策树，得到新的决策树如下图。最终的决策树更加完善，有效降低了预测的错误率。
六、References
[1] https://blog.csdn.net/yijichangkong/article/details/47260847
[2] https://wenku.baidu.com/view/7aa9fbd776eeaeaad1f3305d.html
[3] http://www.dzsc.com/data/2011-8-29/95580.html
[4]https://blog.csdn.net/u012319493/article/details/53112577
