NLP系列(2)_用朴素贝叶斯进行文本分类(上)
作者:龙心尘 && 寒小阳
时间:2016年1月。
出处:
http://blog.csdn.net/longxinchen_ml/article/details/50597149
http://blog.csdn.net/han_xiaoyang/article/details/50616559
声明:版权所有,转载请联系作者并注明出处
##1. 引言
贝叶斯方法是一个历史悠久,有着坚实的理论基础的方法,同时处理很多问题时直接而又高效,很多高级自然语言处理模型也可以从它演化而来。因此,学习贝叶斯方法,是研究自然语言处理问题的一个非常好的切入口。
##2. 贝叶斯公式
贝叶斯公式就一行:
$P(Y|X)=\frac{P(X|Y)P(Y)}{P(X)} $
而它其实是由以下的联合概率公式推导出来:
$P(Y,X) = P(Y|X)P(X)=P(X|Y)P(Y) $
其中 P ( Y ) P(Y) P(Y)叫做先验概率, P ( Y ∣ X ) P(Y|X) P(Y∣X)叫做后验概率, P ( Y , X ) P(Y,X) P(Y,X)叫做联合概率。
额,恩,没了,贝叶斯最核心的公式就这么些。
##3. 用机器学习的视角理解贝叶斯公式
在机器学习的视角下,我们把 X X X理解成**“具有某特征”,把 Y Y Y理解成“类别标签”(一般机器学习问题中都是X=>特征, Y=>结果对吧)。在最简单的二分类问题(是与否判定)下,我们将 Y Y Y理解成“属于某类**”的标签。于是贝叶斯公式就变形成了下面的样子:
$P(“属于某类”|“具有某特征”)=\frac{P(“具有某特征”|“属于某类”)P(“属于某类”)}{P(“具有某特征”)} $
我们尝试更口(shuo)语(ren)化(hua)的方式解释一下上述公式:
P ( “ 属 于 某 类 ” ∣ “ 具 有 某 特 征 ” ) = P(“属于某类”|“具有某特征”)= P(“属于某类”∣“具有某特征”)=在已知某样本“具有某特征”的条件下,该样本“属于某类”的概率。所以叫做**『后验概率』**。
P ( “ 具 有 某 特 征 ” ∣ “ 属 于 某 类 ” ) = P(“具有某特征”|“属于某类”)= P(“具有某特征”∣“属于某类”)=在已知某样本“属于某类”的条件下,该样本“具有某特征”的概率。
P ( “ 属 于 某 类 ” ) = P(“属于某类”) = P(“属于某类”)=(在未知某样本具有该“具有某特征”的条件下,)该样本“属于某类”的概率。所以叫做**『先验概率』**。
P ( “ 具 有 某 特 征 ” ) = P(“具有某特征”) = P(“具有某特征”)=(在未知某样本“属于某类”的条件下,)该样本“具有某特征”的概率。
而我们二分类问题的最终目的就是要判断 P ( “ 属 于 某 类 ” ∣ “ 具 有 某 特 征 ” ) P(“属于某类”|“具有某特征”) P(“属于某类”∣“具有某特征”)是否大于1/2就够了。贝叶斯方法把计算**“具有某特征的条件下属于某类”的概率转换成需要计算“属于某类的条件下具有某特征”**的概率,而后者获取方法就简单多了,我们只需要找到一些包含已知特征标签的样本,即可进行训练。而样本的类别标签都是明确的,所以贝叶斯方法在机器学习里属于有监督学习方法。
这里再补充一下,一般**『先验概率』、『后验概率』是相对**出现的,比如 P ( Y ) P(Y) P(Y)与 P ( Y ∣ X ) P(Y|X) P(Y∣X)是关于 Y Y Y的先验概率与后验概率, P ( X ) P(X) P(X)与 P ( X ∣ Y ) P(X|Y) P(X∣Y)是关于 X X X的先验概率与后验概率。
##4. 垃圾邮件识别
举个例子好啦,我们现在要对邮件进行分类,识别垃圾邮件和普通邮件,如果我们选择使用朴素贝叶斯分类器,那目标就是判断 P ( “ 垃 圾 邮 件 ” ∣ “ 具 有 某 特 征 ” ) P(“垃圾邮件”|“具有某特征”) P(“垃圾邮件”∣“具有某特征”)是否大于1/2。现在假设我们有垃圾邮件和正常邮件各1万封作为训练集。需要判断以下这个邮件是否属于垃圾邮件:
“我司可办理正规发票(保真)17%增值税发票点数优惠!”
也就是判断概率 P ( “ 垃 圾 邮 件 ” ∣ “ 我 司 可 办 理 正 规 发 票 ( 保 真 ) 17 % 增 值 税 发 票 点 数 优 惠 ! ” ) P(“垃圾邮件”|“我司可办理正规发票(保真)17\%增值税发票点数优惠!”) P(“垃圾邮件”∣“我司可办理正规发票(保真)17%增值税发票点数优惠!”)是否大于1/2。
咳咳,有木有发现,转换成的这个概率,计算的方法:就是写个计数器,然后+1 +1 +1统计出所有垃圾邮件和正常邮件中出现这句话的次数啊!!!好,具体点说:
P ( “ 垃 圾 邮 件 ” ∣ “ 我 司 可 办 理 正 规 发 票 ( 保 真 ) 17 % 增 值 税 发 票 点 数 优 惠 ! ” ) P(“垃圾邮件”|“我司可办理正规发票(保真)17\%增值税发票点数优惠!”) P(“垃圾邮件”∣“我司可办理正规发票(保真)17%增值税发票点数优惠!”)
$ =\frac{垃圾邮件中出现这句话的次数}{垃圾邮件中出现这句话的次数+正常邮件中出现这句话的次数}$
##5. 分词
然后同学们开始朝我扔烂白菜和臭鸡蛋,“骗纸!!误人子弟!!你以为发垃圾邮件的人智商都停留在20世纪吗!!你以为它们发邮件像抄作业一样不改内容吗!!哪来那么多相同的句子!!"。
咳咳,表闹,确实,在我们这样的样本容量下,『完全击中』的句子很少甚至没有(无法满足大数定律,),算出来的概率会很失真。一方面找到庞大的训练集是一件非常困难的事情,另一方面其实对于任何的训练集,我们都可以构造出一个从未在训练集中出现的句子作为垃圾邮件(真心的,之前看过朴素贝叶斯分类分错的邮件,我觉得大中华同胞创(zao)新(jia)的能力简直令人惊(fa)呀(zhi))。
一个很悲哀但是很现实的结论:
训练集是有限的,而句子的可能性则是无限的。所以覆盖所有句子可能性的训练集是不存在的。
所以解决方法是?
对啦!句子的可能性无限,但是词语就那么些!!汉语常用字2500个,常用词语也就56000个(你终于明白小学语文老师的用心良苦了)。按人们的经验理解,两句话意思相近并不强求非得每个字、词语都一样。比如“我司可办理正规发票,17%增值税发票点数优惠!”,这句话就比之前那句话少了**“(保真)”**这个词,但是意思基本一样。如果把这些情况也考虑进来,那样本数量就会增加,这就方便我们计算了。
于是,我们可以不拿句子作为特征,而是拿句子里面的词语(组合)作为特征去考虑。比如**“正规发票”可以作为一个单独的词语,“增值税”**也可以作为一个单独的词语等等。
句子**“我司可办理正规发票,17%增值税发票点数优惠!”就可以变成(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”))**。
于是你接触到了中文NLP中,最最最重要的技术之一:分词!!!也就是把一整句话拆分成更细粒度的词语来进行表示。咳咳,另外,分词之后去除标点符号、数字甚至无关成分(停用词)是特征预处理中的一项技术。
中文分词是一个专门的技术领域(我不会告诉你某搜索引擎厂码砖工有专门做分词的!!!),我们将在下一篇文章探讨,这里先将其作为一个已知情况进行处理。具体细节请见下回分晓
我们观察(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”),这可以理解成一个向量:向量的每一维度都表示着该特征词在文本中的特定位置存在。这种将特征拆分成更小的单元,依据这些更灵活、更细粒度的特征进行判断的思维方式,在自然语言处理与机器学习中都是非常常见又有效的。
因此贝叶斯公式就变成了:
P ( “ 垃 圾 邮 件 ” ∣ ( “ 我 ” , “ 司 ” , “ 可 ” , “ 办 理 ” , “ 正 规 发 票 ” , “ 保 真 ” , “ 增 值 税 ” , “ 发 票 ” , “ 点 数 ” , “ 优 惠 ” ) ) P(“垃圾邮件”|(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)) P(“垃圾邮件”∣(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”))
= P ( ( “ 我 ” , “ 司 ” , “ 可 ” , “ 办 理 ” , “ 正 规 发 票 ” , “ 保 真 ” , “ 增 值 税 ” , “ 发 票 ” , “ 点 数 ” , “ 优 惠 ” ) ∣ " 垃 圾 邮 件 " ) P ( “ 垃 圾 邮 件 ” ) P ( ( “ 我 ” , “ 司 ” , “ 可 ” , “ 办 理 ” , “ 正 规 发 票 ” , “ 保 真 ” , “ 增 值 税 ” , “ 发 票 ” , “ 点 数 ” , “ 优 惠 ” ) ) =\frac{P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)|"垃圾邮件")P(“垃圾邮件”)}{P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)) } =P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”))P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)∣"垃圾邮件")P(“垃圾邮件”)
P ( “ 正 常 邮 件 ” ∣ ( “ 我 ” , “ 司 ” , “ 可 ” , “ 办 理 ” , “ 正 规 发 票 ” , “ 保 真 ” , “ 增 值 税 ” , “ 发 票 ” , “ 点 数 ” , “ 优 惠 ” ) ) P(“正常邮件”|(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)) P(“正常邮件”∣(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”))
= P ( ( “ 我 ” , “ 司 ” , “ 可 ” , “ 办 理 ” , “ 正 规 发 票 ” , “ 保 真 ” , “ 增 值 税 ” , “ 发 票 ” , “ 点 数 ” , “ 优 惠 ” ) ∣ " 正 常 邮 件 " ) P ( “ 正 常 邮 件 ” ) P ( ( “ 我 ” , “ 司 ” , “ 可 ” , “ 办 理 ” , “ 正 规 发 票 ” , “ 保 真 ” , “ 增 值 税 ” , “ 发 票 ” , “ 点 数 ” , “ 优 惠 ” ) ) =\frac{P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)|"正常邮件")P(“正常邮件”)}{P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)) } =P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”))P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)∣"正常邮件")P(“正常邮件”)
##6. 条件独立假设
有些同学说…好像…似乎…经过上面折腾,概率看起来更复杂了-_-||
那…那我们简化一下…
概率 P ( ( “ 我 ” , “ 司 ” , “ 可 ” , “ 办 理 ” , “ 正 规 发 票 ” , “ 保 真 ” , “ 增 值 税 ” , “ 发 票 ” , “ 点 数 ” , “ 优 惠 ” ) ∣ " 垃 圾 邮 件 " ) P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)|"垃圾邮件") P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)∣"垃圾邮件")依旧不够好求,我们引进一个很朴素的近似。为了让公式显得更加紧凑,我们令字母S表示“垃圾邮件”,令字母H表示“正常邮件”。近似公式如下:
P ( ( “ 我 ” , “ 司 ” , “ 可 ” , “ 办 理 ” , “ 正 规 发 票 ” , “ 保 真 ” , “ 增 值 税 ” , “ 发 票 ” , “ 点 数 ” , “ 优 惠 ” ) ∣ S ) P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)|S) P((“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)∣S)
= P ( “ 我 ” ∣ S ) × P ( “ 司 ” ∣ S ) × P ( “ 可 ” ∣ S ) × P ( “ 办 理 ” ∣ S ) × P ( “ 正 规 发 票 ” ∣ S ) =P(“我”|S)×P(“司”|S)×P(“可”|S)×P(“办理”|S)×P(“正规发票”|S) =P(“我”∣S)×P(“司”∣S)×P(“可”∣S)×P(“办理”∣S)×P(“正规发票”∣S)
× P ( “ 保 真 ” ∣ S ) × P ( “ 增 值 税 ” ∣ S ) × P ( “ 发 票 ” ∣ S ) × P ( “ 点 数 ” ∣ S ) × P ( “ 优 惠 ” ∣ S ) ×P(“保真”|S)×P(“增值税”|S)×P(“发票”|S)×P(“点数”|S)×P(“优惠”|S) ×P(“保真”∣S)×P(“增值税”∣S)×P(“发票”∣S)×P(“点数”∣S)×P(“优惠”∣S)
这就是传说中的条件独立假设。基于“正常邮件”的条件独立假设的式子与上式类似,此处省去。接着,将条件独立假设代入上面两个相反事件的贝叶斯公式。
于是我们就只需要比较以下两个式子的大小:
C = P ( “ 我 ” ∣ S ) P ( “ 司 ” ∣ S ) P ( “ 可 ” ∣ S ) P ( “ 办 理 ” ∣ S ) P ( “ 正 规 发 票 ” ∣ S ) C = P(“我”|S)P(“司”|S)P(“可”|S)P(“办理”|S)P(“正规发票”|S) C=P(“我”∣S)P(“司”∣S)P(“可”∣S)P(“办理”∣S)P(“正规发票”∣S)
× P ( “ 保 真 ” ∣ S ) P ( “ 增 值 税 ” ∣ S ) P ( “ 发 票 ” ∣ S ) P ( “ 点 数 ” ∣ S ) P ( “ 优 惠 ” ∣ S ) P ( “ 垃 圾 邮 件 ” ) ×P(“保真”|S)P(“增值税”|S)P(“发票”|S)P(“点数”|S)P(“优惠”|S)P(“垃圾邮件”) ×P(“保真”∣S)P(“增值税”∣S)P(“发票”∣S)P(“点数”∣S)P(“优惠”∣S)P(“垃圾邮件”)
C ‾ = P ( “ 我 ” ∣ H ) P ( “ 司 ” ∣ H ) P ( “ 可 ” ∣ H ) P ( “ 办 理 ” ∣ H ) P ( “ 正 规 发 票 ” ∣ H ) \overline{C}=P(“我”|H)P(“司”|H)P(“可”|H)P(“办理”|H)P(“正规发票”|H) C=P(“我”∣H)P(“司”∣H)P(“可”∣H)P(“办理”∣H)P(“正规发票”∣H)
$×P(“保真”|H)P(“增值税”|H)P(“发票”|H)P(“点数”|H)P(“优惠”|H)P(“正常邮件”) $
厉(wo)害(cao)!酱紫处理后式子中的每一项都特别好求!只需要分别统计各类邮件中该关键词出现的概率就可以了!!!比如:
P ( “ 发 票 ” ∣ S ) = 垃 圾 邮 件 中 所 有 “ 发 票 ” 的 次 数 垃 圾 邮 件 中 所 有 词 语 的 次 数 P(“发票”|S)=\frac{垃圾邮件中所有“发票”的次数}{垃圾邮件中所有词语的次数} P(“发票”∣S)=垃圾邮件中所有词语的次数垃圾邮件中所有“发票”的次数
统计次数非常方便,而且样本数量足够大,算出来的概率比较接近真实。于是垃圾邮件识别的问题就可解了。
##7. 朴素贝叶斯(Naive Bayes),“Naive”在何处?
加上条件独立假设的贝叶斯方法就是朴素贝叶斯方法(Naive Bayes)。 Naive的发音是“乃一污”,意思是“朴素的”、“幼稚的”、“蠢蠢的”。咳咳,也就是说,大神们取名说该方法是一种比较萌蠢的方法,为啥?
将句子(“我”,“司”,“可”,“办理”,“正规发票”) 中的 (“我”,“司”)与(“正规发票”)调换一下顺序,就变成了一个新的句子(“正规发票”,“可”,“办理”, “我”, “司”)。新句子与旧句子的意思完全不同。**但由于乘法交换律,朴素贝叶斯方法中算出来二者的条件概率完全一样!**计算过程如下:
P ( ( “ 我 ” , “ 司 ” , “ 可 ” , “ 办 理 ” , “ 正 规 发 票 ” ) ∣ S ) P((“我”,“司”,“可”,“办理”,“正规发票”)|S) P((“我”,“司”,“可”,“办理”,“正规发票”)∣S)
$=P(“我”|S)P(“司”|S)P(“可”|S)P(“办理”|S)P(“正规发票”|S) $
= P ( “ 正 规 发 票 ” ∣ S ) P ( “ 可 ” ∣ S ) P ( “ 办 理 ” ∣ S ) P ( “ 我 ” ∣ S ) P ( “ 司 ” ∣ S ) =P(“正规发票”|S)P(“可”|S)P(“办理”|S)P(“我”|S)P(“司”|S) =P(“正规发票”∣S)P(“可”∣S)P(“办理”∣S)P(“我”∣S)P(“司”∣S)
= P ( ( “ 正 规 发 票 ” , “ 可 ” , “ 办 理 ” , “ 我 ” , “ 司 ” ) ∣ S ) =P((“正规发票”,“可”,“办理”, “我”, “司”)|S) =P((“正规发票”,“可”,“办理”,“我”,“司”)∣S)
也就是说,在朴素贝叶斯眼里,“我司可办理正规发票”与“正规发票可办理我司”完全相同。朴素贝叶斯失去了词语之间的顺序信息。这就相当于把所有的词汇扔进到一个袋子里随便搅和,贝叶斯都认为它们一样。因此这种情况也称作词袋子模型(bag of words)。
词袋子模型与人们的日常经验完全不同。比如,在条件独立假设的情况下,**“武松打死了老虎”与“老虎打死了武松”被它认作一个意思了。**恩,朴素贝叶斯就是这么单纯和直接,对比于其他分类器,好像是显得有那么点萌蠢。
##8. 简单高效,吊丝逆袭
虽然说朴素贝叶斯方法萌蠢萌蠢的,但实践证明在垃圾邮件识别的应用还令人诧异地好。Paul Graham先生自己简单做了一个朴素贝叶斯分类器,“1000封垃圾邮件能够被过滤掉995封,并且没有一个误判”。(Paul Graham《黑客与画家》)
那个…效果为啥好呢?
“有人对此提出了一个理论解释,并且建立了什么时候朴素贝叶斯的效果能够等价于非朴素贝叶斯的充要条件,这个解释的核心就是:有些独立假设在各个分类之间的分布都是均匀的所以对于似然的相对大小不产生影响;即便不是如此,也有很大的可能性各个独立假设所产生的消极影响或积极影响互相抵消,最终导致结果受到的影响不大。具体的数学公式请参考这篇 paper。”(刘未鹏《:平凡而又神奇的贝叶斯方法》)
恩,这个分类器中最简单直接看似萌蠢的小盆友『朴素贝叶斯』,实际上却是简单、实用、且强大的。
9. 处理重复词语的三种方式
我们**之前的垃圾邮件向量(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”),其中每个词都不重复。**而这在现实中其实很少见。因为如果文本长度增加,或者分词方法改变,必然会有许多词重复出现,因此需要对这种情况进行进一步探讨。比如以下这段邮件:
“代开发票。增值税发票,正规发票。”
分词后为向量:
(“代开”,“发票”,“增值税”,“发票”,“正规”,“发票”)
其中“发票”重复了三次。
9.1 多项式模型:
如果我们考虑重复词语的情况,也就是说,重复的词语我们视为其出现多次,直接按条件独立假设的方式推导,则有
P ( ( “ 代 开 ” , “ 发 票 ” , “ 增 值 税 ” , “ 发 票 ” , “ 正 规 ” , “ 发 票 ” ) ∣ S ) P((“代开”,“发票”,“增值税”,“发票”,“正规”,“发票”)|S) P((“代开”,“发票”,“增值税”,“发票”,“正规”,“发票”)∣S)
= P ( “ 代 开 ” ” ∣ S ) P ( “ 发 票 ” ∣ S ) P ( “ 增 值 税 ” ∣ S ) P ( “ 发 票 ” ∣ S ) P ( “ 正 规 ” ∣ S ) P ( “ 发 票 ” ∣ S ) =P(“代开””|S)P(“发票”|S)P(“增值税”|S)P(“发票”|S)P(“正规”|S)P(“发票”|S) =P(“代开””∣S)P(“发票”∣S)P(“增值税”∣S)P(“发票”∣S)P(“正规”∣S)P(“发票”∣S)
= P ( “ 代 开 ” ” ∣ S ) P 3 ( “ 发 票 ” ∣ S ) P ( “ 增 值 税 ” ∣ S ) P ( “ 正 规 ” ∣ S ) =P(“代开””|S)P^3(“发票”|S)P(“增值税”|S)P(“正规”|S) =P(“代开””∣S)P3(“发票”∣S)P(“增值税”∣S)P(“正规”∣S)
注意这一项: P 3 ( “ 发 票 ” ∣ S ) P^3(“发票”|S) P3(“发票”∣S)。
在统计计算P(“发票”|S)时,每个被统计的垃圾邮件样本中重复的词语也统计多次。
P ( “ 发 票 ” ∣ S ) = 每 封 垃 圾 邮 件 中 出 现 “ 发 票 ” 的 次 数 的 总 和 每 封 垃 圾 邮 件 中 所 有 词 出 现 次 数 ( 计 算 重 复 次 数 ) 的 总 和 P(“发票”|S)=\frac{每封垃圾邮件中出现“发票”的次数的总和}{每封垃圾邮件中所有词出现次数(计算重复次数)的总和} P(“发票”∣S)=每封垃圾邮件中所有词出现次数(计算重复次数)的总和每封垃圾邮件中出现“发票”的次数的总和
你看这个多次出现的结果,出现在概率的指数/次方上,因此这样的模型叫作多项式模型。
9.2 伯努利模型
另一种更加简化的方法是将重复的词语都视为其只出现1次,
P ( ( “ 代 开 ” , “ 发 票 ” , “ 增 值 税 ” , “ 发 票 ” , “ 正 规 ” , “ 发 票 ” ) ∣ S ) P((“代开”,“发票”,“增值税”,“发票”,“正规”,“发票”)|S) P((“代开”,“发票”,“增值税”,“发票”,“正规”,“发票”)∣S)
= P ( “ 发 票 ” ∣ S ) P ( “ 代 开 ” ” ∣ S ) P ( “ 增 值 税 ” ∣ S ) P ( “ 正 规 ” ∣ S ) =P(“发票”|S)P(“代开””|S)P(“增值税”|S)P(“正规”|S) =P(“发票”∣S)P(“代开””∣S)P(“增值税”∣S)P(“正规”∣S)
统计计算 P ( “ 词 语 ” ∣ S ) P(“词语”|S) P(“词语”∣S)时也是如此。
P ( “ 发 票 ” ∣ S ) = 出 现 “ 发 票 ” 的 垃 圾 邮 件 的 封 数 每 封 垃 圾 邮 件 中 所 有 词 出 现 次 数 ( 出 现 了 只 计 算 一 次 ) 的 总 和 P(“发票”|S)=\frac{出现“发票”的垃圾邮件的封数}{每封垃圾邮件中所有词出现次数(出现了只计算一次)的总和} P(“发票”∣S)=每封垃圾邮件中所有词出现次数(出现了只计算一次)的总和出现“发票”的垃圾邮件的封数
这样的模型叫作伯努利模型(又称为二项独立模型)。这种方式更加简化与方便。当然它丢失了词频的信息,因此效果可能会差一些。
9.3 混合模型
第三种方式是在计算句子概率时,不考虑重复词语出现的次数,但是在统计计算词语的概率P(“词语”|S)时,却考虑重复词语的出现次数,这样的模型可以叫作混合模型。
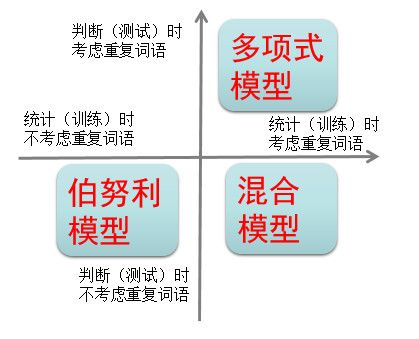
我们通过下图展示三种模型的关系。
实践中采用哪种模型,关键看具体的业务场景。笔者的简单经验是,对于垃圾邮件识别,混合模型更好些。
10. 去除停用词与选择关键词
我们继续观察**(“我”,“司”,“可”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)** 这句话。其实,像**“我”、“可”之类词其实非常中性,无论其是否出现在垃圾邮件中都无法帮助判断的有用信息。所以可以直接不考虑这些典型的词。这些无助于我们分类的词语叫作“停用词”(Stop Words)。这样可以减少我们训练模型、判断分类的时间**。
于是之前的句子就变成了**(“司”,“办理”,“正规发票”,“保真”,“增值税”,“发票”,“点数”,“优惠”)** 。
我们进一步分析。以人类的经验,其实**“正规发票”、“发票”这类的词如果出现的话,邮件作为垃圾邮件的概率非常大,可以作为我们区分垃圾邮件的“关键词”。而像“司”、“办理”、“优惠”这类的词则有点鸡肋,可能有助于分类,但又不那么强烈。如果想省事做个简单的分类器的话,则可以直接采用“关键词”进行统计与判断,剩下的词就可以先不管了。于是之前的垃圾邮件句子就变成了(“正规发票”,“发票”)** 。这样就更加减少了我们训练模型、判断分类的时间,速度非常快。
“停用词”和“关键词”一般都可以提前靠人工经验指定。不同的“停用词”和“关键词”训练出来的分类器的效果也会有些差异。那么有没有量化的指标来评估不同词语的区分能力?在我们之前的文章《机器学习系列(6)_从白富美相亲看特征选择与预处理(下)》其实就提供了一种评价方法,大家可以参考。此处就不赘述了。
11. 浅谈平滑技术
我们来说个问题(中文NLP里问题超级多,哭瞎T_T),比如在计算以下独立条件假设的概率:
P ( ( “ 我 ” , “ 司 ” , “ 可 ” , “ 办 理 ” , “ 正 规 发 票 ” ) ∣ S ) P((“我”,“司”,“可”,“办理”,“正规发票”)|S) P((“我”,“司”,“可”,“办理”,“正规发票”)∣S)
= P ( “ 我 ” ∣ S ) P ( “ 司 ” ∣ S ) P ( “ 可 ” ∣ S ) P ( “ 办 理 ” ∣ S ) P ( “ 正 规 发 票 ” ∣ S ) =P(“我”|S)P(“司”|S)P(“可”|S)P(“办理”|S)P(“正规发票”|S) =P(“我”∣S)P(“司”∣S)P(“可”∣S)P(“办理”∣S)P(“正规发票”∣S)
我们扫描一下训练集,发现**“正规发票”这个词从出现过!!!,于是 P ( “ 正 规 发 票 ” ∣ S ) = 0 P(“正规发票”|S)=0 P(“正规发票”∣S)=0…问题严重了,整个概率都变成0了!!!朴素贝叶斯方法面对一堆0,很凄惨地失效了…更残酷的是这种情况其实很常见**,因为哪怕训练集再大,也可能有覆盖不到的词语。本质上还是样本数量太少,不满足大数定律,计算出来的概率失真。为了解决这样的问题,一种分析思路就是直接不考虑这样的词语,但这种方法就相当于默认给P(“正规发票”|S)赋值为1。其实效果不太好,大量的统计信息给浪费掉了。我们进一步分析,既然可以默认赋值为1,为什么不能默认赋值为一个很小的数?这就是平滑技术的基本思路,依旧保持着一贯的作风,朴实/土但是直接而有效。
对于伯努利模型,P(“正规发票”|S)的一种平滑算法是:
P ( “ 正 规 发 票 ” ∣ S ) = 出 现 “ 正 规 发 票 ” 的 垃 圾 邮 件 的 封 数 + 1 每 封 垃 圾 邮 件 中 所 有 词 出 现 次 数 ( 出 现 了 只 计 算 一 次 ) 的 总 和 + 2 P(“正规发票”|S)=\frac{出现“正规发票”的垃圾邮件的封数+1}{每封垃圾邮件中所有词出现次数(出现了只计算一次)的总和+2} P(“正规发票”∣S)=每封垃圾邮件中所有词出现次数(出现了只计算一次)的总和+2出现“正规发票”的垃圾邮件的封数+1
对于多项式模型,P(“正规发票”| S)的一种平滑算法是:
P ( “ 发 票 ” ∣ S ) = 每 封 垃 圾 邮 件 中 出 现 “ 发 票 ” 的 次 数 的 总 和 + 1 每 封 垃 圾 邮 件 中 所 有 词 出 现 次 数 ( 计 算 重 复 次 数 ) 的 总 和 + 被 统 计 的 词 表 的 词 语 数 量 P(“发票”|S)=\frac{每封垃圾邮件中出现“发票”的次数的总和+1}{每封垃圾邮件中所有词出现次数(计算重复次数)的总和+被统计的词表的词语数量} P(“发票”∣S)=每封垃圾邮件中所有词出现次数(计算重复次数)的总和+被统计的词表的词语数量每封垃圾邮件中出现“发票”的次数的总和+1
说起来,平滑技术的种类其实非常多,有兴趣的话回头我们专门拉个专题讲讲好了。这里只提一点,就是所有的平滑技术都是给未出现在训练集中的词语一个估计的概率,而相应地调低其他已经出现的词语的概率。
平滑技术是因为数据集太小而产生的现实需求。如果数据集足够大,平滑技术对结果的影响将会变小。
12. 小结
我们找了个最简单常见的例子:垃圾邮件识别,说明了一下朴素贝叶斯进行文本分类的思路过程。基本思路是先区分好训练集与测试集,对文本集合进行分词、去除标点符号等特征预处理的操作,然后使用条件独立假设,将原概率转换成词概率乘积,再进行后续的处理。
贝叶斯公式 + 条件独立假设 = 朴素贝叶斯方法
基于对重复词语在训练阶段与判断(测试)阶段的三种不同处理方式,我们相应的有伯努利模型、多项式模型和混合模型。在训练阶段,如果样本集合太小导致某些词语并未出现,我们可以采用平滑技术对其概率给一个估计值。而且并不是所有的词语都需要统计,我们可以按相应的“停用词”和“关键词”对模型进行进一步简化,提高训练和判断速度。
因为公式比较多,为了防止看到公式就狗带的情况,我们尽量用口(shuo)语(ren)化(hua)的方式表达公式,不严谨之处还望见谅,有纰漏之处欢迎大家指出。