文献阅读笔记：XLNet: Generalized Autoregressive Pretraining for Language Understanding

0.背景

机构：谷歌大脑、CMU
作者：Zhilin Yang、Zihang Dai
发布地方：arxiv
面向任务：Language Understanding
论文地址：https://arxiv.org/abs/1904.09482
论文代码：https://github.com/zihangdai/xlnet

0-1. 摘要

由于上下文双向建模的表达能力更强，降噪自编码类型中的典型代表BERT能够比自回归语言模型取得更好的结果。即，上下文建模获得双向的信息在Language Understanding中是很重要的。但是BERT存在以下不足：
(1)在输入端依赖mask的掩模的方式，遮蔽部分的输入信息
(2)忽略了被mask位置之间的依赖性
这两点在预训练-微调两个阶段存在不符。即，上述2个方面在预训练和微调这2个阶段之间都是有差异的。
在正视了上述优缺点之后，本文提出一种通用（或者广义，英语原文是generalized）的自回归预训练方法：XLNet。XLNet的贡献在于
(1)新的双向上下文学习方法：分解输入的顺序，对其进行排列组合，并遍历所有的排列组合，获得最大似然期望。
(2)克服BERT自回归中的缺陷
XLNet在预训练中融合Transformer-XL和state-of-the-art自回归模型的优点。实验结果：XLNet在20个任务中超出了BERT，且很多是碾压式地超越。XLNet在其中18个任务中取得了目前最优结果，包括问答、自然语言推理、情感分析和文档排序。

1. 介绍

预训练+微调的NLP处理方案日渐成为主流，其中预训练阶段根据预训练目标的不同可以分为2种：自回归的语言模型（autoregressive,AR）和自动编码（autoencoding，AE）模型。
AR语言模型就是我们常见的语言模型，采用自回归模型估计一个文本语料的概率分布。其中包括从左到右的文本序列的条件概率和从右往左的序列条件概率。由此可以看出AR模型对于文本都是进行单向编码的，要么是从左往右，要么从右往左，这不能有效地对深层双向上下文进行建模。而下游的language understanding 任务常常需要双向的上下文信息。

基于AE的预训练方法没有进行明确的密度估计，而是致力于从corrupted input中重建出原始的输入数据。其中一个显著的代表是BERT，BERT采用特定标识符[MASK]将输入的token序列进行特定的遮蔽操作。再训练模型从被遮蔽的输入序列(corrupted data)中恢复出原始的tokens。由于其目标不是进行密度估计，所以BERT可以利用文本的双向上下文信息进行输入的重建。这就弥补了上述AR语言建模中的双向信息鸿沟。从而提升结果性能指标。但是在BERT的预训练阶段中人为设定符号[MASK]，会使其与真实场景中的微调数据存在出入。导致预训练-微调的不一致。此外，由于预测的token是输入中被masked的token，BERT不能够像AR语言模型中使用点乘的联合概率。换一句话说，BERT假设待预测的tokens之间是相互独立的，这被过于简化为自然语言中普遍存在的高阶、长程依赖关系。

本文提出的XLNet是一种通用的自回归方法，该方法充分利用了AR语言建模和AE的优点，同时避免了它们的局限性。

• 不再如传统AR模型中那般使用前向或者反向的固定次序作为输入，XLNet最大化输入序列的全部排序组合的似然期望。由于采用排序组合的方式，每个位置的上下文可以由来自左边和右边的token组成。在期望中，每个位置都要学会利用来自所有位置的上下文信息，即，捕获双向上下文信息。

• 作为一个通用的AR语言模型，XLNet不再使用data corruption,即不再使用特定标识符号[MASK]。因此也就不存在BERT中的预训练和微调的不一致性。同时，自回归在分解预测tokens的联合概率时候天然地使用乘法法则，这消除了BERT中的独立性假设。

除了提出一个新的预训练目标，XLNet还改善了预训练的框架设计：

• 受AR语言模型的最新进展启发，XLNet在预训练中借鉴了Transformer-XL中的segment recurrence机制和的相对编码方案。其性能提升在长文本序列上尤为显著。

• 在基于排列组合的语言建模中单纯地使用Transformer-XL框架是无法工作的，这是由于分解后次序是任意的，而target是不明确的。所以，本文提出采用重置Transformer-XL网络（reparameterize the Transformer(-XL) network）以消除上述的不确定性。

相关工作：
排序组合的自回归模型先哲们已经提出[32,11]，本文所不同的在以下几点：
(1)此前的模型是无序的，但是XLNet本质上是有序的，因为其带有位置编码信息。这对于语言理解是至关重要的，否则无序模型直接退化为词袋模型，从而缺乏基本的表达能力。
(2)动机不同。之前的模型致力于通过在模型中引入“无序”诱导偏差来改进密度估计。但是XLNet的动机是使得自回归语言模型能够习得双向的上下文信息。

2. 方法

2.1 背景

先对比传统的自回归语言模型和BERT。对于给定的文本序列$x=[x_1,...,x_T]$，AR语言模型：
$$\underset{\theta }{\max }\log p_{\theta }(\mathbf{x})=\sum _{t=1}^T\log p_{\theta }(x_t|{\mathbf{x}}_{<t})=\sum _{t=1}^T\log \frac{\exp (h_{\theta }({\mathbf{x}}_{1:t-1}{)}^{\top }e(x_t))}{{\sum }_{x^{\prime }}\exp (h_{\theta }({\mathbf{x}}_{1:t-1}{)}^{\top }e(x^{\prime }))}\text{\hspace{1em}(1)}$$
其中$h$是神经网络模型所产生的上下文表征，如RNN或者Transformers。$e(x)$表示$x$的词嵌入。
BERT是基于降噪自编码，对于一个输入$x$，先在一定位置（比如15%）随机地用特定符号[MASK]替代原始tokens，从而得到corrupted version的输入$\hat{x}$。被遮蔽掉的tokens记为$\overline{x}$，训练的目标是从$\hat{x}$重建出$\overline{x}$：
$$\underset{\theta }{\max }\log p_{\theta }(\overline{\mathbf{x}}|\hat{\mathbf{x}})\approx \sum _{t=1}^T{m}_t\log p_{\theta }(x_t|\hat{\mathbf{x}})=\sum _{t=1}^T{m}_t\log \frac{\exp (H_{\theta }(\hat{\mathbf{x}}{)}_t^{\top }e(x_t))}{{\sum }_{x^{\prime }}\exp (H_{\theta }(\hat{\mathbf{x}}{)}_t^{\top }e(x^{\prime }))}\text{\hspace{1em}(2)}$$

其中$m_t=1$表示$x_t$被masked，$H_{\theta }$表示将长度为T的文本序列通过Transformer映射为特征向量：$H_{\theta }(\mathbf{x})=\left[H_{\theta }(\mathbf{x}{)}_1,H_{\theta }(\mathbf{x}{)}_2,\cdots ,H_{\theta }(\mathbf{x}{)}_T\right]$。上述两种预训练目标的优缺点对比如下：

• 独立性假设：注意上述方程(2)中采用的是约等号。BERT假设所有被masked tokens之间是独立的，可以分别独立地重建，据此将条件概率$p(\overline{x}|\hat{x})$进行分解。自回归语言模型的目标分解$p_{\theta }(x)$则是采用乘法法则。这在没有独立假设的情况下普遍成立。

• 输入干扰：BERT的输入包含人为设定的符号如[MASK]，而这些符号在真实的下游任务中是不会出现的。这就使得预训练与微调这两个阶段存在不一致。BERT的原始论文也没有解决该问题，原始的tokens只会以一个很小的概率被使用到，否则方程(2)的优化将微不足道。相比较而言，自回归语言模型不依赖于任何输入上的corruption，自然也就不存在预训练和微调不一致的问题。

• 上下文依赖：自回归模型对于t位置的预测仅仅依赖于t-1位置之前的资讯(从左到右)。但是BERT可以从双向获得表征信息。所以，BERT可以使得模在预训练阶段型捕获到双向的上下文信息。

2.2 目标：排列组合语言模型

对比上述的2种预训练目标，那么是否存在一种预训练目标包含上述二者的优点，且能够避免其不足？受无序NADE[32]的想法的启发，本文提出一个排列组合语言模型，该模型能够保留自回归模型的优点，同时能够捕获双向的上下文信息。一个长度为T的序列，其排序组合为T!直观上，如果所有排列组合次序的参数共享，那么模型应该会从左右两个方向的所有位置收集到信息。

假设$Z_T$表示长度为T序列的所有可能的排序组合。本文提出的排列组合语言模型的目标是：
$$\underset{\theta }{\max }{\mathbb{E}}_{\mathbf{z}\sim {\mathcal{Z}}_T}\left[\sum _{t=1}^T\log p_{\theta }\left(x_{z_t}|{\mathbf{x}}_{{\mathbf{z}}_{<t}}\right)\right]\text{\hspace{1em}(3)}$$
如此$x_t$可以看到其他所有位置的信息，即可以捕获双向的上下文信息。在自回归模型中引入该目标，则可以避免独立性假设和预训练-微调不一致问题。

Remark on Permutation：
所提出的目标仅仅排列分解的次序，而不是序列的顺序。换一句话说，我们依然保持序列的原始顺序不变，而采用与原始序列对应的位置编码，再在Transformer中采用一个attention mask以获得分解次序（factorization order）的排列组合。注意：这个选择是必要的，因为模型只会在finetuning过程中遇到具有自然顺序的文本序列。

Figure1为一个例子，其中token $x_3$是待预测的，对于输入序列x的不同排列组合：

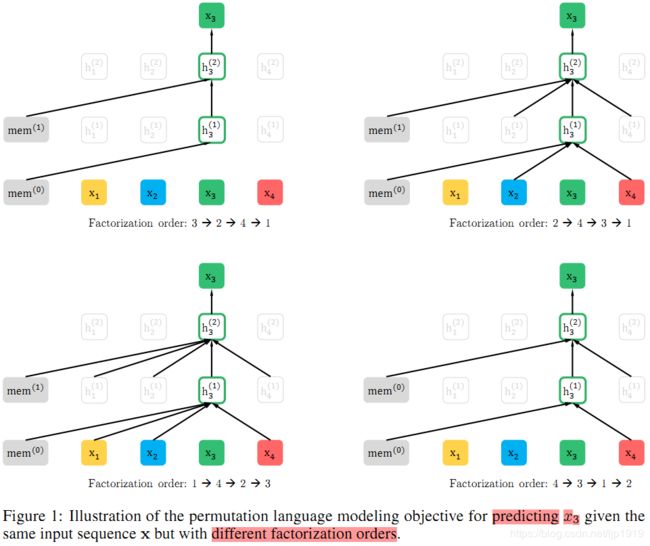
第1种，3->2->4->1。3的前面是mem。
第2种，2->4->3->1。3的前面是2和4，此外还有mem。所以只需要对这些进行attention即可。其他的排序组合同理。
如果将1，2，3，4打乱为3->2->4->1，再采用自回归模型的话，则优化的似然函数为：
$P(x)=P(x_1|x_3,x_2,x_4)\times P(x_4|x_3,x_2)\times P(x_2|x_3)\times P(x_3)$
由于是多种排序组合的模型参数共享，所以模型最终可以学习到所有位置的信息。

2.3 架构：基于双流自注意力机制的Target-Aware Representations

由于排序组合语言模型目标有其期望的性质，如果单纯地使用标准Transformer进行参数化可能是无法工作的。假设参数化下一个token的分布为$p_{\theta }\left(X_{z_t}|{\mathbf{x}}_{{\mathbf{z}}_{<t}}\right)$，当使用标准softmax的话，则结果为：$p_{\theta }(X_{z_t}=x|{\mathbf{x}}_{\mathbf{z}<t})=\frac{\exp \left(e(x{)}^{\top }{h}_{\theta }\left({\mathbf{x}}_z<t\right)\right)}{{\sum }_{x^{\prime }}\exp \left(e{\left(x^{\prime }\right)}^{\top }{h}_{\theta }\left({\mathbf{x}}_z<t\right)\right)}$，其中$h_{\theta }\left({\mathbf{x}}_{\mathbf{z}<t}\right)$表示${\mathbf{X}}_{\mathbf{Z}<t}$的隐含表征，该隐含表征是共享的Transformer网络在使用合适的masking之后生成的。注意：$h_{\theta }\left({\mathbf{x}}_{{\mathbf{z}}_{<t}}\right)$并不依赖于位置信息，即$z_t$。因此，无视target的位置信息，对于相同的分布进行预测是难以学习到有用的表征的(具体参考附录A中的实例)。为避免这个问题，本文提出一个考虑target位置信息的重置参数的next token分布：
$$p_{\theta }\left(X_{z_t}=x|{\mathbf{x}}_{z_{<t}}\right)=\frac{\exp \left(e(x{)}^{\top }{g}_{\theta }\left({\mathbf{x}}_{{\mathbf{z}}_{<t}},z_t\right)\right)}{{\sum }_{x^{\prime }}\exp \left(e{\left(x^{\prime }\right)}^{\top }{g}_{\theta }\left({\mathbf{x}}_{{\mathbf{z}}_{<t}},z_t\right)\right)}\text{\hspace{1em}(4)}$$
其中$g_{\theta }\left({\mathbf{x}}_{\mathbf{z}<t},z_t\right)$表示新的参数化形式，可以看出该参数化形式考虑进了位置信息$z_t$。

这里进一步解释下。比如上面打乱顺序后有一个很大的问题，比如将1，2，3，4打乱为3->2->4->1。就是在预测第三个x的时候模型预测的是$P(x_4|x_3,x_2)$，如果把排列方式换成3->2->1->4，则应该预测$P(x_1|x_3,x_2)$ ，但模型不知道当前要预测的是哪一个。所以说要加入位置信息，即$P(x_4|x_3,x_2,4)$和 $P(x_1|x_3,x_2,1)$ ，让模型知道目前是预测哪个位置的token。具体的例子可以参考附录A。

双流注意力：
那下一个问题又来了，传统的attention只带有token编码，位置信息都在编码里了，而自回归目标是不允许模型看到当前token编码的，因此要把position embedding拆出来。怎么拆呢？本文就提出了Two-Stream Self-Attention。

虽然上述的target-ware representations可以弥补target预测时候的不确定，但是如何构造$g_{\theta }\left({\mathbf{x}}_{{\mathbf{z}}_{<t}},z_t\right)$仍然是一个问题。本文提出固定target位置$z_t$，并通过attention收集位置$z_t$的上下文${\mathbf{X}}_{{\mathbf{z}}_{<t}}$信息。为了使得上述的参数化可以工作，标准 Transformer架构存在两个互相矛盾地方：
(1)预测 token $x_{z_t}$时，$g_{\theta }\left({\mathbf{x}}_{{\mathbf{z}}_{<t}},z_t\right)$应该仅使用位置$z_t$而不是内容$x_{z_t}$，不然该目标函数就变得不重要了。
(2)为了预测另一个 token $x_{z_j}$，其中 j>t，$g_{\theta }\left({\mathbf{x}}_{{\mathbf{z}}_{<t}},z_t\right)$应该编码内容$x_{z<t}$，以提供完整的上下文信息。为了解决这一矛盾，本文提出使用两个隐藏表征，而不是只用其中一个，即双流注意力机制。

• content representation(内容表征)$g_{\theta }\left({\mathbf{x}}_{{\mathbf{z}}_{<t}},z_t\right)$，或者简写为$h_{z_t}$，该表征与标准的Transformer是一致的。该内容表征同时编码了上下文和$x_{z_t}$本身。

• query representation(查询表征)$g_{\theta }(x_{z<t},z_t)$，简写为$g_{z_t}$。该表征仅仅接收上下文信息$x_{z<t}$和位置信息$z_t$，并不直接访问位置$z_t$对应的内容信息$x_{z_t}$。

从计算上来讲，第一层的query stream以一个可训练的向量来初始化，即$g_i^{(0)}=w$；content stream则是被初始化为word embedding，即$h_i^{(0)}=e(x_i)$。对每个自注意力层$m=1,...,M$，这两个stream表征按照以下的方式进行更新：

• Query stream：只能看到当前的位置信息，不能看到当前token的编码$x_{z_t}$
  $$g_{z_t}^{(m)}\leftarrow \text{ Attention }\left(\mathrm{Q}=g_{z_t}^{(m-1)},\mathrm{K}\mathrm{V}={\mathrm{h}}_{z_{<t}}^{(m-1)};\theta \right)$$

• Content stream(内容流自注意力)：传统self-attention，像GPT一样对当前token进行编码。同时可以看到位置$z_t$和编码内容$x_{z_t}$
  $$h_{z_t}^{(m)}\leftarrow \text{ Attention }\left(\mathrm{Q}=h_{z_t}^{(m-1)},\mathrm{K}\mathrm{V}={\mathrm{h}}_{z\le t}^{(m-1)};\theta \right)$$

其中的Q,K,V分别表示query,key和value。上述Content stream更新规则与标准的self-attention是相同的。预训练阶段最终预测只使用query stream，因为content stream已经见过当前token了。在微调阶段丢弃query steam，仅仅使用content stream(此时就是常规的Transformer-XL)，又回到了传统的self-attention结构。

Figure 2 的 a、b子图分别展示上述两种表征即Content表征$h_{z_t}$ 和 Query 表征$g_{z_t}$的学习。其中Content表征与Transformer的隐藏状态类似，它将同时编码输入本身的内容及上下文信息。Query 表征仅能获取上下文信息及当前的位置，它并不能获取当前位置的Content。

图 2:(a) 内容流注意力，与标准自注意力相同；(b)Query 流注意力，没有获取内容$x_{z_t}$ 的信息；©利用双流注意力的排列语言建模概览图。

部分预测：
虽然排列组合的自然语言目标有上述的优点，但是其排序组合所带来更具挑战的优化问题，实验收敛缓慢。因此本文提出了partial prediction进行简化，即只预测后面1/K个token，其中K是超参数。在形式上，将$z$分割成none-target子序列$z_{<=c}$和target子序列$z_{>c}$，其中$c$是切割点。其目标是最大化条件概率$log(p_{\theta }(x_{z>c}|x_{z<=c}))$，即在none-target子序列下target子序列的最大log似然函数：
$$\underset{\theta }{\max }{\mathbb{E}}_{\mathbf{z}\sim {\mathcal{Z}}_T}\left[\log p_{\theta }\left({\mathbf{x}}_{{\mathbf{z}}_{>c}}|{\mathbf{x}}_{{\mathbf{z}}_{\le c}}\right)\right]={\mathbb{E}}_{\mathbf{z}\sim {\mathcal{Z}}_T}\left[\sum _{t=c+1}^{|\mathbf{z}|}\log p_{\theta }\left(x_{z_t}|{\mathbf{x}}_{{\mathbf{z}}_{<t}}\right)\right]\text{\hspace{1em}(5)}$$
其中${\mathbf{z}}_{>}c$表示target，由于其在当前的排列组合$\mathbf{z}$的序列中拥有最长的上下文。用超参数$K$设置被预测的token个数为$1/K$，即$|\mathbf{z}|/(|\mathbf{z}|-c)\approx K$。对于没有被选中的额tokens，其query 表征就不需要计算了，同时节约了计算时间和内存空间。

2.4 Transformer-XL中的启发

到此，本文的目标函数可以和自回归框架相适应，那么本文进一步引入先进的自回归模型Transformer-XL（该工作也是作者此前的做出的）到预训练框架中。主要是为了学习到更长距离的信息。本文主要引入Transformer-XL中的2个技术：
(1)相对位置编码。这就是之前讨论的基于原始前向序列的。
(2)segment recurrence mechanism(段循环机制？？这样翻译吗？)。那么是如何将其引入排列组合模型，并使其能够复用历史片段的隐含状态。为了不失一般性，假设来自一个长序列$s$的两个segments：$x=s_{1:T}$，$x=s_{T+1:2T}$。让$z$和$z$分别表示$[1,...,T]$和$[T+1,...,2T]$的排列组合结果。基于$z$的排序组合，我们可以处理第一个segment，再对于每一层m，缓存所获得的content 表征$h^{(m)}$。对于下一个segment $x$，带有memory的attention可以通过以下进行更新：
$$h_{z_t}^{(m)}\leftarrow \text{ Attention }\left(\mathrm{Q}=h_{z_t}^{(m-1)},\mathrm{K}\mathrm{V}=\left[{\tilde{\mathbf{h}}}^{(m-1)},{\mathbf{h}}_{{\mathbf{z}}_{\le t}}^{(m-1)}\right];\theta \right)$$
其中$[..,..]$表示沿着序列方向的拼接。注意：位置编码仅仅依赖于原始序列中的真实位置。因此，上述的attention 更新，只要计算出$h^{(m)}$，则与$z$无关。这使得缓存并复用memory，而无需知晓先前segment的分解次序。我们所期望的是，该模型能够学习如何利用上一个segment的所有分解次序的memory。query stream也能够通过类似的方法计算得到。

2.5 Modeling Multiple Segments

上文一直阐述XLNet如何处理一个输入序列，但是下游任务可能存在多个输入segments，比如问答中的问题和上下文段落。这里主要讨论在自回归框架中如何预训练XLNet以处理多个segments的输入。与BERT类似，在预训练阶段，我们随机地采样2个segments(可以来自同一个content也可以不同)，并将2者拼接为一个序列，输入到排序组合语言模型中。我们只复用属于同一个上下文context的memory。排列组合模型的输入与BERT类似：[A，SEP，B，SEP，CLS]。其中SEP与CLS是人为预设的特殊字符，A和B表示2个segments。本文采用类似BERT的双segments的形式作为输入，那么XLNet是否也可以引入BERT中的下一句预测的优化目标呢？在BERT还有一个Next Sentence Prediction的优化目标，有助于finetune阶段直接适应各种类型的下游任务。XLNet也可以使用这种结构，只不过最后的消融研究结论是下一句预测任务对XLNet没什么帮助。

Relative Segment Encoding：
不同于BERT中采用的绝对segment编码方式，本文的XLNet提出了Relative Segment Encoding。BERT是在将每个位置的绝对segment编码加到word embedding中；A、B句，每个句子有个segment embedding。XLNet借鉴了Transformer-XL中的relative position的思想，并将其引入到segment encoding中。对于序列，给定其中的位置i和位置j，如果i和j来自于同一个segment，则使segment encoding $s_{ij}=s_{+}$，否则$s_{ij}=s_{-}$，其中$s_{+}和s_{-}$都是需要针对每个之前的attention训练而得到的参数。换一句说，只判断两个token是否在一个segment中，而不是判断他们各自属于哪个segment。当i需要注意到j时，则利用segment encoding $s_{ij}$计算attention 权重$a_{ij}={\left({\mathbf{q}}_i+\mathbf{b}\right)}^{\top }{\mathbf{s}}_{ij}$，其中$q_i$是标准attention操作中的query vector，$b$是待学习的head-specific bias vector。最后，将$a_{ij}$加到常规的attention 权重。简单说，是在计算attention weight的时候，给query额外操作一波，算出一个额外的权重加到原本的权重上去，跟relative positional encoding差不多。
这样做有2点好处，其一是相对位置的encoding能够提升归纳偏置的通用性；其二是为处理下游任务有多个输入segments的场景提供了解决方案，而这在使用绝对segment encoding是做不到的。BERT中的方案最多只能处理两个segments。

2.6 讨论和分析

2.6.1 与BERT的对比

对比方程（2）和方程（5）可以看出BERT和XLNet都进行部分预测，即仅仅预测序列中的部分子集，这也是为了降低优化难度。但是，。对于BERT来说，独立性假设使其不能够在targets之间的依存关系上建模。
以[New, York, is, a, city]为例来说，假设BERT和XLNet都选择2个token:[New, York]作为待预测的tokens， 并最大化$\log p(\text{ New York }|\text{ is a city })$。同时假设XLNet采样的分解次序是$[is,a,city,New,York]$，BERT和XLNet的目标分别如下：
$$\begin{array}{c}{\mathcal{J}}_{\mathrm{B}\mathrm{E}\mathrm{R}\mathrm{T}}=\log p(\mathrm{N}\mathrm{e}\mathrm{w}|\text{ is a city })+\log p(\text{ York }|\text{ is a city })\\ {\mathcal{J}}_{\text{ XLNet }}=\log p(\mathrm{N}\mathrm{e}\mathrm{w}|\text{ is a city })+\log p(\text{ York }|\mathrm{N}\mathrm{e}\mathrm{w},\text{ is a city })\end{array}$$
可以注意到XLNet是可以捕捉到$(New,York)$对之间的依赖关系，这在BERT中是被忽略的。 尽管BERT也是由学校部分依赖关系，如$(New,city)$和$(York，city)$， 但是显然在给定相同target和XLNet学得的依赖关系对更多,也就包含更多更密集的有效训练信息。

2.6.2 对比语言模型

标准的自回归语言模型如GPT只能够覆盖一部分依赖关系如(x=York,u=New)，其中u表示上下文；而无法覆盖到（x=New,u=York）；而XLNet是可以的，不仅可以，还可以覆盖到所有的排列组合。由此可见自回归模型的短板明显。比如问答任务中的上下文内容是“Thom Yorke is the singer of Radiohead”，问题是“Who is the singer of Radiohead”，对其进行span预测来作为答案。在自回归语言模型中“Thom Yorke”并不依赖于“Radiohead”，因此在标准语言模型中“Thom Yorke”并不会被选为答案。标准的语言模型一般是使用将所有token的representations输入到softmax中。

ELMo则是简单将前向和反向的语言模型拼接，这仅仅浅层的特征拼接，缺乏双向的深度互动建模。
XLNet与其他语言模型的对比结果如下：

3.实验结果

结果确实提升很大，具体参考原文，这里就不细说了。

4.结论

XLNet提出了一个通用的自回归预训练方法，该方法综合了自回归方法和自编码器方法提出了一种排列组合语言模型目标。XLNet的网络框架可以无缝地在自回归目标上工作，包括集成的Transformer-XL和双流注意力机制。XLNet在多个task上取得了实质性进展，并刷新多项记录。

5.附录：基于双向流自注意力的Target-Aware Representation

5.1 标准语言模型参数化为何会失败的实例

举例说明在排列组合目标下，标准语言模型参数化为何会失败。假设有2个排列组合${\mathbf{z}}^{(1)}$和${\mathbf{z}}^{(2)}$，二者满足以下关系：
$${\mathbf{z}}_{<t}^{(1)}={\mathbf{z}}_{<t}^{(2)}={\mathbf{z}}_{<t}\text{ but }{z}_t^{(1)}=i̸=j=z_t^{(2)}$$
可以看出，在$t$位置之前的子序列是相同的，但是在$i$和$j$位置不同。
用这2种组合分别替代原始的参数。可以得到：
$$\underset{z_t^{(1)}=i,{\mathbf{z}}_{<t}^{(1)}={\mathbf{z}}_{<t}}{p_{\theta }\left(X_i=x|{\mathbf{x}}_{{\mathbf{z}}_{<}t}\right)}=\underset{{\mathbf{z}}_t^{(1)}=j,{\mathbf{z}}_{<t}^{(2)}={\mathbf{z}}_{<t}}{p_{\theta }\left(X_j=x|{\mathbf{x}}_{{\mathbf{z}}_{<t}}\right)}=\frac{\exp \left(e(x{)}^{\top }h\left({\mathbf{x}}_{{\mathbf{z}}_{<t}}\right)\right)}{{\sum }_{x^{\prime }}\exp \left(e{\left(x^{\prime }\right)}^{\top }h\left({\mathbf{x}}_{{\mathbf{z}}_{<t}}\right)\right)}$$
实际上，不同的target位置$i$和$j$完全共享共享的预测，但是这2个位置的真实分布应该是不同的。

5.2 双流注意力

这里提供Transformer-XL中双流注意力的细节。初始化representation：
$$\forall t=1,\dots ,T:h_t=e\left(x_t\right)\text{ and }{g}_t=w$$
从历史segment缓存得到第m层 content representation(memory)：$\tilde{\mathbf{h}}(m)$。
对于Transformer-XL中的每一层$m=1,..,M$，相对位置的encoding和position-wise feed-forward相继用以更新representations：
$\forall t=1,\dots ,T:$
$$\begin{array}{l}{\hat{h}}_{z_t}^{(m)}=\text{ LayerNorm }\left(h_{z_t}^{(m-1)}+\mathrm{RelAtn}\left(h_{z_t}^{(m-1)},\left[{\tilde{\mathbf{h}}}^{(m-1)},{\mathbf{h}}_{\mathbf{z}\le t}^{(m-1)}\right]\right)\right)\\ h_{z_t}^{(m)}=\text{ LayerNorm }\left({\hat{h}}_{z_t}^{(m)}+\mathrm{PosFF}\left({\hat{h}}_{z_t}^{(m)}\right)\right)\\ {\hat{g}}_{z_t}^{(m)}=\text{ LayerNorm }\left(g_{z_t}^{(m-1)}+\mathrm{RelAtn}\left(g_{z_t}^{(m-1)},\left[{\tilde{\mathbf{h}}}^{(m-1)},{\mathbf{h}}_{z_{\le t}}^{(m-1)}\right]\right)\right)\\ g_{z_t}^{(m)}=\text{ LayerNorm }\left({\hat{g}}_{z_t}^{(m)}+\mathrm{PosFF}\left({\hat{g}}_{z_t}^{(m)}\right)\right)\end{array}$$
Target-aware预测分布：
$$p_{\theta }\left(X_{z_t}=x|{\mathbf{x}}_{z_{<t}}\right)=\frac{\exp \left(e(x{)}^{\top }{g}_{z_t}^{(M)}\right)}{{\sum }_{x^{\prime }}\exp \left(e{\left(x^{\prime }\right)}^{\top }{g}_{z_t}^{(M)}\right)}$$

5.3 超参数

略

5.4 memory和排列组合的图文说明

这里以图文形式进一步介绍排列组合语言模型的建模目标，包括memory复用机制(即，recurrence mechanism)、如何在排列组合的分解序列中使用attention masks以及两种attention streams。具体如Figure3和4所示：
对于给定当前位置$z_t$；其attention mask是由其排列组合结果$\mathbf{z}$决定的，attention mask是用以决定只有在$z_t$之前组合序列才会被attented到，即$z_i，i<t$。这也是自回归语言模型的操作。对比Figure 3和4，可以看到在给定一个排列组合后，利用attention masks，query stream和 content stream的不同工作过程。主要的不同在于：query stream不能够进行self-attention，也不能够看自己的位置的编码内容，而仅仅有位置信息；但是content stream却是多可以，即content stream是正常的self-attention。
下面2图，可以好好详细地多看几遍：
Content stream：

Query stream：