卡尔曼滤波及其在配对交易中的应用--Python落地
感谢周航和郭增岳的投稿,人工智能与量化交易公众号的运营者,他们热衷于人工智能和量化投资方面的研究。
前言
听过卡尔曼滤波的差不多有两年的时间了,虽然大致上明白其原理,但是也是直到现在才能够彻底掌握下来。主要是卡尔曼滤波算法涉及到比较复杂的数学公式推导。在很多博客上都有写卡尔曼滤波的相关文章,但都是花非常大的篇幅来通过一些例子来通俗地讲解卡尔曼滤波,对于不知道其数学原理的读者来说,看完之后依然是一知半解。
本文会先讲解最简单的单变量卡尔曼滤波,让大家知道卡尔曼滤波大致是什么样的,然后再详细地给出公式的推导过程,最后展示卡尔曼滤波在配对交易中的应用。
卡尔曼滤波
卡尔曼滤波(Kalman filtering)一种利用线性系统状态方程,通过系统输入输出观测数据,对系统状态进行最优估计的算法。由于观测数据中包括系统中的噪声和干扰的影响,所以最优估计也可看作是滤波过程。
最简单的单变量卡尔曼滤波,可以认为,我们观测的时间序列是存在噪声的,而我们可以通过卡尔曼滤波,过滤掉噪声,而得到了去除噪声之后的状态序列















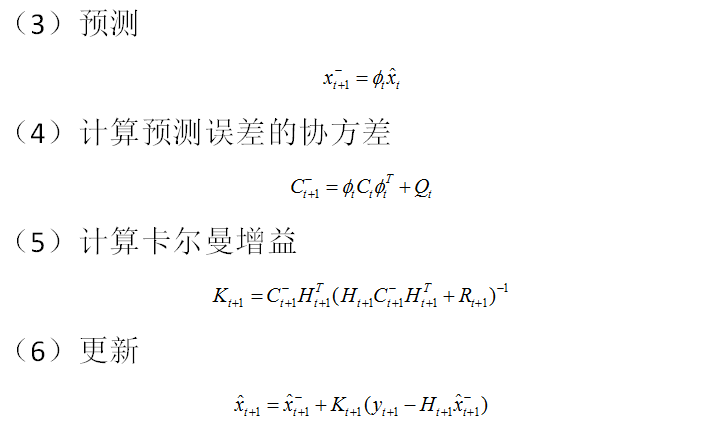
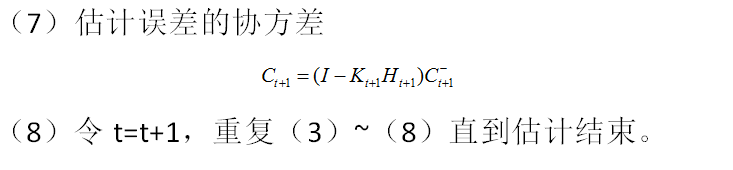
卡尔曼滤波在配对交易中的应用
关于什么配对交易,什么是统计套利中的协整,知乎上有非常好的回答,在这里我们只讨论卡尔曼滤波在配对交易中的应用。
在配对交易中,我们构造了如下回归方程
然后利用该方程在样本外进行套利。那么,假如我们这里的a和B是会改变的,那么我们如何动态地去调整回归方程的系数?我们可以使用如下滤波的方式
建立观测方程
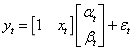
建立状态方程
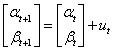
我们需要估计的状态为
下面以焦炭和螺纹为例,采用焦炭和螺纹主力连续合约的收盘价数据


# 以焦炭的收盘价数据作为x,螺纹的收盘价数据作为y# 螺纹价格 = alpha + beta * 焦炭价格 + 随机误差 from pykalman import KalmanFilter#建立观测矩阵observation_matrices = np.vstack(( np.ones(len(df[:'2013'])), df.loc[:'2013','焦炭'].values )).TShape = observation_matrices.shapeobservation_matrices = observation_matrices.reshape(Shape[0],1,Shape[1])#定义卡尔曼滤波的方程kf = KalmanFilter(transition_matrices=np.array([[1,0],[0,1]]), #转移矩阵为单位阵 observation_matrices=observation_matrices)np.random.seed(0)# 使用2013年以前的数据,采用EM算法,估计出初始状态,# 初始状态的协方差,观测方程和状态方程误差的协方差kf.em(df.loc[:'2013','螺纹'])#对2013年的数据做滤波filter_mean,filter_cov = kf.filter(df.loc[:'2013','螺纹'])#观测值为螺纹#从2014年开始滚动start_index = np.where(df.index.year==2014)[0][0]for i in range(start_index,len(df)): observation_matrix = np.array([[1,df['焦炭'].values[i]]]) observation = df['螺纹'].values[i] #以上一个时刻的状态,状态的协方差以及当前的观测值,得到当前状态的估计 next_filter_mean,next_filter_cov = kf.filter_update( filtered_state_mean = filter_mean[-1], filtered_state_covariance = filter_cov[-1], observation = observation, observation_matrix = observation_matrix) filter_mean = np.vstack((filter_mean,next_filter_mean)) filter_cov = np.vstack((filter_cov,next_filter_cov.reshape(1,2,2)))#得到alpha和betaalpha = pd.Series(filter_mean[start_index:,0], index = df.index[start_index:])beta = pd.Series(filter_mean[start_index:,1], index = df.index[start_index:])
# 螺纹价格 = alpha + beta * 焦炭价格 + 随机误差
from pykalman import KalmanFilter
#建立观测矩阵
observation_matrices = np.vstack(( np.ones(len(df[:'2013'])),
df.loc[:'2013','焦炭'].values )).T
Shape = observation_matrices.shape
observation_matrices = observation_matrices.reshape(Shape[0],1,Shape[1])
#定义卡尔曼滤波的方程
kf = KalmanFilter(transition_matrices=np.array([[1,0],[0,1]]), #转移矩阵为单位阵
observation_matrices=observation_matrices)
np.random.seed(0)
# 使用2013年以前的数据,采用EM算法,估计出初始状态,
# 初始状态的协方差,观测方程和状态方程误差的协方差
kf.em(df.loc[:'2013','螺纹'])
#对2013年的数据做滤波
filter_mean,filter_cov = kf.filter(df.loc[:'2013','螺纹'])#观测值为螺纹
#从2014年开始滚动
start_index = np.where(df.index.year==2014)[0][0]
for i in range(start_index,len(df)):
observation_matrix = np.array([[1,df['焦炭'].values[i]]])
observation = df['螺纹'].values[i]
#以上一个时刻的状态,状态的协方差以及当前的观测值,得到当前状态的估计
next_filter_mean,next_filter_cov = kf.filter_update(
filtered_state_mean = filter_mean[-1],
filtered_state_covariance = filter_cov[-1],
observation = observation,
observation_matrix = observation_matrix)
filter_mean = np.vstack((filter_mean,next_filter_mean))
filter_cov = np.vstack((filter_cov,next_filter_cov.reshape(1,2,2)))
#得到alpha和beta
alpha = pd.Series(filter_mean[start_index:,0], index = df.index[start_index:])
beta = pd.Series(filter_mean[start_index:,1], index = df.index[start_index:])

There is always someone to learn from
在学习的路上
你永远不会独行