python机器学习库sklearn——DBSCAN密度聚类
全栈工程师开发手册 (作者:栾鹏)
python数据挖掘系列教程
DBSCAN密度聚类的相关的知识内容可以参考
http://blog.csdn.net/luanpeng825485697/article/details/79438025
DBSCAN
The DBSCAN 算法将聚类视为被低密度区域分隔的高密度区域。由于这个相当普遍的观点, DBSCAN发现的聚类可以是任何形状的,与假设聚类是 convex shaped 的 K-means 相反。 DBSCAN 的核心概念是 core samples, 是指位于高密度区域的样本。 因此一个聚类是一组核心样本,每个核心样本彼此靠近(通过一定距离度量测量) 和一组接近核心样本的非核心样本(但本身不是核心样本)。算法中的两个参数, min_samples 和 eps,正式的定义了我们所说的 dense(稠密)。较高的 min_samples 或者较低的 eps表示形成聚类所需的较高密度。
更正式的,我们定义核心样本是指数据集中的一个样本,存在 min_samples 个其他样本在 eps 距离范围内,这些样本被定为为核心样本的邻居 neighbors 。这告诉我们核心样本在向量空间稠密的区域。 一个聚类是一个核心样本的集合,可以通过递归来构建,选取一个核心样本,查找它所有的 neighbors (邻居样本) 中的核心样本,然后查找 their (新获取的核心样本)的 neighbors (邻居样本)中的核心样本,递归这个过程。 聚类中还具有一组非核心样本,它们是集群中核心样本的邻居的样本,但本身并不是核心样本。 显然,这些样本位于聚类的边缘。
根据定义,任何核心样本都是聚类的一部分,任何不是核心样本并且和任意一个核心样本距离都大于eps 的样本将被视为异常值。
DBSCAN密度聚类过程:
1、构造数据集。
2、使用数据集进行DBSCAN密度聚类算法。
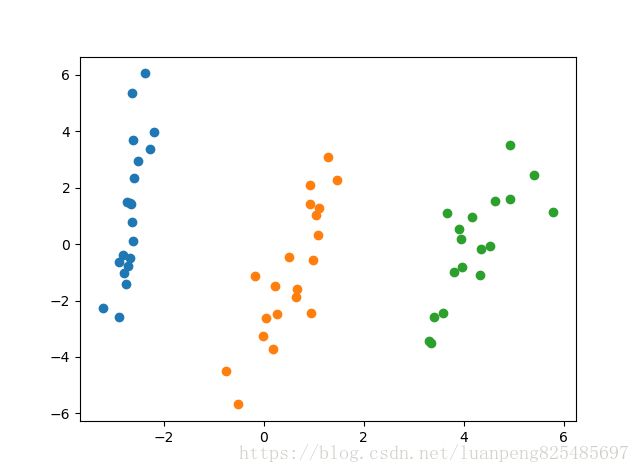
3、可视化聚类效果。
import numpy as np # 数据结构
import sklearn.cluster as skc # 密度聚类
from sklearn import metrics # 评估模型
import matplotlib.pyplot as plt # 可视化绘图
data=[
[-2.68420713,1.469732895],[-2.71539062,-0.763005825],[-2.88981954,-0.618055245],[-2.7464372,-1.40005944],[-2.72859298,1.50266052],
[-2.27989736,3.365022195],[-2.82089068,-0.369470295],[-2.62648199,0.766824075],[-2.88795857,-2.568591135],[-2.67384469,-0.48011265],
[-2.50652679,2.933707545],[-2.61314272,0.096842835],[-2.78743398,-1.024830855],[-3.22520045,-2.264759595],[-2.64354322,5.33787705],
[-2.38386932,6.05139453],[-2.6225262,3.681403515],[-2.64832273,1.436115015],[-2.19907796,3.956598405],[-2.58734619,2.34213138],
[1.28479459,3.084476355],[0.93241075,1.436391405],[1.46406132,2.268854235],[0.18096721,-3.71521773],[1.08713449,0.339256755],
[0.64043675,-1.87795566],[1.09522371,1.277510445],[-0.75146714,-4.504983795],[1.04329778,1.030306095],[-0.01019007,-3.242586915],
[-0.5110862,-5.681213775],[0.51109806,-0.460278495],[0.26233576,-2.46551985],[0.98404455,-0.55962189],[-0.174864,-1.133170065],
[0.92757294,2.107062945],[0.65959279,-1.583893305],[0.23454059,-1.493648235],[0.94236171,-2.43820017],[0.0432464,-2.616702525],
[4.53172698,-0.05329008],[3.41407223,-2.58716277],[4.61648461,1.538708805],[3.97081495,-0.815065605],[4.34975798,-0.188471475],
[5.39687992,2.462256225],[2.51938325,-5.361082605],[4.9320051,1.585696545],[4.31967279,-1.104966765],[4.91813423,3.511712835],
[3.66193495,1.0891728],[3.80234045,-0.972695745],[4.16537886,0.96876126],[3.34459422,-3.493869435],[3.5852673,-2.426881725],
[3.90474358,0.534685455],[3.94924878,0.18328617],[5.48876538,5.27195043],[5.79468686,1.139695065],[3.29832982,-3.42456273]
]
X = np.array(data)
db = skc.DBSCAN(eps=1.5, min_samples=3).fit(X) #DBSCAN聚类方法 还有参数,matric = ""距离计算方法
labels = db.labels_ #和X同一个维度,labels对应索引序号的值 为她所在簇的序号。若簇编号为-1,表示为噪声
print('每个样本的簇标号:')
print(labels)
raito = len(labels[labels[:] == -1]) / len(labels) #计算噪声点个数占总数的比例
print('噪声比:', format(raito, '.2%'))
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0) # 获取分簇的数目
print('分簇的数目: %d' % n_clusters_)
print("轮廓系数: %0.3f" % metrics.silhouette_score(X, labels)) #轮廓系数评价聚类的好坏
for i in range(n_clusters_):
print('簇 ', i, '的所有样本:')
one_cluster = X[labels == i]
print(one_cluster)
plt.plot(one_cluster[:,0],one_cluster[:,1],'o')
plt.show()再来一个案例
import numpy as np
from sklearn.cluster import DBSCAN
from sklearn import metrics
from sklearn.datasets.samples_generator import make_blobs
from sklearn.preprocessing import StandardScaler
# #############################################################################
# 产生样本数据
centers = [[1, 1], [-1, -1], [1, -1]] # 生成聚类中心点
X, labels_true = make_blobs(n_samples=750, centers=centers, cluster_std=0.4,random_state=0) # 生成样本数据集
X = StandardScaler().fit_transform(X) # StandardScaler作用:去均值和方差归一化。且是针对每一个特征维度来做的,而不是针对样本。
# #############################################################################
# 调用密度聚类 DBSCAN
db = DBSCAN(eps=0.3, min_samples=10).fit(X)
# print(db.labels_) # db.labels_为所有样本的聚类索引,没有聚类索引为-1
# print(db.core_sample_indices_) # 所有核心样本的索引
core_samples_mask = np.zeros_like(db.labels_, dtype=bool) # 设置一个样本个数长度的全false向量
core_samples_mask[db.core_sample_indices_] = True #将核心样本部分设置为true
labels = db.labels_
# 获取聚类个数。(聚类结果中-1表示没有聚类为离散点)
n_clusters_ = len(set(labels)) - (1 if -1 in labels else 0)
# 模型评估
print('估计的聚类个数为: %d' % n_clusters_)
print("同质性: %0.3f" % metrics.homogeneity_score(labels_true, labels)) # 每个群集只包含单个类的成员。
print("完整性: %0.3f" % metrics.completeness_score(labels_true, labels)) # 给定类的所有成员都分配给同一个群集。
print("V-measure: %0.3f" % metrics.v_measure_score(labels_true, labels)) # 同质性和完整性的调和平均
print("调整兰德指数: %0.3f" % metrics.adjusted_rand_score(labels_true, labels))
print("调整互信息: %0.3f" % metrics.adjusted_mutual_info_score(labels_true, labels))
print("轮廓系数: %0.3f" % metrics.silhouette_score(X, labels))
# #############################################################################
# Plot result
import matplotlib.pyplot as plt
# 使用黑色标注离散点
unique_labels = set(labels)
colors = [plt.cm.Spectral(each) for each in np.linspace(0, 1, len(unique_labels))]
for k, col in zip(unique_labels, colors):
if k == -1: # 聚类结果为-1的样本为离散点
# 使用黑色绘制离散点
col = [0, 0, 0, 1]
class_member_mask = (labels == k) # 将所有属于该聚类的样本位置置为true
xy = X[class_member_mask & core_samples_mask] # 将所有属于该类的核心样本取出,使用大图标绘制
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),markeredgecolor='k', markersize=14)
xy = X[class_member_mask & ~core_samples_mask] # 将所有属于该类的非核心样本取出,使用小图标绘制
plt.plot(xy[:, 0], xy[:, 1], 'o', markerfacecolor=tuple(col),markeredgecolor='k', markersize=6)
plt.title('Estimated number of clusters: %d' % n_clusters_)
plt.show()