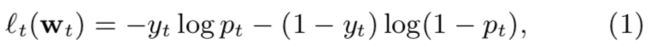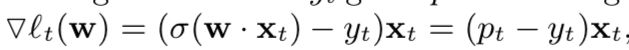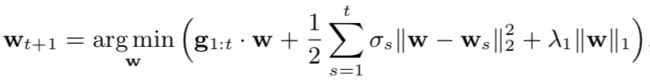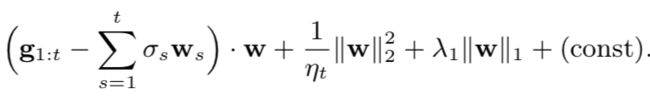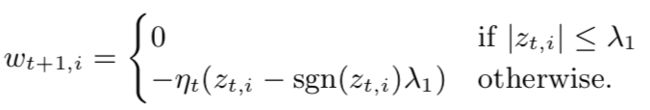FTRL-Proximal
Ad Click Prediction: a View from the Trenches
ABSTRACT
广告点击率预测是一个大规模的学习问题,对数十亿美元的在线广告行业至关重要。我们从部署的CTR预测系统的设置中提供了一些案例研究和从最近的实验中提取的话题,包括基于FTRL-Proximal在线学习算法(具有出色的稀疏性和收敛特性)以及使用每个坐标学习率的传统监督学习语境的改进。
我们也探讨了现实世界系统中出现的一些挑战,它们最初可能出现在传统机器学习研究领域之外,包括用于节省内存的有效技巧,用于评估和可视化性能的方法,用于提供预测概率的置信度估计的实用方法,校准方法以及自动管理特征的方法。最后,我们还详细介绍了几个对我们没有效果的方向,尽管文献中的其他方面都有其成果。本文目的是突出现在的工业环境中理论进展与实际工程之间的密切关系,并展示在复杂动态系统中应用传统机器学习方法时出现的挑战深度。
KEYWORDS
在线广告,数据挖掘,大规模学习
1、INTRODUCTION
在线广告是一个价值数十亿美元的行业,已成为机器学习的重要成功案例之一。赞助搜索广告,内容相关广告,展示广告和实时出价拍卖都严重依赖于学习模型准确,快速,可靠地预测广告点击率的能力。这个问题的设定也促使该领域解决了甚至十年前几乎不可想象的规模问题。典型的工业模型可以使用相应大小的特征空间提供每天数十亿事件的预测,然后从所得到的大量数据中学习。
在本文中,我们提供了一系列案例研究,这些案例研究来自最近的实验,用于设置Google使用的部署系统,以预测赞助搜索广告的广告点击率。由于此问题设置现已得到充分研究,因此我们选择关注一系列受到较少关注但在工作系统中同样重要的主题。因此,我们探讨了内存节省,性能分析,预测置信度,校准和特征管理等问题,这些问题与传统上设计有效学习算法的问题相同。本文的目的是让读者了解真实工业环境中出现的挑战深度,以及分享可能应用于其他大规模问题领域的技巧和见解。
2、BRIEF SYSTEM OVERVIEW
当用户进行搜索q时,基于广告商选择的关键字将初始候选广告集与查询q匹配。然后,拍卖机制确定是否向用户显示这些广告,他们显示的顺序以及广告商在点击广告时支付的价格。除了广告客户出价之外,对于每个广告a,拍卖的重要输入是P的估计(click| q,a),即该广告如果显示将被点击的概率。
我们系统中使用的特征来自各种来源,包括查询,广告创意文本和各种与广告相关的元数据。数据往往非常稀疏,每个示例通常只有很小一部分非零特征值。
正则化逻辑回归等方法非常适合此问题设置,每天需要进行数十亿次预测,并在观察到新点击和非点击时快速更新模型。当然,这个数据速率意味着训练数据集巨大,数据由基于Photon系统的流媒体服务提供并进行全面讨论。
由于近年来大规模学习已经得到了很好的研究,我们在本文中并未投入大量篇幅来详细描述我们的系统架构。然而我们注意到,训练方法与Google Brain团队描述的倾斜SGD方法相似,不同之处在于我们训练的是单层模型而不是多层的深层网络。这使我们能够处理比我们所知的更大数据集与模型,有数十亿个系数。由于训练好的模型被复制到许多数据中心进行服务,我们更关心的是在服务时而不是在训练期间进行稀疏化。
3、ONLINE LEARNING AND SPARSITY
对于大规模学习,用于广义线性模型的在线算法(例如逻辑回归)有许多优点,尽管特征向量x可能有多个维度,但通常每个实例只有几百个非零值,这可以通过磁盘或网络上的流式传输实现对大型数据集的高效训练,因为每个样本只需要被使用一次。
为准确描述算法,我们需要先定义一些符号。gt ∈ Rd中t表示当前训练实例的索引,gt,i表示向量gt的第i个输入,同时有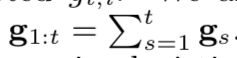 。
。
如果我们想要使用逻辑回归对问题建模,可以使用以下线上框架。在第t轮,我们要求使用特征为xt ∈ Rd的训练样本预测,给定参数wt,则预测值pt=σ(wt · xt),其中σ(a) = 1/(1 + exp(−a))是sigmoid函数。然后我们观察标签值yt ∈ {0, 1},得到损失函数
梯度用于优化
在线梯度下降(OGD)已证明对这类问题非常有效,以最少的计算资源准确的预测,然而实际需要考虑的另一个关键因素是最终模型的大小。由于模型可以稀疏存储,因此w中非零系数的数量是内存使用的决定因素。 不幸的是,OGD在稀疏模型方面效果一般。实际上,简单的对损失函数加上L1惩罚项的次梯度不会产生0值的参数。更复杂的如FOBOS和truncated gradient(截断的梯度,直接截断方法是每隔k次就不更新参数)等方法确实成功引入了稀疏性。与FOBOS相比,正则化双平均(RDA)算法以一定的稀疏性为代价得到更高的准确度[32]。然而,我们观察到梯度下降方法在我们的数据集上比RDA准确度更高,我们使用“Follow The (Proximally) Regularized Leader”算法(FTRL-Proximal)同时获得RDA提供的稀疏性和OGD的准确度。如果没有正则化,该算法与标准在线梯度下降算法等价,但由于它使用模型系数w的可选惰性表示,因此可以更有效地实现L1正则化。
给定一系列梯度gt∈Rd,OGD的参数更新如下:wt+1 = wt − ηtgt,其中ηt是非递增学习率,比如。
而FTRL-Proximal算法更新参数如下:
其中σs是学习率,因此σ1:t = 1/ηt。
λ1 = 0时,2个更新方式的等价;λ1 > 0时,FTRL-Proximal产生稀疏模型。
从公式来看,有人可能会觉得实现FTRL比实现OGD更难或者需要存储过去的所有参数,但实际上在整个过程中只需要存储一份参数,我们可以将argmin函数重写为
因此,如果我们已经存了![]() ,那么在第t轮更新的开始我们只要zt = zt-1+gt+
,那么在第t轮更新的开始我们只要zt = zt-1+gt+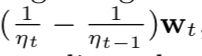 ,然后用闭包形式求得wt+1
,然后用闭包形式求得wt+1
FTRL-Proximal把z存起来,而OGD存的是w。Algorithm1是伪代码,还加入了per-coordinate学习率规划项并且加入了支持L2正则的参数λ2。我们也能直接存储−ηtzt而不是zt,此时当λ1 = 0时我们存的就是在线梯度参数,当ηt是一个常量并且λ1 = 0时,公式就等价于在线梯度下降,因为 。
。
实验结果
在小数据集上带有L1正则项的FTRL-Proximal在模型大小和精确度的tradeoff上明显优于RDA和FOBOS,见table1的第2、3行。在许多情况下,简单的启发式方法几乎与更多规则的方法一样,但这不是其中之一。我们的稻草人算法,OGD-Count仅仅保留了它看到一个特征的次数,直到该次数超过阈值k,系数固定为0,但是在计数k次之后,在线梯度下降(不带L1正则项)照常进行。为了测试FTRL-Proximal对这个更简单的启发式算法,我们实验了一个非常大的数据集。我们调整k以产生与FTRL-Proximal相同的精确度,使用更大的k导致更差的AucLoss,结果在table1第4行。 总的来说,这些结果表明FTRL-Proximal具有明显改善的稀疏性,具有相同或更好的预测准确性。
3.1 Per-Coordinate Learning Rates
在线梯度下降的标准理论建议使用全局学习率ηt=1/√t,对于所有坐标都相同,但是可能效果并不理想:假设我们使用逻辑回归估计10个硬币的Pr(heads | coini),每一轮t,单个硬币i被翻转,我们看到特征向量x∈R10,其中Xi = 1且xj =0,j ≠i,因此我们基本上将10个独立的逻辑回归问题打包成一个问题。 我们可以运行10个独立的在线梯度下降,其中问题i使用的学习率是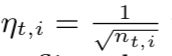 ,其中nt,i是硬币i至今被翻转的次数。如果硬币i比硬币j更频繁地翻转,那么硬币i的学习率将更快地下降,反映出我们有更多数据的事实,而硬币j的学习率将保持较高,因为我们对当前估计的置信度不足,因此需要对新数据做出更快的反应。
,其中nt,i是硬币i至今被翻转的次数。如果硬币i比硬币j更频繁地翻转,那么硬币i的学习率将更快地下降,反映出我们有更多数据的事实,而硬币j的学习率将保持较高,因为我们对当前估计的置信度不足,因此需要对新数据做出更快的反应。
另一方面,如果我们将其看成一个单独的学习问题,标准学习率框架下ηt=1/√t会应用在每个坐标维度,此时即使硬币i没有被翻转,我们的学习率也下降了,显然不行。事实上有人证明了标准算法的性能渐渐比分成独立问题差得多,因此至少对于某些问题,每个坐标不同的学习率可以提供实质性的优势。假设gs,i 是梯度gs =▽ls(ws)的第i个坐标,以下公式使结果接近最优。
在实验中,我们使用α和β以在渐进验证中性能最好的学习率,还尝试在nt,i上使用指数,而不是0.5。 α的最佳值可以根据特征和数据集而变化,β= 1通常够好,这可以保证刚开始的学习率不会太高。如上所述,该算法要求我们跟踪每个特征的梯度之和和梯度的平方和,4.5节介绍了一种节约内存的公式,其中梯度的平方和在许多模型上摊销。
实验结果
我们通过测试两个相同的模型来评估单坐标学习率的影响,一个使用全局学习率,一个使用单坐标学习率。基本参数α针对每个模型单独调整。我们使用了代表性数据集,并使用AucLoss作为评估指标(参见第5节)。结果显示,与全球学习率基线相比,使用每坐标学习率可将AucLoss降低11.2%。为了将这个结果放在上下文中,在我们的设置中,AucLoss减少1%被认为是大的。