八大排序算法java代码、复杂度比较以及应用场景

目录

 

八大排序算法

冒泡排序

插入排序

归并排序

快速排序

基数排序

选择排序

希尔排序

算法比较

应用场景

---

八大排序算法

所谓排序，就是使一串记录，按照其中的某个或某些关键字的大小，递增或递减的排列起来的操作。

冒泡排序

基本思想：（图片转自这里）

1. 比较相邻的元素。如果第一个比第二个大，就交换他们两个。
2. 对每一对相邻元素做同样的工作，从开始第一对到结尾的最后一对。在这一点，最后的元素应该会是最大的数。
3. 针对所有的元素重复以上的步骤，除了最后一个。
4. 持续每次对越来越少的元素重复上面的步骤，直到没有任何一对数字需要比较。

代码如下：

package com.sort;
public class BubbleSort {
	public static void bubblesort(int[] arr) {
		int temp = 0;
		for (int i = 0; i < arr.length; i++) {
			for (int j = 0; j < arr.length - i - 1; j++) {
				if (arr[j] > arr[j + 1]) {
					temp = arr[j + 1];
					arr[j + 1] = arr[j];
					arr[j] = temp;
				}
			}
		}
	}
	public static void main(String[] args) {
		int[] arr = { 10, 5, 8, 9, 4, 3, 1, 6, 7, 2 };
		bubblesort(arr);
		for (int k = 0; k < arr.length; k++)
			System.out.print(arr[k] + " ");
	}
}

堆排序

基本思想：利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆积的性质：即子结点的键值或索引总是小于（或者大于）它的父节点。（图片转自这里）

代码如下：

package com.sort;

public class HeapSort {
	public static void heapAdjust(int[] arr, int s, int m) {
		int temp, i, largest;// largest中存关键字较大的记录下标
		temp = arr[s - 1];
		for (i = 2 * s; i < m; i = i * 2) {
			if (arr[i - 1] < arr[i]) {
				largest = i;
				i++;
			} else {
				largest = i - 1;
			}
			if (temp >= arr[largest])
				break;
			arr[s - 1] = arr[largest];
			s = largest + 1;
		}
		arr[s - 1] = temp;
	}
	public static void swap(int[] array, int from, int to) {
		int temp;
		temp = array[from];
		array[from] = array[to];
		array[to] = temp;
	}
	public static void heapsort(int[] arr) {
		for (int i = arr.length / 2; i > 0; i--) {
			heapAdjust(arr, i, arr.length);
		}
		for (int j = arr.length - 1; j > 0; j--) {
			swap(arr, 0, j);
			heapAdjust(arr, 1, j);
		}
	}
	public static void main(String[] args) {
		int[] arr = { 5, 10, 8, 9, 4, 3, 1, 6, 7, 2 };
		heapsort(arr);
		for (int k = 0; k < arr.length; k++)
			System.out.print(arr[k] + " ");
	}
}

插入排序

基本思想：每步将一个待排序的记录，按其关键码值的大小插入前面已经排序的文件中适当位置上，直到全部插入完为止。类似于打扑克牌的抓牌。（图片转自这里）

代码如下：

package com.sort;

public class InsertSort {
	public static void insertSort(int[] arr) {
		int temp = 0;
		int i, j;
		for (i = 1; i < arr.length; i++) {
			if (arr[i] < arr[i - 1]) {
				temp = arr[i];
				for (j = i; j > 0 && temp < arr[j - 1]; j--) {
					arr[j] = arr[j - 1];
				}
				arr[j] = temp;
			}
		}

	}
	public static void main(String[] args) {
		int[] arr = { 10, 5, 8, 9, 4, 3, 1, 6, 7, 2 };
		insertSort(arr);
		for (int k = 0; k < arr.length; k++)
			System.out.print(arr[k] + " ");
	}
}

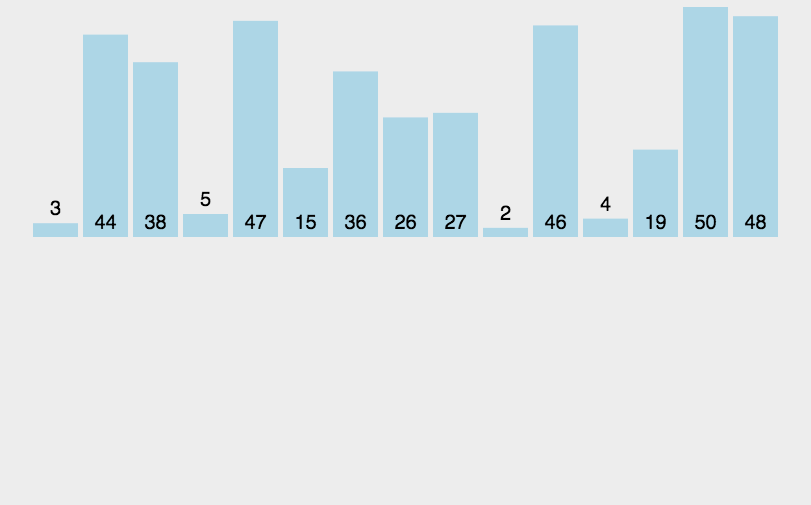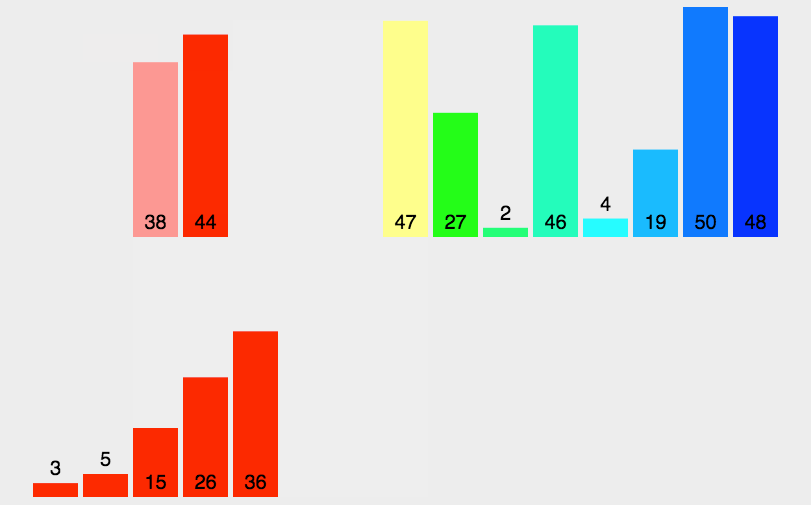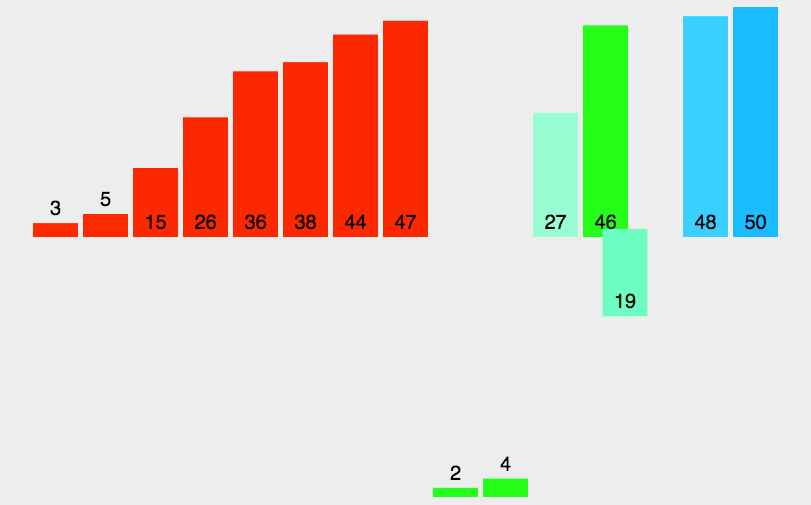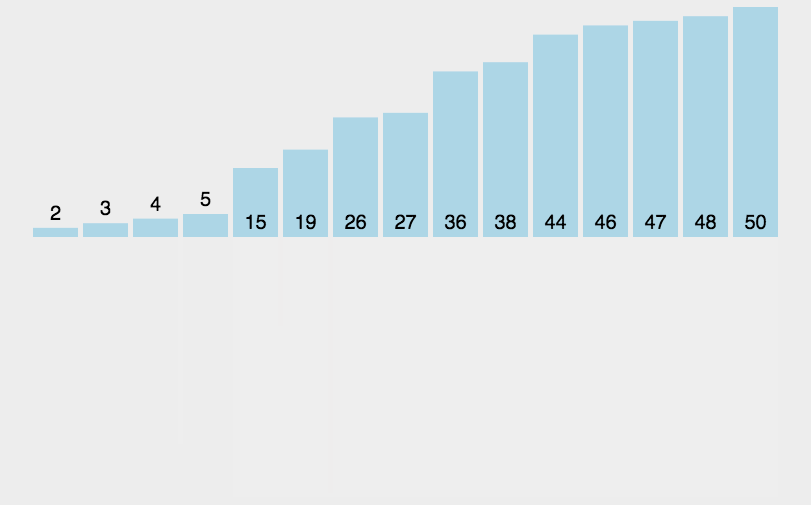
归并排序

基本思想（图片转自这里）

• 第一步：申请空间，使其大小为两个已经排序序列之和，该空间用来存放合并后的序列
• 第二步：设定两个指针，最初位置分别为两个已经排序序列的起始位置
• 第三步：比较两个指针所指向的元素，选择相对小的元素放入到合并空间，并移动指针到下一位置
• 重复步骤3直到某一指针超出序列尾，然后将另一序列剩下的所有元素直接复制到合并序列尾

代码如下：

package com.sort;
public class MergeSort {
	public static void merge(int[] arr, int start, int mid, int end) {
		int[] temp = new int[arr.length];
		int i = start, j = mid + 1, k = start;
		while (i <= mid && j <= end) {
			if (arr[i] <= arr[j])
				temp[k++] = arr[i++];
			else
				temp[k++] = arr[j++];
		}
		while (i <= mid)
			temp[k++] = arr[i++];
		while (j <= end)
			temp[k++] = arr[j++];
		for (int l = start; l <= end; l++)
			arr[l] = temp[l];
	}

	public static void mergesort(int[] arr, int start, int end) {
		if (start < end) {
			int mid = (start + end) / 2;
			mergesort(arr, start, mid);
			mergesort(arr, mid + 1, end);
			merge(arr, start, mid, end);
		}
	}

	public static void main(String[] args) {
		int[] arr = { 5, 10, 8, 9, 4, 3, 1, 6, 7, 2 };
		mergesort(arr, 0, arr.length - 1);
		for (int k = 0; k < arr.length; k++)
			System.out.print(arr[k] + " ");
	}
}

快速排序

基本思想：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。（图片转自这里）

代码如下：

package com.sort;

public class QuickSort {
	public static void quicksort(int[] arr, int start, int end) {
		if (start < end) {
			int index = partition(arr, start, end);
			quicksort(arr, start, index - 1);
			quicksort(arr, index + 1, end);
		}
	}

	private static int partition(int[] arr, int start, int end) {
		int flag = arr[start];
		int i = start, j = end;
		while (i < j) {
			while (i < j && arr[j] >= flag)
				j--;
			if (i < j)
				arr[i++] = arr[j];
			while (i < j && arr[i] <= flag)
				i++;
			if (i < j)
				arr[j--] = arr[i];
		}
		arr[i] = flag;
		return i;
	}

	public static void main(String[] args) {
		int[] arr = { 5, 10, 8, 9, 4, 3, 1, 6, 7, 2 };
		quicksort(arr, 0, arr.length - 1);
		for (int k = 0; k < arr.length; k++)
			System.out.print(arr[k] + " ");
	}
}

基数排序

基本思想：按顺序先排列某一个属性，如扑克牌的花色。（图片转自这里）

代码如下

package com.sort;
public class RadixSort {
	// pos=1表示个位，pos=2表示十位...
	public static int getNumInPos(int num, int pos) {
		int tmp = 1;
		for (int i = 0; i < pos - 1; i++) {
			tmp *= 10;
		}
		return (num / tmp) % 10;
	}
	// 求得最大位数d
	public static int getMaxWeishu(int[] a) {
		int max = a[0];
		for (int i = 0; i < a.length; i++) {
			if (a[i] > max)
				max = a[i];
		}
		int tmp = 1, d = 1;
		while (true) {
			tmp *= 10;
			if (max / tmp != 0) {
				d++;
			} else
				break;
		}
		return d;
	}
	public static void radixsort(int[] a, int d) {
		int[][] array = new int[10][a.length + 1];
		for (int i = 0; i < 10; i++) {
			array[i][0] = 0;// array[i][0]记录第i行数据的个数
		}
		for (int pos = 1; pos <= d; pos++) {
			for (int i = 0; i < a.length; i++) {// 分配过程
				int row = getNumInPos(a[i], pos);
				int col = ++array[row][0];
				array[row][col] = a[i];
			}
			for (int row = 0, i = 0; row < 10; row++) {// 收集过程
				for (int col = 1; col <= array[row][0]; col++) {
					a[i++] = array[row][col];
				}
				array[row][0] = 0;// 复位，下一个pos时还需使用
			}
		}
	}
	public static void main(String[] args) {
		int[] arr = { 49, 38, 65, 197, 76, 213, 27, 50, 4 };
		radixsort(arr, getMaxWeishu(arr));
		for (int k = 0; k < arr.length; k++)
			System.out.print(arr[k] + " ");
	}
}

选择排序

基本思想：第一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，然后再从剩余的未排序元素中寻找到最小（大）元素，然后放到已排序的序列的末尾。以此类推，直到全部待排序的数据元素的个数为零。选择排序是不稳定的排序方法。（图片转自这里）

代码如下：

package com.sort;

public class SelectSort {
	public static void selectsort(int[] arr) {
		int n = arr.length;
		for (int i = 0; i < n; i++) {
			int k = i;
			// 找出最小值的下标
			for (int j = i + 1; j < n; j++) {
				if (arr[j] < arr[k]) {
					k = j;
				}
			}
			// 将最小值放到未排序记录的第一个位置
			if (k > i) {
				int tmp = arr[i];
				arr[i] = arr[k];
				arr[k] = tmp;
			}
			for (int l = 0; l < arr.length; l++)
				System.out.print(arr[l] + " ");
			System.out.println();
		}
	}

	public static void main(String[] args) {
		int[] arr = { 5, 10, 8, 9, 4, 3, 1, 6, 7, 2 };
		selectsort(arr);
		for (int k = 0; k < arr.length; k++)
			System.out.print(arr[k] + " ");
	}
}

希尔排序

基本思想：希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。（图片转自这里）

代码如下：

package com.sort;

public class ShellSort {
	private static int items = 2;// 增量变大的时候会有问题
	public static void shellsort(int arr[]) {
		int n = arr.length;
		if (n <= 1)
			return;
		int gapNum = n / items;
		while (gapNum >= 1) {
			for (int i = 0; i < n; i++) {
				for (int j = i; j < n - gapNum; j = j + gapNum) {
					if (arr[j] > arr[j + gapNum]) {
						int temp = arr[j];
						arr[j] = arr[j + gapNum];
						arr[j + gapNum] = temp;
					}
				}
			}
			gapNum = gapNum / items;
		}
	}
	public static void main(String[] args) {
		int[] arr = { 10, 5, 8, 9, 3, 1, 6, 7, 2 };
		shellsort(arr);
		for (int k = 0; k < arr.length; k++)
			System.out.print(arr[k] + " ");
	}
} 

算法比较

应用场景

• 冒泡排序：优化后的冒泡排序可用于当数据已经基本有序，且数据量较小时；
• 插入排序：若数组基本有序且数据规模较小时，选用插入排序较好；
• 希尔排序：数据量较小且基本有序时；
• 选择排序：当数据规模较小时，选择排序性能较好；
• 堆排序：堆排序适合处理数据量大的情况，数据呈流式输入时用堆排序也很方便；
• 归并排序：数据量较大且要求排序稳定时；
• 快速排序：快速排序适合处理大量数据排序时的场景；
• 基数排序：基数排序虽然时间复杂度较低，但需要满足的条件较多，如果能满足限制条件与空间需求，基数排序自然很快。