Tensorflow快餐教程(7) - 梯度下降

梯度下降

学习完基础知识和矩阵运算之后，我们再回头看下第一节讲的线性回归的代码：

import tensorflow as tf
import numpy as np

trX = np.linspace(-1, 1, 101)
trY = 2 * trX + np.random.randn(*trX.shape) * 0.33 # 创建一些线性值附近的随机值

X = tf.placeholder("float") 
Y = tf.placeholder("float")

def model(X, w):
    return tf.multiply(X, w) # X*w线性求值，非常简单

w = tf.Variable(0.0, name="weights") 
y_model = model(X, w)

cost = tf.square(Y - y_model) # 用平方误差做为优化目标

train_op = tf.train.GradientDescentOptimizer(0.01).minimize(cost) # 梯度下降优化

# 开始创建Session干活！
with tf.Session() as sess:
    # 首先需要初始化全局变量，这是Tensorflow的要求
    tf.global_variables_initializer().run()

    for i in range(100):
        for (x, y) in zip(trX, trY):
            sess.run(train_op, feed_dict={X: x, Y: y})

    print(sess.run(w)) 

除了这一句

train_op = tf.train.GradientDescentOptimizer(0.01).minimize(cost)

应该都可以看懂了。
我们这一节就来讲看不懂的这一行，梯度下降优化函数。

从画函数图形说起

所谓梯度下降，其实没有什么神秘的，就是求个函数极值问题而己。
函数比矩阵强的一点是可以画图啊。

所以我们先学习一下如何画函数的图形：

import matplotlib.pyplot as plt
import numpy as np

x = np.linspace(-10,10,1000)
y = x ** 2 - 2 * x+ 1
plt.plot(x, y)
plt.title("matplotlib")
plt.xlabel("height")
plt.ylabel("width")
# 设置图例
plt.legend(["X","Y"], loc="upper right")
plt.grid(True)
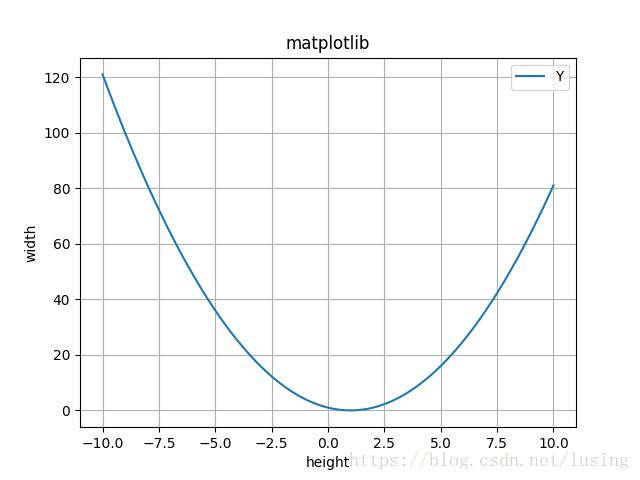
plt.show()

上面我们用np.linspace来生成若干点组成的向量，然后取 y=x2−2x+1 y = x 2 − 2 x + 1 的值。
画出的图像是这样的：

求函数的最小值

现在我们想要求这条曲线上的最小值点。因为这个函数的定义域是无限的，我们不可能从负无穷到正无穷挨个试那个最小。
但是，我们可以随便找一个点为起点，然后比较一下它左边相邻一点的点和右边和它相邻一点的点看看哪个更小。然后取较小的那个点，继续这个过程。

假设我们从x=-5这个坐标开始，y=(-5)(-5)-2(-5)+1=36。所以这个点是(-5,36).
我们取0.1为步长，看看-5.1和-4.9的y值是多少，发现同(-5.1, 37.21)和(-4.9,34.81)。-4.9的值更小，于是-4.9就成为新一轮迭代的值。然后从(-4.9,34.81)到(-4.8,33.64)，以此类推。一直到(1.0, 0)达到最小值，左右都比它大，这个极值就找到了。
求极值的这个函数我们称为损失函数loss function，或代价函数cost function，或者误差函数error function。这几个名称可以互换使用。
求得的极小值，我们称为 x∗=argminf(x) x ∗ = a r g m i n f ( x )

这种方法可以解决问题。但是它的问题在于慢。在函数下降速度很快的时候可以多移动一点加快速度，下降速度变慢了之后少移一点防止跑过了。

那么这个下降速度如何度量呢？我们都学过，用导数-derivative，也就是切线的斜率。有了导数之后，我们可以沿着导数的反方向，也就是切换下降的方向去寻找即可。
这种沿着x的导数的反方向移动一小步来减少f(x)值的技术，就被称为梯度下降 - gradient descent.
第n+1的值为第n次的值减去导数乘以一个可以调整的系数。
也就是
xn+1=xn−ηdf(x)dx x n + 1 = x n − η d f ( x ) d x
其中，这个可调整的系数 η η ，我们称为学习率。学习率越大下降速度越快，但是也可能错过最小值而产生振荡。
选择学习率的方法一般是取一个小的常数。也可以通过计算导数消失的步长。还可以多取几个学习率值，然后取效果最好的一个。

f(x)=x2−2x+1 f ( x ) = x 2 − 2 x + 1 的导函数为 f′(x)=2x−2 f ′ ( x ) = 2 x − 2
我们还是选择从(-5,36)这个点为起点，学习率我们取0.1。
则下一个点 x2=−5−0.1∗（2∗（−5）−2）=−3.8 x 2 = − 5 − 0.1 ∗ （ 2 ∗ （ − 5 ） − 2 ） = − 3.8
则第2个点下降到(-3.8,23.04)。比起第一种算法我们右移0.1，这次一下子就右移了1.2,效率提升12倍。

晋阶三维世界

我们看下我们在做线性回归时使用的损失函数：

cost = tf.square(Y - y_model)

这是个平方函数 fLoss=Σni=1(yi−(wxi+b))2 f L o s s = Σ i = 1 n ( y i − ( w x i + b ) ) 2
其中 yi y i 是已知的标注好的结果， xi x i 是已知的输入值。未知数只有两个，w和b。
所以下一步求梯度下降的问题变成求二元二次函数极小值的问题。

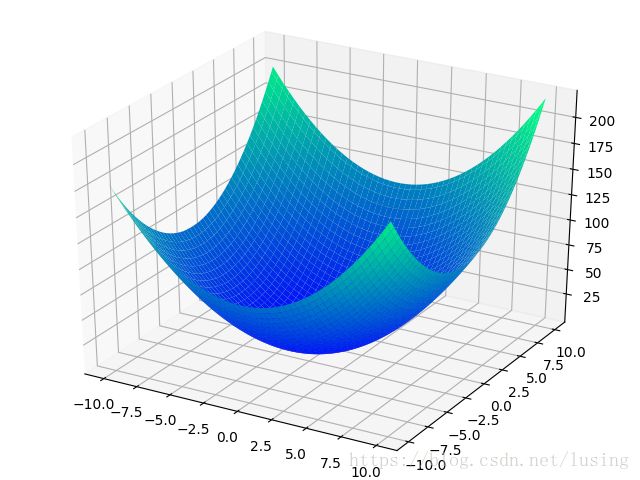
我们还是先看图，二元二次函数的图是什么样子的。我们取个 f(x,y)=x2+y2+x+y+1 f ( x , y ) = x 2 + y 2 + x + y + 1 为例吧。

先学画图：

from mpl_toolkits.mplot3d import Axes3D
import numpy as np
import matplotlib.pyplot as plt

# 创建 3D 图形对象
fig = plt.figure()
ax = Axes3D(fig)

X3 = np.linspace(-10,10,100)
Y3 = np.linspace(-10,10,100)
X3, Y3 = np.meshgrid(X3, Y3)
Z3 = X3*X3 + Y3*Y3 + X3 + Y3 + 1
ax.plot_surface(X3, Y3, Z3, cmap=plt.cm.winter)

# 显示图
plt.show()

图绘制出来是这样子的：

从一条曲线变成了一个碗一样的曲面。但是仍然是有最小值点的。

现在不只是有x一个方向，而是有x和y两个方向。两个方向也好办，x方向和y方向分别找梯度就是了。分别取x和y方向的偏微分。
xn+1=xn−η∂f(x,y)∂x,yn+1=yn−η∂f(x,y)∂y x n + 1 = x n − η ∂ f ( x , y ) ∂ x , y n + 1 = y n − η ∂ f ( x , y ) ∂ y

偏导数虽然从 d d 换成了 ∂ ∂ ，但是求微分的公式还是一样的。只不过在求x的时候把y当成常数就是了。

我们可以用梯度符号来简单表示 ∇=(∂f(x,y)∂x,∂f(x,y)∂y) ∇ = ( ∂ f ( x , y ) ∂ x , ∂ f ( x , y ) ∂ y ) ，这个倒三角符号读作nabla.

在Tensorflow里，梯度下降这样基本的操作自然是不需要我们操心的，我们只需要调用tf.train.GradientDescentOptimizer就好。

例子我们在前面已经看过了，我们复习一下：

cost = tf.square(Y - y_model) # 用平方误差做为优化目标

train_op = tf.train.GradientDescentOptimizer(0.01).minimize(cost) # 梯度下降优化

赋给GradientDescentOptimizer的0.01就是我们的 η η ，学习率。

自适应梯度演化史

如果您的逻辑思维比较强的话，一定会发现从二维导数升级到三维梯度时，有一个参数我们没有跟着一起扩容，那就是学习率 η η .

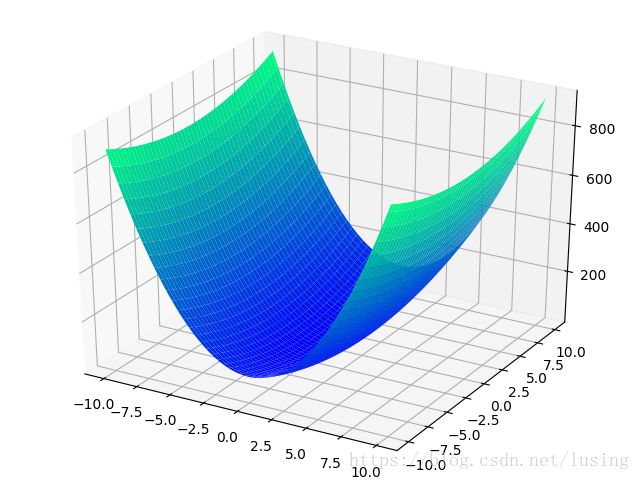
我们还是看一个图，将上面的方程变成 f(x,y)=8x2+y2+x+y+1 f ( x , y ) = 8 x 2 + y 2 + x + y + 1

Z3 = 8*X3*X3 + Y3*Y3 + X3 + Y3 + 1

图像变成下面这样子：

大家可以直观地感受到， ∂f(x,y)∂x ∂ f ( x , y ) ∂ x 和 ∂f(x,y)∂y ∂ f ( x , y ) ∂ y 方向的下降速度是明显不一样的。
如果对于更高维的情况，问题可能更严重，众口难调。

最简单的方法可能是对于每个维度都用一个专门的学习率。不过这样也太麻烦了，这时Adaptive Gradient自适应梯度下降就被当时在UC伯克利读博士的John C. Duchi提出了，简写为AdaGrad.
在Tensorflow中，我们可以通过tf.train.AdagradOptimizer来使用AdaGrad.

AdaGrad的公式为 (xt+1)i=(xt)i−ηΣtτ=1(∇f(xτ))2i√(∇f(xt))i ( x t + 1 ) i = ( x t ) i − η Σ τ = 1 t ( ∇ f ( x τ ) ) i 2 ( ∇ f ( x t ) ) i

但是，AdaGrad也有自己的问题。虽然初始指定一个 η η 值之后可以自适应，但是如果这个 η η 太大的话仍然会导致优化不稳定。但是如果太小了，随着优化，这个学习率会越来越小，可能就到不了极小值就停下来了。

于是当时在Google做实习生的Mathew Zeiler做出了两点改进：一是引入时间窗口概念，二是不用手动指定学习率。改进之后的算法叫做AdaDelta.
公式中用到的RMS是指Root Mean Square，均方根.
AdaDelta的公式为 (∇xi)i=−(RMS[Δx]t−1)i(RMS[g]t)i(∇f(xi))i ( ∇ x i ) i = − ( R M S [ Δ x ] t − 1 ) i ( R M S [ g ] t ) i ( ∇ f ( x i ) ) i
具体过程请看Zeiler同学写的paper: http://arxiv.org/pdf/1212.5701v1.pdf

在Tensorflow中，我们只要使用tf.train.AdadeltaOptimizer这个封装就好。

AdaDelta并不是唯一的改进方案，类似的方案还有RMSProp, Adam等。我们可以使用tf.train.RMSPropOptimizer和tf.train.AdamOptimizer来调用就好了。

还记得第1节中我们讲卷积神经网络的例子吗？我们用的不再是梯度下降，而是RMSProp：

cost = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(logits=py_x, labels=Y))
train_op = tf.train.RMSPropOptimizer(0.001, 0.9).minimize(cost)
predict_op = tf.argmax(py_x, 1)

物理学的启示

虽然各种自适应梯度下降方法洋洋大观，但是复杂的未必就是最好的。导数的物理意义可以认为是速度。速度的变化我们可以参考物理学的动量的概念，同时引入惯性的概念。如果遇到坑，靠动量比较容易冲出去，而其它方法就要迭代很久。
在Tensorflow中，可以通过tf.train.MomentumOptimizer来使用动量方法。

我们可以看一下Mathew Zeiler的论文中对于几种方法的对比：

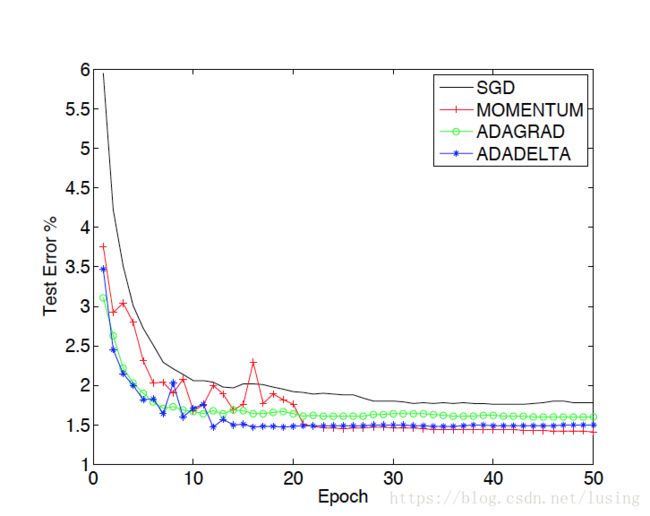
从中可以看到，虽然在前期，动量方法上窜下跳不像AdaGrad稳定，但是后期效果仍然是最好的。