PyTorch: Softmax多分类实战

多分类一种比较常用的做法是在最后一层加softmax归一化，值最大的维度所对应的位置则作为该样本对应的类。本文采用PyTorch框架，选用经典图像数据集mnist学习一波多分类。

MNIST数据集

MNIST 数据集(手写数字数据集)来自美国国家标准与技术研究所, National Institute of Standards and Technology (NIST). 训练集 (training set) 由来自 250 个不同人手写的数字构成, 其中 50% 是高中学生, 50% 来自人口普查局 (the Census Bureau) 的工作人员. 测试集(test set) 也是同样比例的手写数字数据。MNIST数据集下载地址:http://yann.lecun.com/exdb/mnist/。手写数字的MNIST数据库包括60,000个的训练集样本，以及10,000个测试集样本。

其中：
train-images-idx3-ubyte.gz (训练数据集图片)
train-labels-idx1-ubyte.gz （训练数据集标记类别）
t10k-images-idx3-ubyte.gz: （测试数据集）
t10k-labels-idx1-ubyte.gz（测试数据集标记类别）

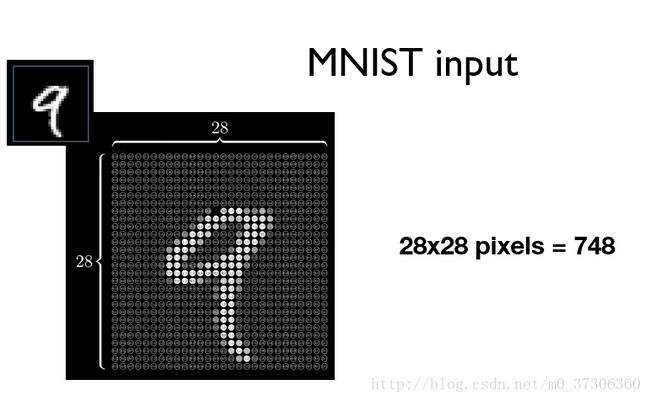
MNIST数据集是经典图像数据集，包括10个类别(0到9)。每一张图片拉成向量表示，如下图784维向量作为第一层输入特征。

Softmax分类

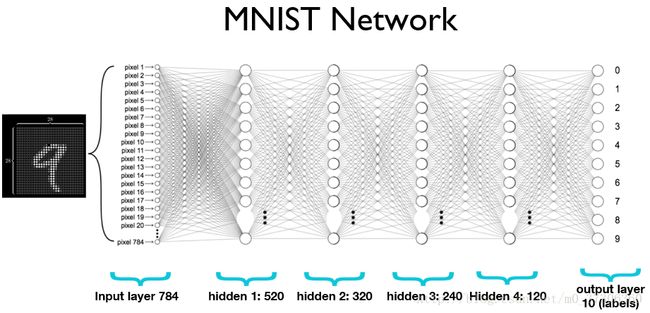
softmax函数的本质就是将一个K 维的任意实数向量压缩（映射）成另一个K维的实数向量，其中向量中的每个元素取值都介于（0，1）之间，并且压缩后的K个值相加等于1(变成了概率分布)。在选用Softmax做多分类时，可以根据值的大小来进行多分类的任务，如取权重最大的一维。softmax介绍和公式网上很多，这里不介绍了。下面使用Pytorch定义一个多层网络(4个隐藏层，最后一层softmax概率归一化)，输出层为10正好对应10类。

PyTorch实战

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
from torch.autograd import Variable

# Training settings
batch_size = 64

# MNIST Dataset
train_dataset = datasets.MNIST(root='./mnist_data/',
                               train=True,
                               transform=transforms.ToTensor(),
                               download=True)

test_dataset = datasets.MNIST(root='./mnist_data/',
                              train=False,
                              transform=transforms.ToTensor())

# Data Loader (Input Pipeline)
train_loader = torch.utils.data.DataLoader(dataset=train_dataset,
                                           batch_size=batch_size,
                                           shuffle=True)

test_loader = torch.utils.data.DataLoader(dataset=test_dataset,
                                          batch_size=batch_size,
                                          shuffle=False)


class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.l1 = nn.Linear(784, 520)
        self.l2 = nn.Linear(520, 320)
        self.l3 = nn.Linear(320, 240)
        self.l4 = nn.Linear(240, 120)
        self.l5 = nn.Linear(120, 10)

    def forward(self, x):
        # Flatten the data (n, 1, 28, 28) --> (n, 784)
        x = x.view(-1, 784)
        x = F.relu(self.l1(x))
        x = F.relu(self.l2(x))
        x = F.relu(self.l3(x))
        x = F.relu(self.l4(x))
        return F.log_softmax(self.l5(x), dim=1)
        #return self.l5(x)

model = Net()

optimizer = optim.SGD(model.parameters(), lr=0.01, momentum=0.5)

def train(epoch):
    # 每次输入barch_idx个数据
    for batch_idx, (data, target) in enumerate(train_loader):
        data, target = Variable(data), Variable(target)

        optimizer.zero_grad()
        output = model(data)
        # loss
        loss = F.nll_loss(output, target)
        loss.backward()
        # update
        optimizer.step()
        if batch_idx % 200 == 0:
            print('Train Epoch: {} [{}/{} ({:.0f}%)]\tLoss: {:.6f}'.format(
                epoch, batch_idx * len(data), len(train_loader.dataset),
                100. * batch_idx / len(train_loader), loss.data[0]))

def test():
    test_loss = 0
    correct = 0
    # 测试集
    for data, target in test_loader:
        data, target = Variable(data, volatile=True), Variable(target)
        output = model(data)
        # sum up batch loss
        test_loss += F.nll_loss(output, target).data[0]
        # get the index of the max
        pred = output.data.max(1, keepdim=True)[1]
        correct += pred.eq(target.data.view_as(pred)).cpu().sum()

    test_loss /= len(test_loader.dataset)
    print('\nTest set: Average loss: {:.4f}, Accuracy: {}/{} ({:.0f}%)\n'.format(
        test_loss, correct, len(test_loader.dataset),
        100. * correct / len(test_loader.dataset)))

for epoch in range(1,6):
    train(epoch)
    test()


输出结果：
Train Epoch: 1 [0/60000 (0%)]   Loss: 2.292192
Train Epoch: 1 [12800/60000 (21%)]  Loss: 2.289466
Train Epoch: 1 [25600/60000 (43%)]  Loss: 2.294221
Train Epoch: 1 [38400/60000 (64%)]  Loss: 2.169656
Train Epoch: 1 [51200/60000 (85%)]  Loss: 1.561276

Test set: Average loss: 0.0163, Accuracy: 6698/10000 (67%)

Train Epoch: 2 [0/60000 (0%)]   Loss: 0.993218
Train Epoch: 2 [12800/60000 (21%)]  Loss: 0.859608
Train Epoch: 2 [25600/60000 (43%)]  Loss: 0.499748
Train Epoch: 2 [38400/60000 (64%)]  Loss: 0.422055
Train Epoch: 2 [51200/60000 (85%)]  Loss: 0.413933

Test set: Average loss: 0.0065, Accuracy: 8797/10000 (88%)

Train Epoch: 3 [0/60000 (0%)]   Loss: 0.465154
Train Epoch: 3 [12800/60000 (21%)]  Loss: 0.321842
Train Epoch: 3 [25600/60000 (43%)]  Loss: 0.187147
Train Epoch: 3 [38400/60000 (64%)]  Loss: 0.469552
Train Epoch: 3 [51200/60000 (85%)]  Loss: 0.270332

Test set: Average loss: 0.0045, Accuracy: 9137/10000 (91%)

Train Epoch: 4 [0/60000 (0%)]   Loss: 0.197497
Train Epoch: 4 [12800/60000 (21%)]  Loss: 0.234830
Train Epoch: 4 [25600/60000 (43%)]  Loss: 0.260302
Train Epoch: 4 [38400/60000 (64%)]  Loss: 0.219375
Train Epoch: 4 [51200/60000 (85%)]  Loss: 0.292754

Test set: Average loss: 0.0037, Accuracy: 9277/10000 (93%)

Train Epoch: 5 [0/60000 (0%)]   Loss: 0.183354
Train Epoch: 5 [12800/60000 (21%)]  Loss: 0.207930
Train Epoch: 5 [25600/60000 (43%)]  Loss: 0.138435
Train Epoch: 5 [38400/60000 (64%)]  Loss: 0.120214
Train Epoch: 5 [51200/60000 (85%)]  Loss: 0.266199

Test set: Average loss: 0.0026, Accuracy: 9506/10000 (95%)

Process finished with exit code 0

随着训练迭代次数的增加，测试集的精确度还是有很大提高的。并且当迭代次数为5时，使用这种简单的网络可以达到95%的精确度。