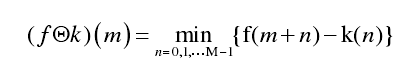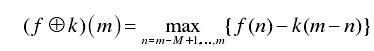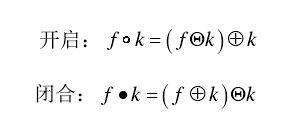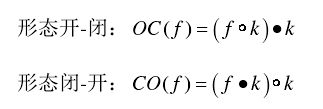心电信号去噪3--数学形态学

本系列上一篇(中值滤波器)指路：https://blog.csdn.net/m0_37422217/article/details/90739660

注：这里是以小型手持心电图机为研究对象的(单导联)

 

上一篇中我们说到中值滤波器可以较好的去除基线漂移的噪音,此外数学形态学也可以很好的去除基线漂移，并且数学形态法也可以去除其他类型的噪音。

 

数学形态法原理

数学形态学是一门建立在严格数学理论基础上的学科,它提供了一种有效的非线性信号处理方法,可以很好地保持信号的几何信息。数学形态学最基本的概念是结构元素,它本身具有一定的形态(如点、线段和圆等),相当于一个`探针',

在图形中不断地移动结构元素,便可考察出图形各部分间的关系,类似于人的注意焦点(focus of attention,FOA)视觉特点,结构元素可直接携带图形知识(形态、大小等)。用不同的结构元素来处理一维信号可以得出不同的结果.[1]

腐蚀和膨胀是数学形态学中最基本的运算,其定义如下：

设信号序列 f 为定义在 F={0，1，…，N-1}上的序列函数，结构元素 k 为定义在 K={0，1，…，M-1}上的函数，其中 N>M，那么结构元素 k 对信号 f 的腐蚀运算可以定义为：
 

 其中 m=0，1，…，N-M。

结构元素 k 对信号 f 的膨胀运算可以定义为：

其中 m=M-1，M-2，…，N-1。

信号 f 被膨胀的结果就是把结构元素 k 平移后使集合 K 与集合 F 交集非空点构成的集合，其作用效果是集合 F 呈现出的图像扩大了。而腐蚀的结果就是把结构元素 k 平移后，使集合 K 包含于集合 F 交集所有点构成的集合，其作用效果是使集合 F 呈现出的图像缩小。

膨胀和腐蚀运算还可以组成开（opening，）、闭（closing，•）、击中、薄化、厚化等几种运算方式。其中开（opening，）、闭（closing，•）的定义为：

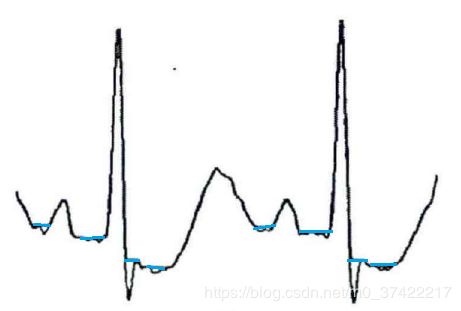
数学形态学理论认为，开运算和闭运算分别是在信号的下方和上方移动结构元素。开运算可以削除信号“波峰”，具有收缩性，消除信号孤立点，抑制正脉冲噪声，使信号光滑；闭运算则可以填充信号的“波谷”，具有扩张性，可抑制负脉冲噪声。开闭运算均具有低通特性。

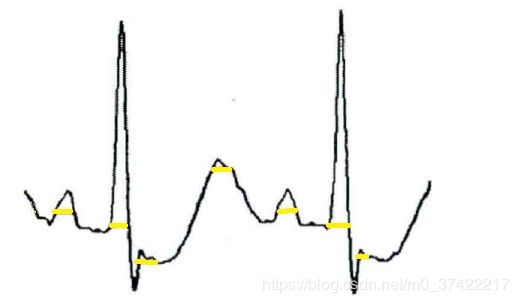
以下，分别给出开、闭运算对一段ECG信号进行处理结果:

黑色线为原始心电信号，黄色线为开运算对心电信号的处理结果，可以看出开运算削除了信号“波峰”：

 

同样，黑色线为原始心电信号，蓝色线为闭运算对心电信号的处理结果，可以看出开运算填充了信号“波谷”：

 

PS:原作者用细实线组成的波形均代表原始心电信号，粗实线构成的波形代表开、闭运算处理后的心电信号，但是我实在是有点看不清粗细，就给他用不同颜色表示了。。。。

形态滤波器的实质是通过组合运用开、闭运算,消除信号中特定宽度的波峰和波谷。信号中实际被滤除的成分与运算中所采用的结构元素有关,如结构元素的宽度为M,信号中波峰或波谷的宽度为N,则有:
 

 

为了可同时去除信号中的正负两种脉冲噪声,Maragos采用开、闭运算的级联组合形式,定义了形态开闭(open-closing)和闭开(close-opening)滤波器:
 

由于开运算的收缩性导致形态开-闭滤波的输出偏小，闭运算的扩张性又导致形态闭-开滤波的输出偏小，很大程度上影响了滤波器高效去除噪声的性能，所以为减少偏移的发生，取得较好的滤波效果，我们并不单一地使用它们，而是通过形态开-闭和形态闭-开级联对信号进行滤波，设信号为f，则通过形态学滤波后的数学表达式为：

 

结构元素

结构元素是数学形态学滤波器中的一个非常重要的参数，在心电信号预处理领域中，它的形状、宽度和高度决定着滤波的效果。

(1)形状:选取的结构元素的形状要尽可能接近待分析信号的图形特点。结构元素有一些不同的形状,如三角形、圆形和直线形等。

(2)尺寸:结构元素的尺寸包括宽度(结构元素定义域的宽度)和高度(结构元素的幅值)。其中结构元素的宽度对信号的处理效果影响更大。选取结构元素的尺寸应大于被滤除信号的尺寸,但小于被保留信号的尺寸。若选取的宽度较大,则可能会滤除特征波形,引起失真,若宽度较小,则不能完全滤除噪声。
 

实例1

这里我们采取直线型结构元素的数学形态学滤波器，直线型结构元素的宽度应大于心电特征波形的宽度，使得这些特征波形都被滤除，只剩下基线漂移信号，再用原信号减去获得的基线干扰信号，即可获得滤除了基线漂移干扰后的心电信号。这里我取宽度M=65(特征波形最大宽度*采样频率)

代码：

% x 为原始信号
% 关于strel函数的具体用法，请见:https://blog.csdn.net/qwerasdf_1_2/article/details/54376657

se1 = strel('line', 65, 0); %设置为线性,长度为65,角度为0
fo1 = imopen(x, se1);%开运算
fc1 = imclose(x, se1);%闭运算
foc1 = imclose(fo1, se1); %开-闭运算
fco1 = imopen(fc1, se1);%闭-开元算
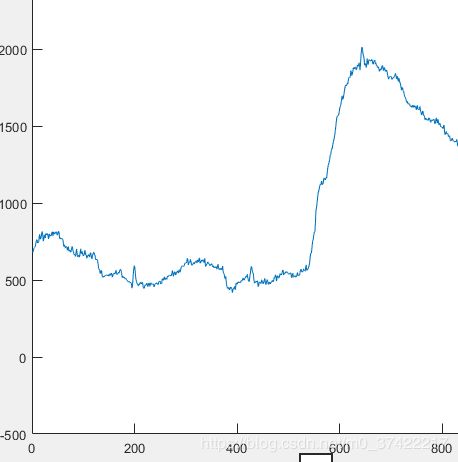
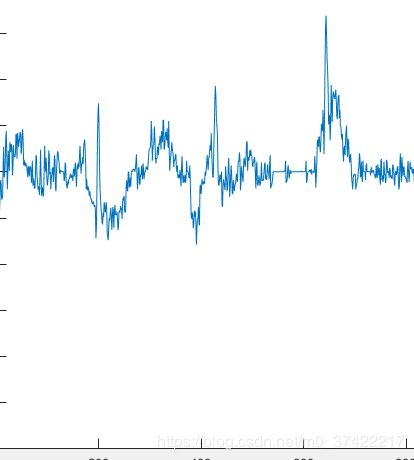
x =  x - floor((foc1 + fco1)/2);

原始信号：

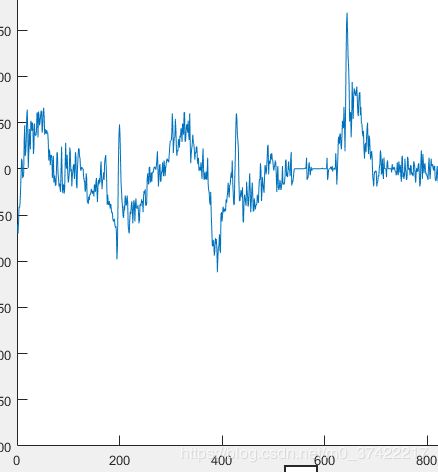
处理后信号：

.。。。。。嗯。。。感觉有点一言难尽呀

 

实例2

也有参考文献指出，可以先利用第一组形态滤波模块，提取心电信号中的QRS波群；再利用第二组形态滤波模块在第一组的基础上，提取P波和T波，最后将两者加总，就可以剔除基线漂移产生的噪音了。我们试一试：同样选取直线型结构元素的数学形态学滤波器，第一组结构序列宽度M1= 25，第二组结构序列宽度M2 = 65。

代码：

seA = strel('line', 25, 0); %设置为线性,长度为25,角度为0  
fo = imopen(x, seA);
fc = imclose(x, seA);
foc = imclose(fo, seA); 
fco = imopen(fc, seA);
xb2 = floor((foc + fco)/2);
QRSx = x - xb2; %QRS波提取

seB = strel('line', 65, 0); %设置为线性,长度为65,角度为0 
fo = imopen(xb2, seB);
fc = imclose(xb2, seB);
foc = imclose(fo, seB); 
fco = imopen(fc, seB);
xc = floor((foc + fco)/2);        
TPx = xb2- xc;  % P波 T波提取
x = QRSx + TPx;

处理后信号：

 

 

看起来，好像比例1稍微好一点。。。。。吧

主要参考文献:
[1]基于形态学滤波器的ECG信号预处理

[2]基于FIR滤波和数学形态学的心电信号预处理算法
[3]ECG去噪和Ｒ波检测的算法研究

[4]心电信号去噪的数学形态学滤波器

[5]基于 EMD 的心电信号去噪方法研究及实现

下一篇(EMD)指路：https://blog.csdn.net/m0_37422217/article/details/90922047