基于Python遗传算法的人工神经网络优化
人工神经网络(ANN)是一种简单的全连接神经网络,其通过前向传播来进行参数计算,使用后向传播进行参数权重更新。一般我们会采用随机梯度下降来更新权重,但今天我们换一个新的方法,通过遗传算法来进行参数寻优,遗传算法是一种经典的优化算法,其算法思想借鉴生物种群间“优胜劣汰”的机制。在本例程中我们通过使用遗传算法优化人工神经网络权重进行图像分类实验。
“
项目地址:
https://github.com/ahmedfgad/NeuralGenetic
”
确定待优化参数
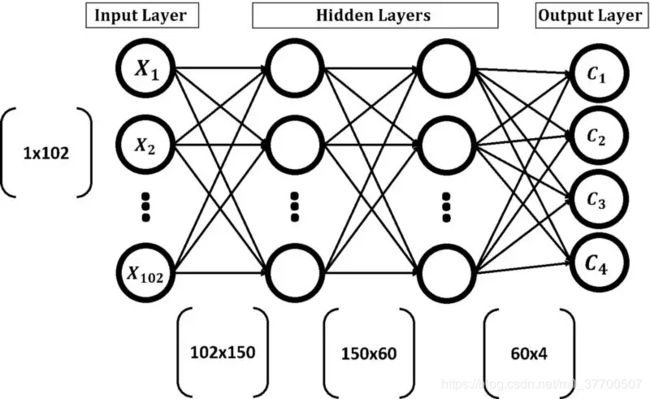
本例中,我们将要通过遗传算法优化神经网络各层的网络参数,因此我们首先定义人工神经网络的网络结构,这里我们使用的是4层网络,即一个输入、2个隐藏、1个输出。那么我们就得到要优化参数个数为102x150 + 150x60 + 60x4 = 24540个,如果我们设定遗传算法有8个群体,即整个参数数量将有24540x8 = 196320个。
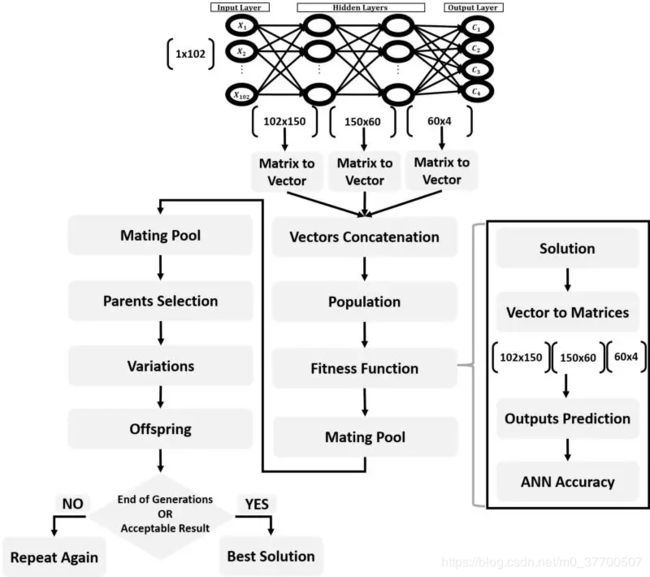
由于网络的参数是矩阵形式,而在GA中是矢量形式,所以我们在优化的过程中需要转换以方便计算。下图是整个案例的流程图:
代码部分函数介绍
mat_to_vector函数和vector_to_mat函数:因为GA中参数为一维向量,而在ANN中是3个权重矩阵,所以通过这两个函数进行相互转换。
mat_to_vector函数代码如下
def mat_to_vector(mat_pop_weights):
pop_weights_vector = []
for sol_idx in range(mat_pop_weights.shape[0]):
curr_vector = []
for layer_idx in range(mat_pop_weights.shape[1]):
vector_weights = numpy.reshape(mat_pop_weights[sol_idx, layer_idx], newshape=(mat_pop_weights[sol_idx, layer_idx].size))
curr_vector.extend(vector_weights)
pop_weights_vector.append(curr_vector)
return numpy.array(pop_weights_vector)
vector_to_mat函数代码如下
def vector_to_mat(vector_pop_weights, mat_pop_weights):
mat_weights = []
for sol_idx in range(mat_pop_weights.shape[0]):
start = 0
end = 0
for layer_idx in range(mat_pop_weights.shape[1]):
end = end + mat_pop_weights[sol_idx, layer_idx].size
curr_vector = vector_pop_weights[sol_idx, start:end]
mat_layer_weights = numpy.reshape(curr_vector, newshape=(mat_pop_weights[sol_idx, layer_idx].shape))
mat_weights.append(mat_layer_weights)
start = end
return numpy.reshape(mat_weights, newshape=mat_pop_weights.shape)
predict_outputs()函数:根据当前权重计算方案的准确度,而且在该函数中我们需要指定激活函数:relu或sigmod。
def predict_outputs(weights_mat, data_inputs, data_outputs, activation="relu"):
predictions = numpy.zeros(shape=(data_inputs.shape[0]))
for sample_idx in range(data_inputs.shape[0]):
r1 = data_inputs[sample_idx, :]
for curr_weights in weights_mat:
r1 = numpy.matmul(a=r1, b=curr_weights)
if activation == "relu":
r1 = relu(r1)
elif activation == "sigmoid":
r1 = sigmoid(r1)
predicted_label = numpy.where(r1 == numpy.max(r1))[0][0]
predictions[sample_idx] = predicted_label
correct_predictions = numpy.where(predictions == data_outputs)[0].size
accuracy = (correct_predictions/data_outputs.size)*100
return accuracy, predictions
fitness()函数:将每个方案解循环传给predict_outputs()函数计算结果,并将得到的准确度结果存储到数组中,
def fitness(weights_mat, data_inputs, data_outputs, activation="relu"):
accuracy = numpy.empty(shape=(weights_mat.shape[0]))
for sol_idx in range(weights_mat.shape[0]):
curr_sol_mat = weights_mat[sol_idx, :]
accuracy[sol_idx], _ = predict_outputs(curr_sol_mat, data_inputs, data_outputs, activation=activation)
return accuracy
完整Python编程结构
本案例共三个Python脚本文件,其中GA.py实现遗传算法功能;ANN.py实现ANN相应结构功能;main.py为项目主程序,包括读取数据特征和类标签文件,根据标准偏差过滤特征,创建ANN架构,生成初始解决方案,通过计算所有解决方案的适合度值,选择最佳父母,应用交叉和突变,最后创造新的群体。main.py程序如下:
import numpy
import GA
import pickle
import ANN
import matplotlib.pyplot
f = open("dataset_features.pkl", "rb")
data_inputs2 = pickle.load(f)
f.close()
features_STDs = numpy.std(a=data_inputs2, axis=0)
data_inputs = data_inputs2[:, features_STDs>50]
f = open("outputs.pkl", "rb")
data_outputs = pickle.load(f)
f.close()
#Genetic algorithm parameters:
# Mating Pool Size (Number of Parents)
# Population Size
# Number of Generations
# Mutation Percent
sol_per_pop = 8
num_parents_mating = 4
num_generations = 1000
mutation_percent = 10
#Creating the initial population.
initial_pop_weights = []
for curr_sol in numpy.arange(0, sol_per_pop):
HL1_neurons = 150
input_HL1_weights = numpy.random.uniform(low=-0.1, high=0.1,
size=(data_inputs.shape[1], HL1_neurons))
HL2_neurons = 60
HL1_HL2_weights = numpy.random.uniform(low=-0.1, high=0.1,
size=(HL1_neurons, HL2_neurons))
output_neurons = 4
HL2_output_weights = numpy.random.uniform(low=-0.1, high=0.1,
size=(HL2_neurons, output_neurons))
initial_pop_weights.append(numpy.array([input_HL1_weights,
HL1_HL2_weights,
HL2_output_weights]))
pop_weights_mat = numpy.array(initial_pop_weights)
pop_weights_vector = GA.mat_to_vector(pop_weights_mat)
best_outputs = []
accuracies = numpy.empty(shape=(num_generations))
for generation in range(num_generations):
print("Generation : ", generation)
# converting the solutions from being vectors to matrices.
pop_weights_mat = GA.vector_to_mat(pop_weights_vector,
pop_weights_mat)
# Measuring the fitness of each chromosome in the population.
fitness = ANN.fitness(pop_weights_mat,
data_inputs,
data_outputs,
activation="sigmoid")
accuracies[generation] = fitness[0]
print("Fitness")
print(fitness)
# Selecting the best parents in the population for mating.
parents = GA.select_mating_pool(pop_weights_vector,
fitness.copy(),
num_parents_mating)
print("Parents")
print(parents)
# Generating next generation using crossover.
offspring_crossover = GA.crossover(parents,
offspring_size=(pop_weights_vector.shape[0]-parents.shape[0], pop_weights_vector.shape[1]))
print("Crossover")
print(offspring_crossover)
# Adding some variations to the offsrping using mutation.
offspring_mutation = GA.mutation(offspring_crossover,
mutation_percent=mutation_percent)
print("Mutation")
print(offspring_mutation)
# Creating the new population based on the parents and offspring.
pop_weights_vector[0:parents.shape[0], :] = parents
pop_weights_vector[parents.shape[0]:, :] = offspring_mutation
pop_weights_mat = GA.vector_to_mat(pop_weights_vector, pop_weights_mat)
best_weights = pop_weights_mat [0, :]
acc, predictions = ANN.predict_outputs(best_weights, data_inputs, data_outputs, activation="sigmoid")
print("Accuracy of the best solution is : ", acc)
matplotlib.pyplot.plot(accuracies, linewidth=5, color="black")
matplotlib.pyplot.xlabel("Iteration", fontsize=20)
matplotlib.pyplot.ylabel("Fitness", fontsize=20)
matplotlib.pyplot.xticks(numpy.arange(0, num_generations+1, 100), fontsize=15)
matplotlib.pyplot.yticks(numpy.arange(0, 101, 5), fontsize=15)
f = open("weights_"+str(num_generations)+"_iterations_"+str(mutation_percent)+"%_mutation.pkl", "wb")
pickle.dump(pop_weights_mat, f)
f.close()
在进行迭代1000次训练之后,得到模型精度折线图如下,可以看到经过1,000次迭代后,精度超过97%,这个结果还是相当可以的。
欢迎关注公众号《深度学习与Python》,专注于深度学习、机器学习前沿知识与资讯