加密算法------DES加密算法详解

一、加密算法的分类

1.对称加解密算法

a.通信双方同时掌握一个密钥，加密解密都是由一个密钥完成的（即加密密钥等于解密密钥，加解密密钥可以相互推倒出来）。

b.双方通信前共同拟定一个密钥，不对第三方公开。

c.不具有个体原子性，一个密钥被共享，泄漏几率增大

2.公私钥加解密算法

a.通信双方掌握不同的密钥，不同方向的加解密由不同的密钥完成。

二、对称加密算法的代表----DES加密算法

原理：该算法是一个利用56+8奇偶校验位（第8,16,24,32,40,48,56,64）=64位的密钥对以64位为单位的块数据进行加解密。

具体过程：

    有明文M（64位） = 0123456789ABCDEF

        即M（64位） = 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

            L（32位） = 0000 0001 0010 0011 0100 0101 0110 0111

            R（32位） = 1000 1001 1010 1011 1100 1101 1110 1111

    有密钥64位：133457799BBCDFF1

        即K（64位） = 00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001

            注：其中红色为奇偶校验位，即实际密钥为56位

第一步：按照下表中的规则对各个位进行交换，生成16个子钥（48位）

交换规则表（8*7）：57      49       41        33        25         17          9

                              1          58       50       42        34          26         18

                               10        2         59       51        43         35          27

                                19        11        3        60        52         44          36

                                 63        55       47       39         31         23          15

                                  7          62       54       46         38         30           22

                                  14          6         61      53          45        37            29

                                  21          13        5        28         20         12             4

交换方法：第一行第一列的数为57，那么就将K中第一位上的数换成K中第57位上的数（将0换为了57位上的1），依次类推。

那么原K（64位） = 00010011 00110100 01010111 01111001 10011011 10111100 11011111 11110001

去掉奇偶校验位，再经过上表的转换就变为了：

     K + （56位） =  1111000  0110011  0010101  0101111  0101010   1011001    1001111  0001111

因此：C0（28位） = 1111000  0110011  0010101  0101111

          D0（28位） = 0101010   1011001    1001111  0001111

下来依次是C1,D1为C0,D0左移一位，C2,D2为C1,D1左移一位，C3,D3为C2,D2左移两位.......

所以，可以得到C1D1----C16D16的结果为：

C1 = 1110000 1100110 01010101011111

D1 = 1010101011001100111100011110

C2 = 1100001100110010101010111111

D2 = 0101010110011001111000111101

C3 = 0000110011001010101011111111

D3 = 0101011001100111100011110101

................

.................

C15 = 1111100001100110010101010111

D15 = 1010101010110011001111000111

C16 = 1111000011001100101010101111

D16 = 0101010101100101101110001111

Kn（48位） = PC-2（CnDn（56位））

PC-2（8*6）----为一个8*6的矩阵，将上面得到的16个子钥按照下表的规律进行位的交换

14        17        11       24        1        5

3           28       15        6         21      10

23          19       12       4          26      8

16           7         27      20         13     2

41           52        31     37          47     55

30            40        51    45           33    48

44            49        39     56          34     53

46             42        50     36          29     32

因此，通过上面公式的计算可以得到：

K1 = 000110 110000 001011 101111 111111 000111 000001 110010

（Eg：C1D1 = 1110000 1100110 0101010 1011111  1010101 0110011 0011110 0011110

红色部分为奇偶校验位，那么通过上表对C1D1进行位的变换：将14位上的0放到第一位，将17位上的0放到第二位，将11位上的0放到第三位，将24位上的1放到第四位，将1位上的一放到第五位，将5位上的0放到第六位；则最后的前6位的结果·就·变为000110，剩下的做法同上）

****************以下做法都同K1*********************************

K2 = 011110 011010 111011 011001 110110 111100 100111 100101

K3 = 010101 011111 110010 001010 010000 101100 111110 011001

K4 = 011100 101010 110111 010110 110110 110011 010100 011101

K5 = 011111 001110 110000 000111 111010 110101 001110 101000

K6 = 011000 111010 010100 111110 010100 000111 101100 101111

K7 = 111011 001000 010010 110111 111101 100001 100010 111100

K8 = 111101 111000 101000 111010 110000 010011 101111 111011

K9 = 111000 001101 101111 101011 111011 011110 011110 000001

K10 = 101100 011111 001101 000111 101110 100100 011001 001111

K11 = 001000 010101 111111 010011 110111 101101 001110 000110 

K12 = 011101 010111 000111 110101 100101 000110 011111 101001

K13 = 100101 111100 010111 010001 111110 101011 101001 000001

K14 = 010111 110100 001110 110111 111100 101110 011100 111010

K15 = 101111 111001 000110 001101 001111 010011 111100 001010

K16 = 110010 110011 110110 001011 000011 100001 011111 110101

因此，最终就得到了如上的16个子密钥，每个48位

第二步：用得到的子密钥对64位数据加密

对明文M使用IP（8*8）

58      50    42     34        26       18       10        2

60      52     44     36       28       20        12       4

62      54     46      38       30       22       14       6

64      56     48       40       32      24       16       8

57     49      41        33      25       17       9        1

59     51       43       35      27       19       11       3

61      53      45       37       29       21       13       5

63      55      47        39      31       23       15       7

因为： M（64位） = 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

对M进行IP操作可以得到：

            IP（64位） = 1100 1100 0000 0000 1100 1100 1111 1111 11111 0000 1010 1010 1111 0000 1010 1010

            IP（64位） = L0（32位）+ R0（32位）

             L0（32位） = 1100 1100 0000 0000 1100 1100 1111 1111

             R0（32位） = 11111 0000 1010 1010 1111 0000 1010 1010

接下来，从L0和R0开始，循环16次根据递推公式

得出L1R1到L16R16。其中除了Kn为48位，其它变量及函数均为32位。

得到L1R1到L16R16的具体过程如下：

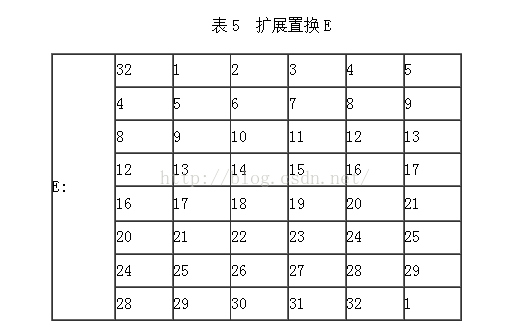
1.将数据的右半部分R0通过扩展置换E从32位扩展到48位

    通过将原32位数据中的某些位重复出现达到扩展的目的。扩展置换也称位选择函数，俗称E盒，扩展置换E通过将第32，1,4,5,8,9,12,13,16,17,20,21,24,25,28,29共16位分别放置在两个位置，从而将32位的数据扩展为48位。

根据上面的E表则扩展之后的R0为：

 原来的： R0（32位） = 1111 0000 1010 1010 1111 0000 1010 1010

 扩展后： R0（64位） = 011110 100001 010101 010101 011110 100001 010101 010101

然后将R0（64位）与

                K1（64位） =  000110 110000 001011 101111 111111 000111 000001 110010做异或运算

得到结果为：E（R（n-1）异或K1） = 011000 010001 011110 111010 100001 100110 010100  100111

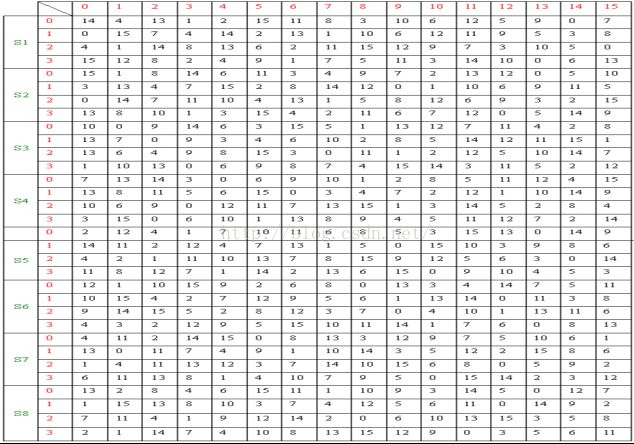
(2).将异或后的结果通过S盒子转换为32位

    将异或运算得到的48位结果数据分成8个6位的块，将每一块通过对应的一个S盒产生一个4位的输出，S盒接收6位的输入，经过置换输出4位的数据，具体置换过程为：

    将6位的输入中的第一位和第六位取出来1形成一个两位的二进制数X，将其转换为十进制作为行数，然后将中间4位构成另一个二进制数Y，并将其转换为十进制数作为列，然后查出S的X行Y列所对应的整数，将该整数置换为一个4位的二进制数，即S盒的输出。（eg：输入数据中的第一个6位数据块位010111，则需要通过查S1盒，先取出010111的第一位和第六位，则X=01，其对应的十进制为1。然后取出中间4位的1011，则Y = 1011，其对应的十进制为11，在S1盒中第1行11列的数为11，将其转换为二进制位1011，则输出1011）

 将第一步得到的结果： 011000 010001 011110 111010 100001 100110 010100  100111

进行S盒置换得到的十进制为：5 10 7 10 15 8 6 2

转换为相应的二进制位：0101 1010 0111 1010 1111 1000 0110 0010

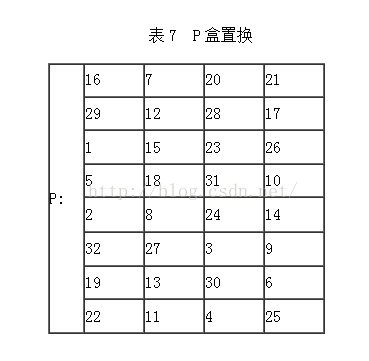
3.进行P盒置换

    将S盒输出结果再通过一个P盒置换产生一个32位输出

上步得到的结果使用P盒置换后得到的结果为：

                                     0111 0101 0101 1111 1000 0100 1100 0110

将此结果与 L0（32位） = 1100 1100 0000 0000 1100 1100 1111 1111

进行异或运算得到结果为：1011 1001 1010 0000 0100 1000 0011 1001

4.左右交换位置

将上步的结果赋给R1

    即R1 = 1011 1001 1010 0000 0100 1000 0011 1001

R0则原封不动的赋给L1

    即L1 =  R0（32位） = 1111 0000 1010 1010 1111 0000 1010 1010

之后进入下一轮迭代。最后生成L16和R16，其中R16为L15与P盒置换结果做异或运算的结果，L16是R15的直接赋值

5.密文的生成

    经过16次的迭代，我们得到了16对32位的数据块，即L1R1,L2R2,......L16R16;

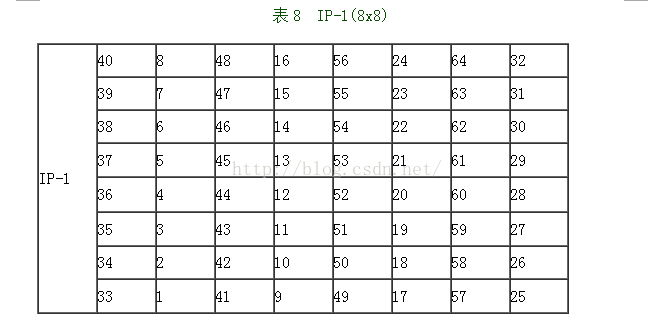
    最后一对L16R16就是我们需要的。然后将L16与R16的位置交换，继续对R16L16（64位）运用一次IP-1排列

即在：L16（32位） = 0100 0011 0100 0010 0011 0010 0011 0100

          R16（32位） = 0000 1010 0100 1100 1101 1001 1001 0101

     R16L16（64位） = 00001010 01001100 11011001 10010101 01000011  01000010 00110010 00110100

时，对R16L16运用IP-1，得

IP-1（64位） = 10000101 11101000 00010011 01010100 00001111 00001010 10110100 00000101

                    =85E813540F0AB405

至此，我们就得到了明文M的密文。

以上为加密过程，要解密，依次反向计算即可。

参考博客：https://blog.csdn.net/yxtxiaotian/article/details/52025653

                 http://www.doc88.com/p-9909383710144.html