从零开始学习使用神经网络的计算机视觉（一）

作者 | 李新阳

学校 | 厦门大学本科在读

方向 | 计算机视觉

预备知识：需要一定的矩阵以及微积分知识

一、系列描述

本次从零教程我本人也是边学边写，有混淆或错误的地方请您通过各种方式尽情指教，学习的思路主要参考李菲菲教授的公开课以及自己的一些思路整理，希望我能描述清楚。对于算法我都要求自己一定贴出自己写的源代码，数据集会采用公开但不一定完全的权威数据集，读者可以酌情尝试，我尽可能写出结构化且具有可视化功能的TensorFlow源码，也请大家多加指点。还有一点是，本系列的计算机视觉会较多地以神经网络和深度学习为架构的模型进行描述，关于传统的计算机视觉，我将会在自己有所了解后进行一些说明。

二、开始计算机视觉的起点：MNIST数据集+Softmax分类器

1. 前戏开始

MNIST应该是最简单，也是最好的起始数据集，使用极为简单的分类器就可以达到不错的泛化准确率（何为泛化？即我们的模型对于没有进入训练集的判断能力，反应了模型是否正确或是鲁棒），实际上，基本上由图像各密集像素区的简单分布就可以达到分类手写数字识别的目的（特别是限制了手写范围，数字一般处于居中的位置的时候）。

2. 直接上代码吧

下面是Softmax函数进行MNIST分类的代码：

# coding=utf-8
from tensorflow.examples.tutorials.mnist import input_data

import tensorflow as tf

mnist = input_data.read_data_sets("MNIST_data/", one_hot=True)  # 读取图片数据集

sess = tf.InteractiveSession()  # 创建session

# 输入是序列化后的图片向量，注意只有一个通道，对应输入的28*28向量

xs = tf.placeholder(tf.float32, [None, 28 * 28 * 1])

# 类别是0-9总共10个类别，对应输出分类结果

ys = tf.placeholder(tf.float32, [None, 10])

# 分别对应权值矩阵和偏置矩阵
W = tf.Variable(tf.zeros([784,10]))
b = tf.Variable(tf.zeros([10]))

# 输出y

y = tf.nn.softmax(tf.matmul(xs, W) + b)

# 定义交叉熵为loss函数

cross_entropy = -tf.reduce_sum(ys * tf.log(y))

# 设置梯度下降，步长为0.01，目标是最小化交叉熵

train_step = tf.train.GradientDescentOptimizer(0.01).minimize(cross_entropy)

# 给出正确率的计算公式

correct_prediction = tf.equal(tf.argmax(y, 1), tf.argmax(ys, 1))

accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

# TensorFlow变量初始化

tf.global_variables_initializer().run()

# 循环训练步骤

for i in range(2000):

    # 随机取一部分数据集作为训练集

    batch = mnist.train.next_batch(100)

    train_step.run(feed_dict={xs: batch[0], ys: batch[1]})

    if i % 10 == 0:
        train_accuracy = accuracy.eval(feed_dict={xs: batch[0], ys: batch[1]})
        print("step %d, training accuracy %g" % (i, train_accuracy))

# 输出最终的正确率

print("test accuracy %g" % accuracy.eval(feed_dict={xs: mnist.test.images, ys: mnist.test.labels}))

来自本人Github

---

！推荐大家在运行和阅读了程序后再进行下面的阅读

---

虽然这是一个极为简单的分类器，但已经达到了90%左右的准确率，其中已经有许多神经网络中经常使用的思想在里面了，大家在阅读代码之后一定有许多疑惑，我先解释一些我觉得比较重要的概念性问题。

3. 从头开始，让我解释一下

1）. 关于Softmax

我们先很简单地描述一下Softmax函数，它将一组向量变为了另一组向量，且另一组向量具有某种概率以及统计上的含义，更类似于对于结果的“标准化”，但以概率分布的形式给出，我给出的公式是以向量和函数的形式写出。

Softmax(x→)=exp(x→)sum(exp(x→)) S o f t m a x ( x → ) = e x p ( x → ) s u m ( e x p ( x → ) )

其中需要说明的是：exp()函数返回的是与输入量x行列一致的，sum()函数是将矩阵中的每一个元素加起来的总和，实际上，更专业的写法为：

Si=exi∑j(exj) S i = e x i ∑ j ( e x j )

含义与上面实际上是一致的，一个对向量整体进行运算，一个对元素进行运算。

2）. 关于交叉熵

一句话描述交叉熵：就是一个值，用来描述最终分类结果正确的可能性
公式如下：

L=−∑jy′j⋅log(yj) L = − ∑ j y j ′ ⋅ l o g ( y j )

其中， y′j y j ′ 表示该图片的第j个标签是否为正确的（实际上只有一个为1，其他均为0）， yj y j 表示我们预测的第j个为正确的输出值，也就是经过Softmax后的概率值，实际上，这里的 yj y j ，就是我们前面得到的 Si S i 。
至于为什么要采用交叉熵来作为损失值，我们先介绍一下梯度下降和链式法则。

3）. 关于梯度下降和链式法则

关于梯度下降，我觉得各位应该有些许了解，这里用的最简单的梯度下降，直接对于原本的一个参数 w w ，增或减一个步长0.05乘以他的下降率 ∂L∂w ∂ L ∂ w ，对于每一个 w w ，我们很难通过直接的算式推到来得到他的下降率，而是通过数值方法以及链式法则来进行反向传播。反向传播的概念我在这里不再赘述，实际上，梯度作为反向传播的最重要概念我想用一个更简单的办法来描述：

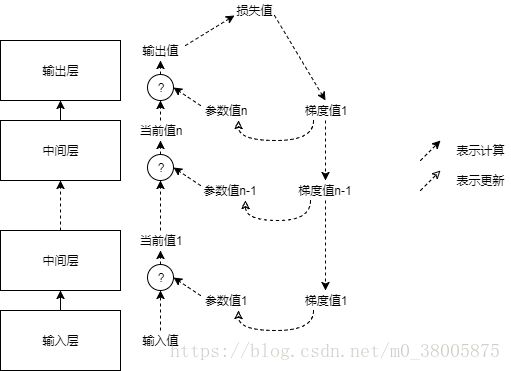
我们用一段话描述整个网络的训练过程，可以说成是输入作用到输出，输出与真实值的差异作用到参数，从而一步一步使输出与真实值的差异缩小，我们以上层为网络拓扑顺序靠后的层，从上图可以看到，每一层在进行正向传播时，都需要根据下层的值和参数值得到自己的当前值（如何得到取决于该层的固有运算），在最后一层得到输出值后，由真实值和输出值得到损失值，再有损失值倒推出各层的梯度值（求下层的梯度可能会需要上层的梯度以及更下层或自身的当前值，所以说要存储当前值），根据梯度值和步长更新参数值，然后进行下一次训练。
当然，实际上的过程涉及了大量的运算，包括链式法则以及雅可比矩阵等知识我在这里不详说，实际上，大多数已知的神经网络结构，都可以在TensorFlow上自动地进行正向传播和反向传播，之后我可能会设计一些不在库中的中间层，到时候会详细地进行讲解和推到。

4）. 网络干了什么

大家应该可以看出来，我们的网络实际上只有一层，那它到底干了什么？
实际上，我们可以很简单地理解到这一层在干什么，实际上对于每个输出，比如是不是0，网络会用权值和偏执向量的一部分作用于输入向量，然后得出是0的得分，事实上，这样的一个乘法，是否可以想成是权值图直接作用于输入图呢，有趣的事情发生了，我们将权值矩阵分成10条向量，再转成28*28的灰度图，看会发生什么（下面这张图的源代码我也会传在github上，使用了前面训练网络得到的权值矩阵，所以前面的训练过程后面加了几句话，大家也可以在源代码里看到）：

来自本人Github
其中，边缘的灰色部分表示权值为0，偏白的部分表示权值大于0，偏黑的部分表示权值小于0。
我们仔细地观察0的权值图，会发现，周围一圈是权值大于0的部分，当输入图在此区域有分布的话，则它为0的几率就会增加，但注意，圆的中心有一块区域权值小于0，也就是说，当输入图在此中心区域有分布的话，则它为0的几率就会减少，这对于我们来说有很直观的理解，读者可以按照此思路，观察其他数字的权值图。（这也是少有的我们可以完全理解的网络了。）

3. 总结一下

本文介绍了一个最简单的网络，可以较快地训练，完成不错的准确率，虽然实际上都还不算是神经网络，但其中对于损失函数，梯度下降等概念已经形成，下一次将讲解CNN，卷积神经网络，内容会稍微复杂一点，希望大家可以充分理解这一篇的内容再看下一篇（还没有写好，我尽量在18年7月11日前写出）。