ACE：Aggregation Cross-Entropy for Sequence Recognition（聚合交叉熵） ---- 论文阅读笔记

聚合交叉熵（Agregation Cross-Entropy，ACE）

论文链接：https://arxiv.org/abs/1904.08364

论文翻译：https://blog.csdn.net/m0_38007695/article/details/96876075

CTC和注意力机制问题：

1. 前向后向算法实现复杂，导致大量的计算消耗；
2. 很难应用与2D预测问题；
3. 注意机制依赖于其注意模块来进行标签对齐，导致额外的存储需求和计算消耗。

为了解决上述的问题，该论文提出了聚合交叉熵损失函数（ACE）：

首先，ACE不是通过最大化每个位置处的预测概率来最小化损失函数，而是通过不考虑序列之间的顺序，只关心每个类的累计概率来简化问题，只要求网络精确预测每一类的字符数来最小化损失函数。其次，ACE可以解决2D预测问题。

---

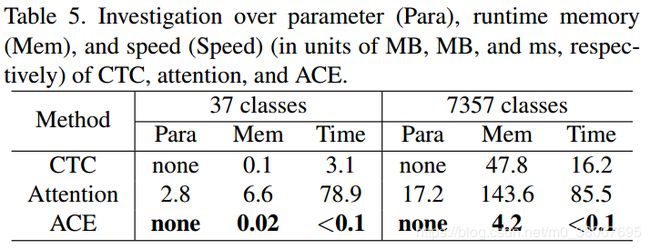
CTC、Attention和ACE比较：

复杂性分析

   ACE损失函数的总体计算是基于四个基本公式实现的，分别有 $O(1),O(|C^{ϵ}|),O(|C^{ϵ}|),O(|C^{ϵ}|)$ 的计算复杂度。因此，ACE损失函数的计算复杂度是 $O(|C^{ϵ}|)$ 。这四个公式中的逐元素乘法，除法和 log 操作可以在 GPU 以 $O(1)$ 复杂度并行实现。相反，基于前向后向算法的CTC的实现有一个 $O(T\ast |S|)$ 的复杂度。因为CTC的前向变量和后向变量 依赖于之前的结果计算当前的输出，所以CTC很难在时间维度上并行加速。CTC的基本操作也非常复杂的，导致总体消耗时间大于ACE。关于注意力机制，其计算复杂度与“注意力”的时间成比例。每次注意模块的计算复杂度已经具有与CTC相似的量级。

  从内存消耗的角度来看，提出的ACE损失函数几乎不需要内存消耗，因为可以根据四个基本公式直接计算ACE损失结果。 但是，CTC需要额外的空间来保存与时间步长 $T$ 和序列标注长度成比例的前向后向变量。同时，注意机制需要额外的模块来实现“注意力”。 因此，其内存消耗量明显大于CTC和ACE。

  总的来看，与CTC和注意力比较，提出的ACE损失函数在计算复杂性和内存需求方面都表现出显着的优势。

  论文中将ACE的参数，运行时内存和运行时间与CTC和注意力的参数，运行时内存和运行时间进行比较。在12GB内存的单个NVIDIA TITAN X图形卡上使用minibatch 64和模型预测长度T = 144执行结果。ACE运行时需要的内存比CTC和注意力少五倍，速度至少是CTC和注意力的30倍。

ACE优点：

1. 时间复杂度和空间复杂度低。由于只需要四个基本公式，所以可以更快，需要更少的内存；
2. 可以应用于识别常规、不规则文本和手写文本；
3. 可以适应2D预测问题，将2D预测平坦化为1D预测；
4. 不需要关心实例顺序问题，可以应用于计数问题。

ACE实现步骤（四个基本公式）：

给定模型预测 $y_k^t$ 和它的标注 $N$，基于交叉熵的 $\mathrm{A}\mathrm{C}\mathrm{E}$ 损失函数的实现有如下步骤：

1. 沿时间维度聚合每个类别的概率

   $y_k={\sum }_{t=1}^T{y}_k^t$ 通过对全部时间的第 $k$ 类的概率求和，计算每一个类的字符数量；

2. 将累积结果和标签标注标准化为所有类别的概率分布

   ${\overline{y}}_k=y_k/T$ 标准化累加的概率，${\overline{N}}_k=N_k/T$ 标准化标注；

3. 使用交叉熵比较这两个概率分布

   $L(I,S)=-{\sum }_{k=1}^{|C^{ϵ}|}{\overline{N}}_k\ln {\overline{y}}_k$ 估计在 ${\overline{N}}_k$ 和 ${\overline{y}}_k$ 之间的交叉熵

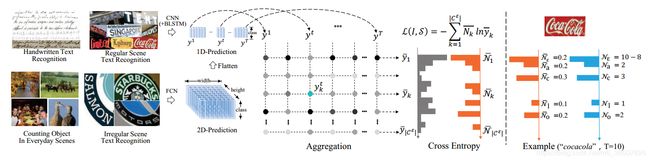
   模型预测 $y_k^t$ 通常是通过集成的 CNN-LSTM模型（1D预测）或者FCN模型（展平的2D预测）提供的。所以，ACE的输入与CTC的输入相同。因此，提出的ACE可以很方便的通过代替框架中的CTC层来应用。

$\{y_k^t,t=1,2,\cdots ,T,k=1,2,\cdots ,|C^{\epsilon }|\}$ ，其中 $C^{\epsilon }=C\cup \epsilon$ ，$C$ 是字符集合，$\epsilon$ 是空格。

（左）通常，1D和2D预测分别由集成的CNN-LSTM和FCN模型生成。 对于ACE损失函数，2D预测进一步展平为1D预测 $\{y_k^t,t=1,2,\cdots ,T\}$ 。在聚合期间，所有时间点的1D预测都是为每个类独立累积的，根据 $y_k={\sum }_{t=1}^T{y}_k^t$ 。在归一化之后，将预测 $\overline{y}$ 与GroundTruth $\overline{N}$ 一起用于基于交叉熵的损失估计。（右）一个简单的例子表明ACE损失函数的标签的生成。$N_a=2$ 表明在 cocacola中有两个 “a”。

---