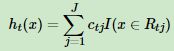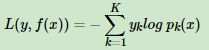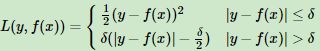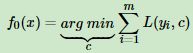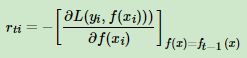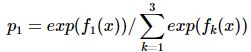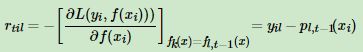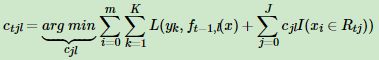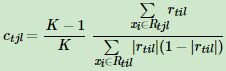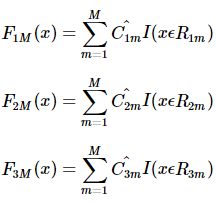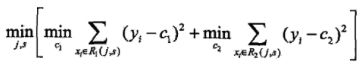【算法梳理Task2】GBDT算法梳理

1.GBDT思想

GBDT是集成学习Boosting家族的成员。弱学习器限定了只能使用CART回归树模型，迭代是思路是：在本轮迭代中找到一个CART回归树模型的弱学习器使得本轮的损失函数最小。即拟合误差。（Adaboost是利用前一轮迭代弱学习器的误差率来更新训练集的权重，这样一轮轮的迭代下去。）

GBDT的思想使其具有天然优势可以发现多种有区分性的特征以及特征组合。

• 回归树（Regression Decision Tree）

回归树生成算法：（CART）

• 提升树（Boosting Decision Tree）

提升方法采用加法模型和前向分布算法。以决策树为基函数的提升方法称为提升树。

提升树是迭代多棵回归树来共同决策。当采用平方误差损失函数时，每一棵回归树学习的是之前所有树的结论和残差，拟合得到一个当前的残差回归树，残差的意义如公式：残差 = 真实值 - 预测值 。提升树即是整个迭代过程生成的回归树的累加。

回归问题的提升树算法流程：

• 梯度提升决策树

对于一般的损失函数，往往每一步优化没那么容易，如绝对值损失函数和Huber损失函数。针对这一问题，Freidman提出了梯度提升算法：利用最速下降的近似方法，即利用损失函数的负梯度在当前模型的值，作为回归问题中提升树算法的残差的近似值，拟合一个回归树。

算法流程：

2.负梯度拟合

针对各种各样损失函数如何让进行通用性拟合的问题，Freidman提出了用损失函数的负梯度来拟合本轮损失的近似值，进而拟合一个CART回归树。

第t轮的第i个样本的损失函数的负梯度表示为：

拟合得到CART回归树后，针对每一个叶子节点里的样本，我们求出使损失函数最小，也就是拟合叶子节点最好的的输出值ctjctj如下：

得到本轮的决策树拟合函数：

从而得到本轮的强学习器如下：

3.损失函数

• 对于分类算法

• 指数损失函数

• 对数损失函数

（二分类）

（多分类）

• 对于回归算法

• 均方差

• 绝对损失

，对应负梯度：

• Huber损失（均方差和绝对损失的折中产物，对于远离中心的异常点，采用绝对损失，而中心附近的点采用均方差。这个界限一般用分位数点度量）

，对应负梯度：

• 分位数损失（回归前指定为分位数）

对应负梯度：

4.回归分类

• 回归算法

输入：训练集样本T，最大迭代次数T, 损失函数L。

输出：强学习器

【流程】

• 初始化弱学习器：

• 迭代论数 t = 1,...T
  • m个样本的负梯度：

  • 

  • 根据样本残差（负梯度）拟合一颗CART回归树。
  • 叶节点区域（j个）的最佳拟合值

  • 

  • 更新学习器：

  • 

• 得到强学习器：

• 分类算法（二元）

• 首先明确一点，gbdt 无论用于分类还是回归一直都是使用的CART 回归树。
• 核心是因为gbdt 每轮的训练是在上一轮的训练的残差基础之上进行训练的。这里的残差就是当前模型的负梯度值 。这个要求每轮迭代的时候，弱分类器的输出的结果相减是有意义的。残差相减是有意义的。

• 损失函数选：

• 标签为{-1,1},负梯度误差为：

• 各个叶子节点的最佳残差拟合值为：

• 使用近似值代替：

5.多元分类

算法流程：

• 损失函数：

• 在训练的时候，是针对样本 X 每个可能的类都训练一个分类回归树。

     【将类别转为向量表示。假设共3类，样本x属于第二类，则类别记为[0，1，0]】

• 每颗树的训练过程其实就是就是我们之前已经提到过的CATR TREE 的生成过程。之后得到多棵树对于样本x的预测值
• 仿照多分类的逻辑回归 ，使用softmax 来产生概率，则属于类别 1 的概率：

（使用对数似然损失函数）

• 更新残差：

      （推出负梯度误差）

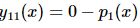
                                     （对于一个属于第二类的样本）

• 各个叶子节点的最佳残差拟合值为：（K是类别数）

       

      上述式子较难优化，选择近似值替代：

      

• 构造的分类器：

                              

6.正则化

• 和Adaboost类似的正则化项，即步长(learning rate)。定义为ν。（Shrinkage 的思想）

 加入正则化后变为：

 

 ν的取值范围为0<ν≤1。对于同样的训练集学习效果，较小的ν意味着我们需要更多的弱学习器的迭代次数。通常我们用步长和迭代最大次数一起来决定算法的拟合效果。

• 通过子采样比例（subsample）。取值为(0,1]。

这里是不放回抽样。如果取值为1，则全部样本都使用，等于没有使用子采样。如果取值小于1，则只有一部分样本会去做GBDT的决策树拟合。选择小于1的比例可以减少方差，即防止过拟合，但是会增加样本拟合的偏差，因此取值不能太低。推荐在[0.5, 0.8]之间。

使用了子采样的GBDT有时也称作随机梯度提升树(Stochastic Gradient Boosting Tree, SGBT)。减少弱学习器难以并行学习的弱点。

• 对于弱学习器即CART回归树进行正则化剪枝。

7.优缺点

• 优点

• 可以灵活处理各种类型的数据，包括连续值和离散值。

• 在相对少的调参时间情况下，预测的准确率也可以比较高。这个是相对SVM来说的。

• 使用一些健壮的损失函数，对异常值的鲁棒性非常强。比如 Huber损失函数和Quantile损失函数。

• 缺点

• 由于弱学习器之间存在依赖关系，难以并行训练数据。（SGBT进行了改善）

8.sklearn参数

Boosting框架的重要参数：

• loss  {‘deviance’, ‘exponential’}, 默认‘deviance’

损失函数。有对数似然损失函数"deviance"和指数损失函数"exponential"两个选项。一般来说，推荐使用默认的对数似然损失函数"deviance"，它对于二元分类和多元分类都有较好的优化效果。而指数损失函数"exponential"相当于执行了Adaboost算法。

• learning_rate   float，范围（0，1]，默认0.1

弱学习器的权重缩减系数ν。

• n_estimators  int (default=100)

弱学习器的最大迭代次数，或者说最大的弱学习器个数。一般来说n_estimators太小，容易欠拟合，而n_estimators太大，又容易过拟合。调参过程中，常常将它和参数learning_rate一起来考虑。

• subsample   float,  (default=1.0)

子采样比例，取值为(0,1]。推荐在[0.5, 0.8]之间选择。

• init  estimator

初始化的弱学习器。。如果不输入，则用训练集样本来做样本集的初始化分类回归预测，否则使用init参数提供的学习器来做初始化分类回归预测。一般用在我们对数据有先验知识或者之前做过拟合的时候，否则就不用考虑这个参数了。

 

• validation_fraction   float （0，1），默认0.1

验证集比例。在n_iter_no_change为integer时使用，用于提前终止训练。

• n_iter_no_change  int, default None

None表示不会提前终止训练。为int时表示验证集的评分在多轮迭代中没有提高，则停止训练。

• tol    float, optional, default 1e-4

提前停止的容忍程度。在n_iter_no_change轮迭代中，损失都没能提高tol，则停止训练。

决策树类相关参数：

决策树相关参数。在随机森林算法中已经对这些参数进行了细致的说明：

https://blog.csdn.net/m0_38019841/article/details/85100588

• criterion 
• max_depth 
• max_features 
• min_samples_split 
• min_samples_leaf 
• min_weight_fraction_leaf 
• min_impurity_decrease 
• min_impurity_split 
• max_leaf_nodes 
• random_state
• verbose
• warm_start 
• presort   bool, optional (default=False)

是否预先对数据排序以加快拟合中最佳分裂的发现。

9.应用场景

• Facebook使用其来自动发现有效的特征、特征组合，来作为LR模型中的特征，以提高 CTR预估（Click-Through Rate Prediction）的准确性
• GBDT在淘宝的搜索及预测业务上也发挥了重要作用

10.几个问题

• gbdt如何选择特征

CART TREE 生成的过程其实就是一个选择特征的过程。

在每轮迭代的时候，如何选择这个特征 j,以及如何选择特征 j 的切分点 m？

【答】们先遍历训练样本的所有的特征，对于特征 j，我们遍历特征 j 所有特征值的切分点 c。找到可以让下面这个式子最小的特征 j 以及切分点c.

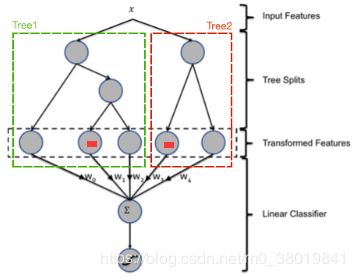
• gbdt 如何构建特征

根据样本落在多棵决策树叶子节点的情况，重新得到特特征向量。

如上图，得到向量[0，1，0，1，0]作为样本x的组合特征，输入到后续模型中。

• gbdt在调参时为什么树的深度很少就能达到很高的精度？用随机森林需要把树的深度调的很高才可以？

Boosting主要关注降低偏差；Bagging主要关注降低方差。

对于Boosting来说，每一步我们都会在上一轮的基础上更加拟合原数据，所以可以保证偏差（bias）,所以对于每个基分类器来说，问题就在于如何选择variance更小的分类器，即更简单的分类器，所以我们选择了深度很浅的决策树。

对于Bagging算法来说，由于我们会并行地训练很多不同的分类器的目的就是降低这个方差(variance) ,因为采用了相互独立的基分类器多了以后，预测值自然就会靠近.所以对于每个基分类器来说，目标就是如何降低这个偏差（bias),所以我们会采用深度很深甚至不剪枝的决策树。

参考：

https://www.cnblogs.com/pinard/p/6140514.html

https://www.cnblogs.com/ModifyRong/p/7744987.html

https://www.jianshu.com/p/005a4e6ac775