树链剖分笔记

树链剖分笔记

• By BigYellowDog
• 前置芝士：dfs序、线段树、LCA思想

前言

• 为什么要学？其实树剖是一种高级的数据结构了。一般来说，省选以上才会用到。但是，往往一些题需要巧妙的利用现有知识（如LCA、树上差分啥的），但是巧妙往往很难想到。这个时候，用一些高级的数据结构直接暴力去解就可以A了。换句话说，智商不够，数据结构来凑。
• 树剖是什么？假设现在要你将树上的一条链加上一个权值，怎么办？显然可以树上差分。那要你查询树上的一条链之和，怎么办？显然可以LCA。那么，如果我把上述两个问题结合起来呢？也就是在线修改，在线查询。这时用差分和LCA就很难做了。于是，可以用一个功能强大的数据结构统一统统解决。

Dfs序

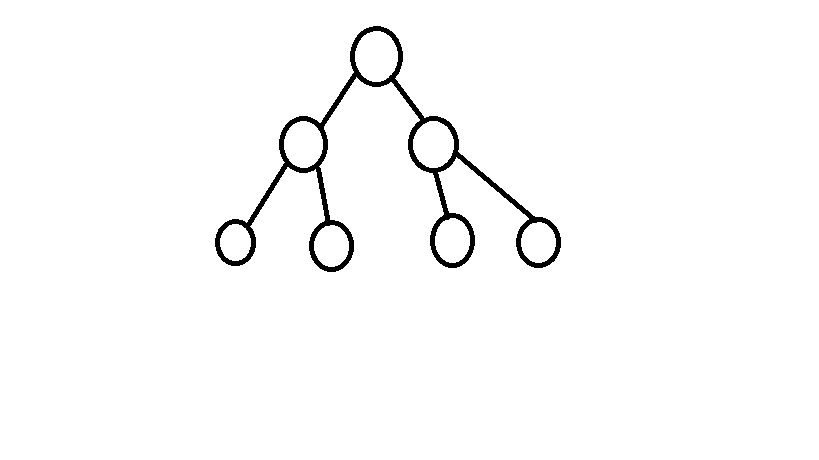
• 首先来看这么一幅图（一棵树）：

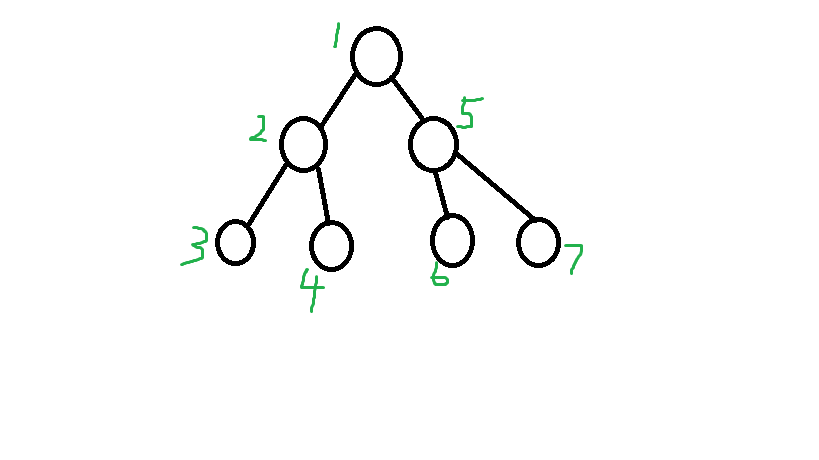
• 将这颗树标上Dfs序，得到如下：

• 发现什么规律？显然以任意一个节点为根时，这颗子树的Dfs序是连续的。
• 那么一棵树通过Dfs序就被弄成了一个区间。
• 好，那现在假如要让你将以x为根的子树统统加上一个数，怎么办？
• 开个线段树啊。那么只需要在[dfn[x], dfn[x] + size[x] - 1]这一段区间上修改即可。（dfn[x]为x的dfs序）。问题解决。
• 但是，如果让你将一条链统统加上一个数怎么办a？可以发现，一条链上的点的Dfs序不一定是连续的。那么就无法在线段树上进行区间修改了。
• 为了解决这个问题，树剖的核心思想——剖，就发挥作用了。

树链剖分

• 剖，字面意思，就是将树剖成一条一条的链。使得查询的链的Dfs是“连续”的，从而使用线段树处理。连续打引号是因为一条链被拆成了很多段，每一段链的Dfs是连续的。
• 剖可以有很多种剖法，这里介绍最常用的重链剖分。
• 为此，了解一下又chou又长的概念：

1. 重儿子：父亲节点的所有儿子中子树结点数目最多（size最大）的结点；
2. 轻儿子：父亲节点中除了重儿子以外的儿子；
3. 重边：父亲结点和重儿子连成的边；
4. 轻边：父亲节点和轻儿子连成的边；
5. 重链：由多条重边连接而成的路径；
6. 轻链：由多条轻边连接而成的路径；

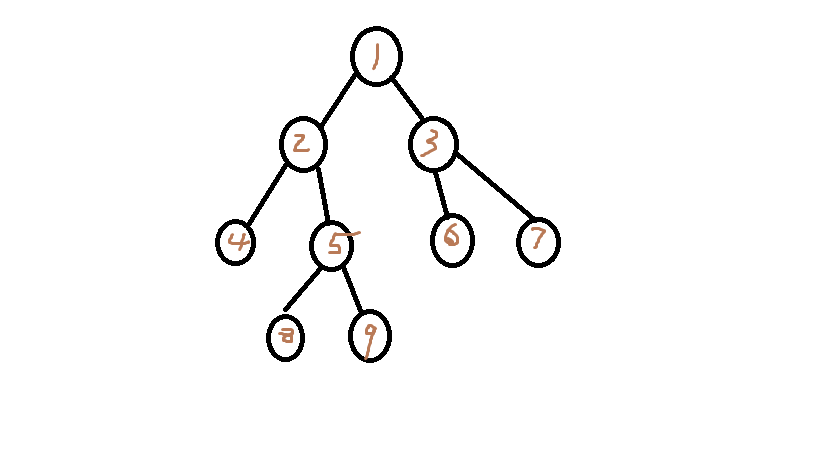
• 看个图吧：

• 1的重儿子是2或3。因为2、3的子树大小一样，随便选一个。
• 2的重儿子是5，因为5子树大小 > 4子树大小。
• 1 -> 2是一条重边，2 -> 5是一条重边。
• 1 -> 2 -> 5是一条重链。
• OK，那么知道了概念，如果算出这些量呢？
• Dfs呗。

• 看看我们需要解决哪些量：size（子树大小）、son（重儿子）、fat（父亲）、dep（深度）（其实只要算这些=.=）。算size和fat和dep你们都会，算son无非比较一下儿子的size就好。

• 算出这些量又怎么样呢！！？？
• e... ...别急。
• 我们的目的是将树剖成一条条重链。但是，目前为止，还没有剖啊。

• 所以，还需要算出top[x]（x所在重链的头）和dfn[x]（Dfs序(重链规则下的Dfs序)）

• 算出这两个量还要来一次Dfs，文字语言解释很费力，我们来看代码：

void dfs(int x, int head)
{
    top[x] = head, dfn[x] = dex;
    if(!son[x]) return;
    dfs(son[x], head);
    for(int i = h[x]; i != 0; i = e[i].next)
        if(e[i].to != fat[x] && e[i].to != son[x])
            dfs(e[i].to, e[i].to);
    //应该没打错，现场手敲的QAQ
}

• 传两个参，x当前节点，head当前节点所在重链的头。
• 每次碰到一个点x，先将它的top = head。非常容易。给它标上Dfs序，注意，这里的Dfs序是按剖分的顺寻规定的。
• 然后如果它没有重儿子，说明x是叶子节点了。直接return。
• 否则说明它有重儿子，那么它的重儿子跟它一定是在一条重链上的。那么传下去。

• 安排好它的重儿子后，它的轻儿子显然不跟它在同一条链上，那么它的轻儿子只能自立门户，作为一条新链的头。

• 好，通过第一次Dfs算出size、son、fat、dep，第二次Dfs算出top、dfn后。我们上面的图就可以被五马分尸成这个样子：

• 1 -> 2 -> 5 -> 8是一条链；3 -> 7是一条链；6是一条链；9是一条链；4是一条链。
• 天蓝色数字为重链剖分规则下的Dfs序。
• 假如让你将8号节点到7号节点的链上加上一个数，怎么办？
• 这样做：
• 因为：8号节点的头 != 7号节点的头，说明它们不在同一条链上，需要向上跳
• 因为：8号节点深度 > 7号节点深度，所以8号往上跳。
• 所以：8号节点跳到它的头——1号点，同时在线段树上修改区间[2, 4]。然后再跳到1的爸爸0号点。
• 因为：0号节点深度 < 7号节点深度，所以7号往上跳。
• 所以：7号节点跳到它的头——3号点，同时在线段树上修改区间[7, 8]。然后再跳到3的爸爸1号点。
• 因为0号的头 = 1号的头 = 0，所以结束。
• 看看，我们将所要操作的链分成了几条重链，然后在线段树上操作。搞定，查询的话同理。
• 现在知道为什么Dfs序要按照重链剖分的规则下定义了吧，因为要保证同一条重链中Dfs序是连续的。

代码实现

• 上面一大坨就是原理的理解。
• 那么我们来看看模板题如何写：
• 洛谷树剖模板题面

//从主函数开始阅读
#include 
#include 
#define N 100005
using namespace std;

struct T {int l, r, val, tag;} t[N * 4];
struct E {int next, to;} e[N * 2];
int n, m, root, mod, num, tot;
int a[N], h[N], fat[N], dep[N], size[N];
int son[N], top[N], dfn[N], val[N];

int read()
{
    int x = 0; char c = getchar();
    while(c < '0' || c > '9') c = getchar();
    while(c >= '0' && c <= '9') {x = x * 10 + c - '0'; c = getchar();}
    return x;
}

void add(int u, int v)
{
    e[++num].next = h[u];
    e[num].to = v;
    h[u] = num;
}

void dfs1(int x, int fath, int depth)
{
    fat[x] = fath, dep[x] = depth, size[x] = 1; //正常操作
    int maxSon = 0;
    for(int i = h[x]; i != 0 ; i = e[i].next)
        if(e[i].to != fath)
        {
            dfs1(e[i].to, x, depth + 1);
            size[x] += size[e[i].to];
            if(size[e[i].to] > maxSon) //比较儿子的子树大小找出重儿子
            {
                maxSon = size[e[i].to];
                son[x] = e[i].to;
            }
        }
}

void dfs2(int x, int head)
{
    top[x] = head, dfn[x] = ++tot, val[tot] = a[x];
    //这里多出来个val数组之前没提到的，是拿来记录每个dfn序所表示的值。
    //拿来线段树建树用的。
    if(!son[x]) return;
    dfs2(son[x], head);
    for(int i = h[x]; i != 0; i = e[i].next)
        if(e[i].to != son[x] && e[i].to != fat[x])
            dfs2(e[i].to, e[i].to);
}

void build(int p, int l, int r)
{
    t[p].l = l, t[p].r = r;
    if(l == r) {t[p].val = val[l]; return;}
    int mid = (l + r) >> 1;
    build(p << 1, l, mid), build(p << 1 | 1, mid + 1, r);
    t[p].val = t[p << 1].val + t[p << 1 | 1].val;
    t[p].val %= mod;
}

void down(int p)
{
    int son1 = p << 1, son2 = p << 1 | 1;
    t[son1].tag += t[p].tag, t[son2].tag += t[p].tag;
    t[son1].tag %= mod, t[son2].tag %= mod;
    t[son1].val += (t[son1].r - t[son1].l + 1) * t[p].tag;
    t[son2].val += (t[son2].r - t[son2].l + 1) * t[p].tag;
    t[son1].val %= mod, t[son2].val %= mod;
    t[p].tag = 0;
}

void upd(int p, int l, int r, int add)
{
    if(t[p].l >= l && t[p].r <= r)
    {
        t[p].tag += add, t[p].tag %= mod;
        t[p].val += (t[p].r - t[p].l + 1) * add;
        t[p].val %= mod;
        return;
    }
    if(t[p].tag) down(p);
    int mid = (t[p].l + t[p].r) >> 1;
    if(l <= mid) upd(p << 1, l, r, add);
    if(r > mid) upd(p << 1 | 1, l, r, add);
    t[p].val = t[p << 1].val + t[p << 1 | 1].val;
    t[p].val %= mod;
}

int ask(int p, int l, int r)
{
    if(t[p].l >= l && t[p].r <= r) return t[p].val % mod;
    if(t[p].tag) down(p);
    int mid = (t[p].l + t[p].r) >> 1, ans = 0;
    if(l <= mid) ans += ask(p << 1, l, r), ans %= mod;
    if(r > mid) ans += ask(p << 1 | 1, l, r), ans %= mod;
    return ans;
}

void updLink(int x, int y, int add)
{
    while(top[x] != top[y]) //如果头不一样，说明还没跳到同一条链上
    {
        if(dep[top[x]] < dep[top[y]]) swap(x, y); //让深度大的往上跳
        upd(1, dfn[top[x]], dfn[x], add); //更新这一段链
        x = fat[top[x]]; 
        //因为这一段链更新完了，所以没必要停留在头这，再往上跳一个
    }
    //执行到这里时，x和y已经是同一条链上的点了。
    //那么只需更新x -> y这一条值值的链就OK了。
    if(dep[x] > dep[y]) swap(x, y);
    upd(1, dfn[x], dfn[y], add);
}

int askLink(int x, int y) //原理跟updLink一模一样=.=
{
    int ans = 0;
    while(top[x] != top[y])
    {
        if(dep[top[x]] < dep[top[y]]) swap(x, y);
        ans += ask(1, dfn[top[x]], dfn[x]), ans %= mod;
        x = fat[top[x]];
    }
    if(dep[x] > dep[y]) swap(x, y);
    ans += ask(1, dfn[x], dfn[y]);
    return ans % mod;
}

int main()
{
    cin >> n >> m >> root >> mod;
    for(int i = 1; i <= n; i++) a[i] = read() % mod;
    for(int i = 1; i < n; i++)
    {
        int u = read(), v = read();
        add(u, v), add(v, u);
    }
    dfs1(root, 0, 1); //第一次dfs算出size、fat、dep、son
    dfs2(root, root); //第二次dfs算出dfn、top
    build(1, 1, n); //建树
    for(int i = 1; i <= m; i++)
    {
        int op = read();
        if(op == 1)
        {
            int x = read(), y = read(), add = read() % mod;
            updLink(x, y, add); //修改一条链
        }
        else if(op == 2)
        {
            int x = read(), y = read();
            printf("%d\n", askLink(x, y)); //查询一条链
        }
        else if(op == 3)
        {
            int x = read(), add = read() % mod;
            upd(1, dfn[x], dfn[x] + size[x] - 1, add);
            //虽然dfn是在重链剖分的规则下定义的，但是任满足一个子树的dfs序是连续的。
            //所以按照最开始讲的在线段树上修改即可。
        }
        else if(op == 4)
        {
            int x = read();
            printf("%d\n", ask(1, dfn[x], dfn[x] + size[x] - 1));
        }
    }
    return 0;
}

后言

• 来来来看一个好康的！松鼠找Sugar

• 这题标算LCA，但是直接暴力跑树剖是行了啊！题解转这里

• 数据结构吼a... ...

• 第一次敲学习笔记，挺累的。希对各位有所帮助吧OxO