Java高频算法--排序、查找总结

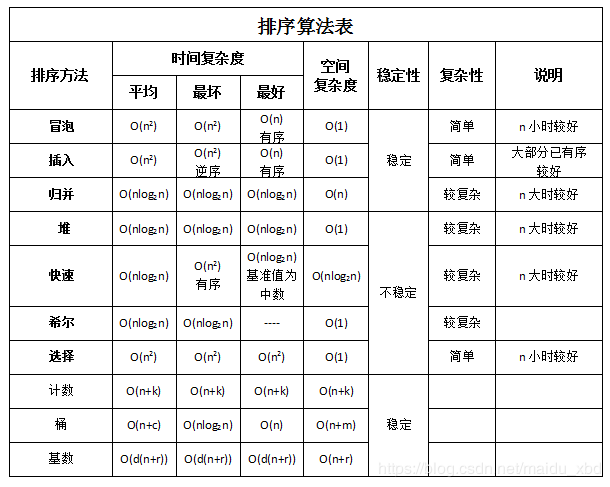
排序

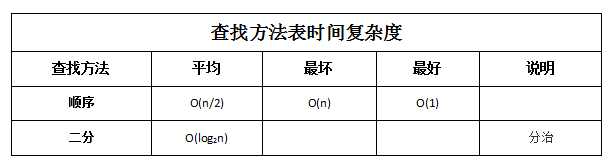
查找

冒泡排序

对于给定的n个记录，从最后一个记录开始依次对相邻的两个记录进行比较，当后面的记录小于前面的记录时，交换位置，进行一轮比较和换位后，n个记录中最小记录将位于第1位；然后对后（n-1）个记录进行第二轮比较；重复该过程直到进行比较的记录只剩下一个为止。

public class Solution1 {
	//冒泡排序
	public static void BubbleSort(int array[]) {
		int len=array.length;
		if(array==null||len<=0)
			return;
		for(int i=0;ii;j--)    //从后往前
				if(array[j]

快速排序

是一种非常高效的排序算法，“分而治之”。它的基本思想是：通过一趟排序将要排序的数据分割成独立的两部分，其中一部分的所有数据都比另外一部分的所有数据都要小，然后再按此方法对这两部分数据分别进行快速排序，整个排序过程可以递归进行，以此达到整个数据变成有序序列。一趟快速排序的算法是：

1）设置两个变量i、j，排序开始的时候：i=0，j=N-1；

2）以第一个数组元素作为关键数据，赋值给key，即key=A[0]；

3）从j开始向前搜索，即由后开始向前搜索(j--)，找到第一个小于key的值A[j]，将A[j]和A[i]互换；

4）从i开始向后搜索，即由前开始向后搜索(i++)，找到第一个大于key的A[i]，将A[i]和A[j]互换；

5）重复第3、4步，直到i=j； (3,4步中，没找到符合条件的值，即3中A[j]不小于key,4中A[i]不大于key的时候改变j、i的值，使得j=j-1，i=i+1，直至找到为止。找到符合条件的值，进行交换的时候i， j指针位置不变。另外，i==j这一过程一定正好是i+或j-完成的时候，此时令循环结束）

public class Solution2 {
	//快速排序
	  public static void QuickSort(int array[]){
		  Sort(array,0,array.length-1);
	  }
	  public static void Sort(int a[],int low,int high){
		  int i,j;
		  if (low>=high)return;
		  int index;
		  i=low;
		  j=high;
		  index=a[i];
		  while(i=index)
				  j--;
			  if(i

堆排序

是选择排序的一种。可以利用数组的特点快速定位指定索引的元素。堆分为大顶堆和小顶堆，是完全二叉树。对于给定的n个记录，初始时把这些记录看作一棵顺序存储的二叉树，然后将其调整为一个大顶堆，然后将堆的最后一个元素与堆顶元素交换，堆的最后一个元素即为最大记录；接着将前（n-1）个元素（即不包括最大记录）重新调整为一个大顶堆，再将堆顶元素与当前堆的最后一个元素进行交换得到次大的记录；重复该过程直至调整的堆中只剩下一个元素时为止，该记录即为最小记录，此时可得到一个有序序列。

public class Solution3 {
	//堆排序
  public static void adjustMinHeap(int a[],int pos,int len){
	  int temp;
	  int child;
	  for(temp=a[pos];2*pos+1<=len;pos=child){
		  child=2*pos+1;
		  if(childa[child+1]) 
			  child++;
		  if(a[child]=0;i--)
		  adjustMinHeap(array,i,len-1);
	  for(i=len-1;i>=0;i--){
		  int tmp=array[0];
		  array[0]=array[i];
		  array[i]=tmp;
		  adjustMinHeap(array,0,i-1);
	  }
  }
  public static void main(String[] args){
	  int a[]={3,9,8,4,2,1};
	  myMinHeapSort(a);
	  for(int i=0;i

插入排序

对于给定的一组记录，初始时假设第一个记录自成一个有序序列，其余记录为无序序列。接着从第二个记录开始，按照记录的大小依次将当前处理的记录插入到其之前的有序序列中，直至最后一个记录插入到有序序列中为止。

public class Solution4 {
	//插入排序
  public static void insertSort(int a[]){
	  if(a!=null){
		  for(int i=1;itemp){   //a[j-1]为前面排序好部分的最后一个元素。
				  while(j>=1&&a[j-1]>temp){
					  a[j]=a[j-1];
					  j--;
				  }
			  }
			  a[j]=temp;
		  }
	  }
  }
  public static void main(String[] args){
	  int a[]={3,9,8,4,2,1};
	  insertSort(a);
	  for(int i=0;i

选择排序

对于给定的一组记录，经过第一轮比较后得到最小的记录，然后将该记录与第一个记录的位置进行交换；接着对不包括第一个记录的其他记录进行第二轮比较，得到最小的记录并与第二个位置交换；重复该过程，直到进行比较的记录只有一个时为止。

public class SelectSort {
  public static void selectSort(int [] a){
	  int i,j;
	  int temp=0;
	  int flag=0;
	  int len=a.length;
	  for(i=0;i

希尔排序

是插入排序的一种。也称缩小增量排序，是直接插入排序算法的一种更高效的改进版本。希尔排序是把记录按下标的一定增量分组，对每组使用直接插入排序算法排序；随着增量逐渐减少，每组包含的关键词越来越多，当增量减至1时，整个文件恰被分成一组，算法便终止。先取一个小于n的整数d1作为第一个增量，把文件的全部记录分组。所有距离为d1的倍数的记录放在同一个组中。先在各组内进行直接插入排序；然后，取第二个增量d2

public class Shell {
  public static void ShellSort(int array[]){
	  int len=array.length;
	  int i,j;
	  int h;
	  int temp;
	  for(h=len/2;h>0;h=h/2){
		  for(i=h;i=0;j-=h){
				  if(temp

归并排序

利用递归和分治技术。对于给定的n个记录，首先将每两个相邻的长度为1的子序列进行归并，得到n/2（向上取整）个长度为2或1的有序子序列，再将其两两归并，反复执行此过程，直到得到一个有序序列。

import java.util.Arrays;
public class MergeSort {
	 public static void merge(int[] a, int low, int mid, int high) {
	        int[] temp = new int[high - low + 1];
	        int i = low;        // 左指针
	        int j = mid + 1;    // 右指针
	        int k = 0;
	        // 把较小的数先移到新数组中
	        while (i <= mid && j <= high) {
	            if (a[i] < a[j]) {
	                temp[k++] = a[i++];
	            } else {
	                temp[k++] = a[j++];
	            }
	        }
	        // 把左边剩余的数移入数组
	        while (i <= mid) {
	            temp[k++] = a[i++];
	        }
	        // 把右边边剩余的数移入数组
	        while (j <= high) {
	            temp[k++] = a[j++];
	        }
	        // 把新数组中的数覆盖nums数组
	        for (int k2 = 0; k2 < temp.length; k2++) {
	            a[k2 + low] = temp[k2];
	        }
	    }

	    public static void mergeSort(int[] a, int low, int high) {
	        int mid = (low + high) / 2;
	        if (low < high) { 
	            mergeSort(a, low, mid); // 左边 
	            mergeSort(a, mid + 1, high);  // 右边
	            merge(a, low, mid, high);  // 左右归并
	        }
	    }
	    public static void main(String[] args) {
	        int a[] = { 51, 46, 20, 18, 65, 97, 82, 30, 77, 50 };
	        mergeSort(a, 0, a.length - 1);
	        System.out.println("排序结果：" + Arrays.toString(a));
	    }
}

二分查找

又称折半查找，优点是比较次数少，查找速度快，平均性能好；其缺点是要求待查表为有序表，且插入删除困难。因此，折半查找方法适用于不经常变动而查找频繁的有序列表。二分查找的基本思想是将n个元素分成大致相等的两部分，取a[n/2]与x做比较，如果x=a[n/2],则找到x,算法中止；如果xa[n/2],则只要在数组a的右半部搜索x.

public class BinarySearch {
	public static int sort(int []array,int index,int low,int high){
        if(low<=high){
            int mid=(low+high)/2;
            if(index==array[mid]){
                return mid; //求目标元素的下标
            }
            else if(index>array[mid]){
                return sort(array,index,mid+1,high);
            }else{
                return sort(array,index,low,mid-1);
            }
        }
        return -1;
    }
	public static void main(String[] args){
		int a[]={1,3,4,5,6,7,8,10,34};
		System.out.println(sort(a,10,0,a.length-1));
	}
}

代码粘进代码框，格式有些问题，调整不了，逼死强迫症啊!啊！啊！！！