吴恩达Coursera深度学习(2-2)编程练习
Class 2:改善深层神经网络:超参数调试、正则化以及优化
Week 2:优化算法
目录
- Class 2:改善深层神经网络:超参数调试、正则化以及优化
- Week 2:优化算法
- 目录
- 1、梯度下降
- 2、Mini batch 梯度下降
- 3、Momentum动量项
- 4、Adam算法
- 5、不同的优化算法
import numpy as np
import matplotlib.pyplot as plt
import scipy.io
import math
import sklearn
import sklearn.datasets
from opt_utils import *
from testCases import *
# matplotlib inline
plt.rcParams['figure.figsize'] = (7.0, 4.0) # set default size of plots
plt.rcParams['image.interpolation'] = 'nearest'
plt.rcParams['image.cmap'] = 'gray'
# 1、梯度下降
def update_parameters_with_gd(parameters, grads, learning_rate):
L = len(parameters)//2
for l in range(L):
parameters["W"+str(l+1)] = parameters["W"+str(l+1)] - learning_rate * grads["dW"+str(l+1)]
parameters["b"+str(l+1)] = parameters["b"+str(l+1)] - learning_rate * grads["db"+str(l+1)]
return parameters
# 2、随机创建 mini batch
def random_mini_batches(X, Y, mini_batch_size=64, seed=0):
"""
Creates a list of random minibatches from (X, Y)
Arguments:
X -- input data, of shape (input size, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
mini_batch_size -- size of the mini-batches, integer
Returns:
mini_batches -- list of synchronous (mini_batch_X, mini_batch_Y)
"""
np.random.seed(seed)
m = X.shape[1]
mini_batches = []
# (1)shuffle(X, Y)
permutation = list(np.random.permutation(m)) # permutation 排列
shuffled_X = X[:, permutation]
shuffled_Y = Y[:, permutation].reshape((1,m))
# (2)partion(shuffled_X, shuffled_Y)
num_complete_mini_batches = math.floor(m/mini_batch_size)
for i in range(0, num_complete_mini_batches):
mini_batch_X = shuffled_X[:, i*mini_batch_size : (i+1)*mini_batch_size]
mini_batch_Y = shuffled_Y[:, i*mini_batch_size : (i+1)*mini_batch_size]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
# (3)处理尾部的样本(last mini batch < mini batch)
if m % mini_batch_size != 0:
mini_batch_X = shuffled_X[:, num_complete_mini_batches*mini_batch_size : m]
mini_batch_Y = shuffled_Y[:, num_complete_mini_batches*mini_batch_size : m]
mini_batch = (mini_batch_X, mini_batch_Y)
mini_batches.append(mini_batch)
return mini_batches
X_assess, Y_assess, mini_batch_size = random_mini_batches_test_case()
mini_batches = random_mini_batches(X_assess, Y_assess, mini_batch_size)
# 3-1、初始化 velocity
def initialize_velocity(parameters):
"""
Initializes the velocity as a python dictionary with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
Returns:
v -- python dictionary containing the current velocity.
v['dW' + str(l)] = velocity of dWl
v['db' + str(l)] = velocity of dbl
"""
L = len(parameters)//2
v = {}
for l in range(L):
v["dW" + str(l+1)] = np.zeros(parameters["W" + str(l+1)].shape)
v["db" + str(l+1)] = np.zeros(parameters["b" + str(l+1)].shape)
return v
# 3-2、带有动量项的参数更新
def update_parameters_with_momentum(parameters, grads, v, beta, learning_rate):
"""
Update parameters using Momentum
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- python dictionary containing the current velocity:
v['dW' + str(l)] = ...
v['db' + str(l)] = ...
beta -- the momentum hyperparameter, scalar
learning_rate -- the learning rate, scalar
Returns:
parameters -- python dictionary containing your updated parameters
v -- python dictionary containing your updated velocities
"""
L = len(parameters)//2
for l in range(L):
# 计算velocity
v["dW"+str(l+1)] = beta * v["dW"+str(l+1)] + (1-beta)* grads["dW"+str(l+1)]
v["db"+str(l+1)] = beta * v["db"+str(l+1)] + (1-beta)* grads["db"+str(l+1)]
# 更新参数
parameters["W"+str(l+1)] = parameters["W"+str(l+1)] - learning_rate * v["dW"+str(l+1)]
parameters["b"+str(l+1)] = parameters["b"+str(l+1)] - learning_rate * v["db"+str(l+1)]
return parameters, v
parameters, grads, v = update_parameters_with_momentum_test_case()
# 4-1、初始化adam的 v,s
def initialize_adam(parameters):
"""
Initializes v and s as two python dictionaries with:
- keys: "dW1", "db1", ..., "dWL", "dbL"
- values: numpy arrays of zeros of the same shape as the corresponding gradients/parameters.
Arguments:
parameters -- python dictionary containing your parameters.
parameters["W" + str(l)] = Wl
parameters["b" + str(l)] = bl
Returns:
v -- python dictionary that will contain the exponentially weighted average of the gradient.
v["dW" + str(l)] = ...
v["db" + str(l)] = ...
s -- python dictionary that will contain the exponentially weighted average of the squared gradient.
s["dW" + str(l)] = ...
s["db" + str(l)] = ...
"""
L = len(parameters)//2
v = {}
s = {}
for l in range(L):
v["dW"+str(l+1)] = np.zeros(parameters["W"+str(l+1)].shape)
v["db"+str(l+1)] = np.zeros(parameters["b"+str(l+1)].shape)
s["dW"+str(l+1)] = np.zeros(parameters["W"+str(l+1)].shape)
s["db"+str(l+1)] = np.zeros(parameters["b"+str(l+1)].shape)
return v, s
# 4-2、带有 Adam 的参数更新
def update_parameters_with_adam(parameters, grads, v, s, t, learning_rate=0.01,
beta1=0.9, beta2=0.999, epsilon=1e-8):
"""
Update parameters using Adam
Arguments:
parameters -- python dictionary containing your parameters:
parameters['W' + str(l)] = Wl
parameters['b' + str(l)] = bl
grads -- python dictionary containing your gradients for each parameters:
grads['dW' + str(l)] = dWl
grads['db' + str(l)] = dbl
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
learning_rate -- the learning rate, scalar.
beta1 -- Exponential decay hyperparameter for the first moment estimates
beta2 -- Exponential decay hyperparameter for the second moment estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
Returns:
parameters -- python dictionary containing your updated parameters
v -- Adam variable, moving average of the first gradient, python dictionary
s -- Adam variable, moving average of the squared gradient, python dictionary
"""
L = len(parameters)//2
v_corrected = {}
s_corrected = {}
for l in range(L):
v["dW"+str(l+1)] = beta1 * v["dW"+str(l+1)] + (1-beta1) * grads["dW"+str(l+1)]
v["db"+str(l+1)] = beta1 * v["db"+str(l+1)] + (1-beta1) * grads["db"+str(l+1)]
v_corrected["dW"+str(l+1)] = v["dW"+str(l+1)]/(1 - beta1**t)
v_corrected["db"+str(l+1)] = v["db"+str(l+1)]/(1 - beta1**t)
s["dW"+str(l+1)] = beta2 * s["dW"+str(l+1)] + (1-beta2) * (grads["dW"+str(l+1)]**2)
s["db"+str(l+1)] = beta2 * s["db"+str(l+1)] + (1-beta2) * (grads["db"+str(l+1)]**2)
s_corrected["dW"+str(l+1)] = s["dW"+str(l+1)]/(1 - beta2**t)
s_corrected["db"+str(l+1)] = s["db"+str(l+1)]/(1 - beta2**t)
parameters["W"+str(l+1)] = parameters["W"+str(l+1)] - learning_rate * (v_corrected["dW"+str(l+1)]/(np.sqrt(s_corrected["dW"+str(l+1)])+epsilon))
parameters["b"+str(l+1)] = parameters["b"+str(l+1)] - learning_rate * (v_corrected["db"+str(l+1)]/(np.sqrt(s_corrected["db"+str(l+1)])+epsilon))
return parameters, v, s
# 5、神经网络模型
def model(X, Y, layers_dims, optimizer, learning_rate=0.001, num_epochs=10000, mini_batch_size=64,
beta=0.9, beta1=0.9, beta2=0.999, epsilon=1e-8, print_cost=True):
"""
3-layer neural network model which can be run in different optimizer modes.
Arguments:
X -- input data, of shape (2, number of examples)
Y -- true "label" vector (1 for blue dot / 0 for red dot), of shape (1, number of examples)
layers_dims -- python list, containing the size of each layer
learning_rate -- the learning rate, scalar.
mini_batch_size -- the size of a mini batch
num_epochs -- number of epochs
print_cost -- True to print the cost every 1000 epochs
beta -- Momentum hyperparameter
beta1 -- Exponential decay hyperparameter for the past gradients estimates
beta2 -- Exponential decay hyperparameter for the past squared gradients estimates
epsilon -- hyperparameter preventing division by zero in Adam updates
Returns:
parameters -- python dictionary containing your updated parameters
"""
L = len(layers_dims)
costs = []
t = 0
seed = 10
# 初始化参数
parameters = initialize_parameters(layers_dims)
# 初始化优化器
if optimizer == "gd":
pass
elif optimizer =="momentum":
v = initialize_velocity(parameters)
elif optimizer == "adam":
t = t + 1 # Adam counter
v,s = initialize_adam(parameters)
# optimization loop
for i in range(num_epochs):
# 重新打乱(X,Y)
seed = seed + 1
mini_batches = random_mini_batches(X, Y, mini_batch_size, seed)
for mini_batch in mini_batches:
# 选择一个 mini_batch
(mini_batch_X, mini_batch_Y) = mini_batch
# 前向传播
a3, caches = forward_propagation(mini_batch_X, parameters)
# 计算损失函数
cost = compute_cost(a3, mini_batch_Y)
# 后向传播
grads = backward_propagation(mini_batch_X, mini_batch_Y, caches)
# 更新参数
if optimizer == "gd":
parameters = update_parameters_with_gd(parameters, grads, learning_rate)
elif optimizer == "momentum":
parameters, v = update_parameters_with_momentum(parameters, grads, v, beta, learning_rate)
elif optimizer == "adam":
parameters, v, s == update_parameters_with_adam(parameters, grads, v, s, t,
learning_rate, beta1, beta2, epsilon)
if print_cost and i%100==0:
costs.append(cost)
print("cost after epoch %i : %f" % (i, cost))
plt.plot(costs)
plt.ylabel('cost')
plt.xlabel('epochs (per 100)')
plt.title("learning rate = " + str(learning_rate))
plt.show()
return parameters
# 6、下载数据
train_X, train_Y = load_dataset()
plt.show()
# 7、测试模型
# train 3-layer model
layers_dims = [train_X.shape[0], 5, 2, 1]
#====================================================== 选择不同优化器
#parameters = model(train_X, train_Y, layers_dims, optimizer = "gd")
#parameters = model(train_X, train_Y, layers_dims, beta = 0.9, optimizer = "momentum")
parameters = model(train_X, train_Y, layers_dims, optimizer = "adam")
# Predict
predictions = predict(train_X, train_Y, parameters)
# Plot decision boundary
plt.title("Model with Gradient Descent optimization")
axes = plt.gca()
axes.set_xlim([-1.5,2.5])
axes.set_ylim([-1,1.5])
plot_decision_boundary(lambda x: predict_dec(parameters, x.T), train_X, train_Y)一直使用梯度下降法更新参数、最小化代价函数
使用优化算法,加速学习,或许能得到一个更好的代价函数
1、梯度下降
在随机梯度下降中,在更新梯度之前,只使用1个训练样例
当训练集大时,SGD可以更快,但是这些参数会向最小值“摆动”,而不是平稳的收敛
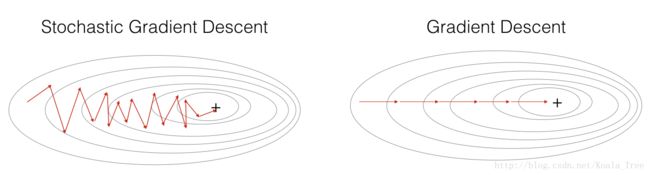
+表示成本的最小值,随机梯度下降导致很多的波动达到收敛
但是,SGD每一步比GD要快的多,因为GD使用所有样本更新,SGD只使用一个样本更新
- 注意:SGD需要三个循环,所有的迭代次数、所有的训练样本、所有的层
2、Mini batch 梯度下降
在实际中,既不使用所有样本更新参数,也不使用一个样本更新参数
小批量梯度下降,可以循环使用小批量,小批量通常导致更快的优化
如何构建 mini batch,有两步:
- (1)shuffle打乱
- (2)partion分区
Mini batch 通常的大小是 16, 32, 64, 128
假设Mini_batch_size = 64, 训练样本的数量不一定能整除mini_batch_size,最后一个小块可能会小一点
3、Momentum动量项
小批量梯度下降仅在看到一个子集的样本后,就进行参数更新,因此更新的方向有一定的变化,小批量梯度下降的路径将要震荡的收敛,使用动量项能减少这些震荡。
动量是考虑之前的梯度gradients来平滑更新,我们要存储之前在变量“v”上的梯度方向。形式上,是将前面步骤中的梯度进行指数平均加权。可以把“V”看作是一个下坡滚动的速度,根据山坡的坡度/方向建立速度(和动量)。

红色箭头表示一步加动量的小批量梯度下降的方向
蓝色点显示每一步梯度的方向(相当于当前小批量)
我们让梯度影响“V”,然后向“V”的方向走一步,而不是仅仅的跟随梯度
- 初始化速度,速度V是一个字典,键与grads字典一样,需要被初始化为0
4、Adam算法

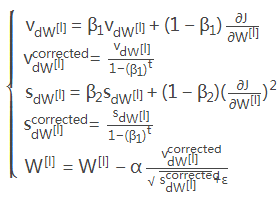

初始化Adam变量v, s 保持追踪过去的信息
速度V,S是一个字典,键与grads字典一样,需要被初始化为0
for l in range(L):
v["dW"+str(l+1)] = np.zeros(parameters["W"+str(l+1)].shape)
v["db"+str(l+1)] = np.zeros(parameters["b"+str(l+1)].shape)
s["dW"+str(l+1)] = np.zeros(parameters["W"+str(l+1)].shape)
s["db"+str(l+1)] = np.zeros(parameters["b"+str(l+1)].shape)for l in range(L):
v["dW"+str(l+1)] = beta1 * v["dW"+str(l+1)] + (1-beta1) * grads["dW"+str(l+1)]
v["db"+str(l+1)] = beta1 * v["db"+str(l+1)] + (1-beta1) * grads["db"+str(l+1)]
v_corrected["dW"+str(l+1)] = v["dW"+str(l+1)]/(1 - beta1**t)
v_corrected["db"+str(l+1)] = v["db"+str(l+1)]/(1 - beta1**t)
s["dW"+str(l+1)] = beta2 * s["dW"+str(l+1)] + (1-beta2) * (grads["dW"+str(l+1)]**2)
s["db"+str(l+1)] = beta2 * s["db"+str(l+1)] + (1-beta2) * (grads["db"+str(l+1)]**2)
s_corrected["dW"+str(l+1)] = s["dW"+str(l+1)]/(1 - beta2**t)
s_corrected["db"+str(l+1)] = s["db"+str(l+1)]/(1 - beta2**t)
parameters["W"+str(l+1)] = parameters["W"+str(l+1)] - learning_rate * (v_corrected["dW"+str(l+1)]/(np.sqrt(s_corrected["dW"+str(l+1)])+epsilon))
parameters["b"+str(l+1)] = parameters["b"+str(l+1)] - learning_rate * (v_corrected["db"+str(l+1)]/(np.sqrt(s_corrected["db"+str(l+1)])+epsilon))5、不同的优化算法
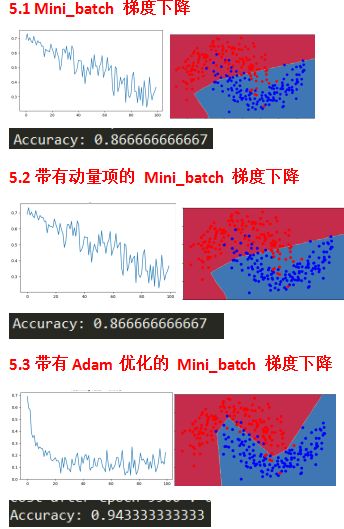
动量通常是有帮助的,但由于学习率低、数据集简单,其影响几乎可以忽略不计。
另外,由于实际成本函数震荡巨大,一些mini batches对于优化算法更困难。
Adam显然优于mini batch和momentum,如果迭代次数足够多,3种模型都能得到很好的结果,但是Adam收敛的更快
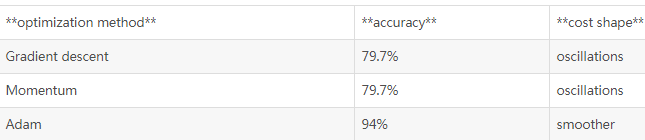
Adam的优点:
- 相对更低的内存要求,(虽然高于momentum和mini batch)
- 通常微调超参数,就可以得到很好的结果(Learning rate除外)