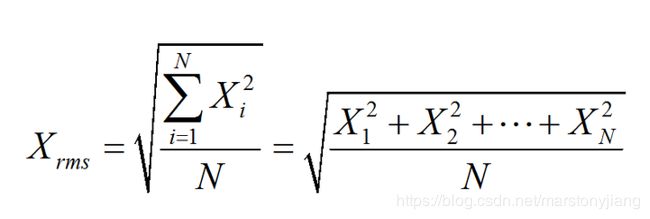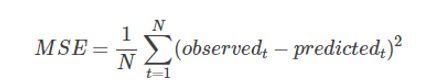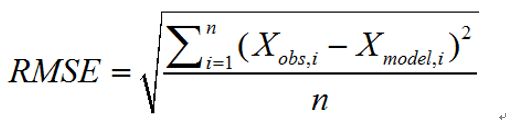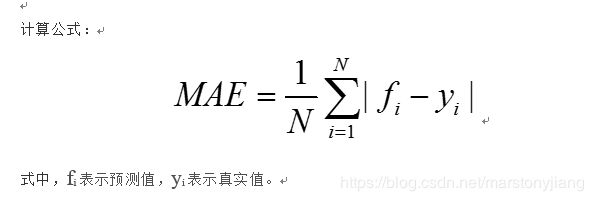数学分析方法——各种误差分析的区别总结
总结:
(1)相同:
标准差=标准偏差=均方差=实验标准差;
均方根误差=标准误差;
均方根值=方均根值=有效值
(2)不同
均方差≠均方误差
(3)标准差(std):标准差定义是观测值与其平均数偏差的平方和求平均后的平方根。它反映组内个体间的离散程度。均方根误差(RMSE,root mean square error):它是观测值与真值偏差的平方和观测次数n比值的平方根。它们的研究对象和研究目的不同,但是计算过程类似。
1.1 均方根值(Root Mean Square,RMS)
均方根值,也称作方均根值或有效值。
美国传统词典的定义为:The square root of the average of squares of a set of numbers.即:将N个项的平方和除以N后开平方的结果,即均方根的结果。
计算公式为:
1.2 方差(variance)
参见网上解释,此处略。
1.3 标准差(Standard Deviation, SD)
- 概念解析
标准差是方差的算术平方根,也称均方差(注意这里不是均方误差),也被称为标准偏差,或者实验标准差。
标准差的定义是各数据值与其平均数之差的平方的算术平均数的平方根,即离均差的平方和求平均后的方根,用σ表示,标准差能反映一个数据集的离散程度。平均数相同的两组数据,标准差未必相同。
简单来说,标准差是一组数据平均值分散程度的一种度量。一个较大的标准差,代表大部分数值和其平均值之间差异较大;一个较小的标准差,代表这些数值较接近平均值。标准差反映数值相对于平均值 (mean) 的离散程度。
- 注意
(1)离均差是指各数据偏离平均数的距离。
(2)均方差不同于均方误差(Mean Squared Error,MSE)。
均方误差是各数据偏离真实值的距离平方和的平均数,也即误差平方和的平均数,计算公式形式上接近方差,它的开方叫均方根误差,均方根误差才和标准差形式上接近))
- 例子
(1)例如,A、B两组各有6位学生参加同一次语文测验,A组的分数为95、85、75、65、55、45,B组的分数为73、72、71、69、68、67.这两组的平均数都是70,但A组的标准差为17.08分,B组的标准差为2.16分,说明A组学生之间的差距要比B组学生之间的差距大得多.
- 软件中的求解方法
在matlab中,用std函数来计算标准差。
在Excel2013中的求解方法,查阅网上资料。
1.4 均方误差(Mean Squared Error,MSE)
均方误差是各数据偏离真实值的距离平方和的平均数
1.5 均方根误差(Root Mean Square Error,RMSE)
均方根误差,亦称标准误差。
均方根误差是均方误差的算术平方根,它是观测值与真值偏差的平方和与观测次数n比值的平方根,在实际测量中,观测次数n总是有限的,真值只能用最可信赖(最佳)值来代替。均方根误差对一组测量中的特大或特小误差反映非常敏感,所以,均方根误差能够很好地反映出测量的精密度。
1.6 平均绝对误差(Mean Absolute Error,MAE)
- 概念解析
平均绝对误差(Mean Absolute Error,MAE)是绝对误差的平均值。MAE用来表示预测值与真实值之间平均相差多大。
平均绝对误差能更好地反映预测值误差的实际情况。
- 注意
(1)MAD(mean absolute deviation)与MAE(Mean Absolute Error)有点区别。总的来说,MAD表示的范围比MAE更广些。(百度百科上的“平均绝对误差”理解为MAD,这是不对的)
MAE: https://en.wikipedia.org/wiki/Mean_absolute_error
MAD: https://en.wikipedia.org/wiki/Average_absolute_deviation
(2)在测量预测误差时,Mean Absolute Deviation (MAD)和 Mean Absolute Error (MAE)被当作同一种方法(http://www.vanguardsw.com/business-forecasting-101/mean-absolute-deviation-mad-mean-absolute-error-mae/)。
1.7 平均相对误差(Mean Relative Error,MRE)
这点在该文献(潘竟虎 et al. 2014)有提到,但未解释其求法,且在网上还没找到好的解释(待完善)
1.8 平均误差(mean error,ME)
这点在该文献(潘竟虎 et al. 2014)有提到,但未解释其求法,且在网上还没找到好的解释(待完善)
参考文献:
[1] 潘竟虎, 张文, 李俊峰, 文岩, 王春娟. 中国大范围雾霾期间主要城市空气污染物分布特征[J]. 生态学杂志, 2014, 33(12): 3423-3431.