python3 15.tensorflow使用卷积神经网络(CNN)对MNIST数据集进行分类 学习笔记

前言

     计算机视觉系列之学习笔记主要是本人进行学习人工智能（计算机视觉方向）的代码整理。本系列所有代码是用python3编写，在平台Anaconda中运行实现，在使用代码时，默认你已经安装相关的python库，这方面不做多余的说明。本系列所涉及的所有代码和资料可在我的github上下载到，gitbub地址：https://github.com/mcyJacky/DeepLearning-CV，如有问题，欢迎指出。

一、卷积神经网络CNN优势

     在关于图像处理等神经网络中，卷积神经网络（Convolutional neural network）是一种常用的方式，具体卷积使用过程中的原理本篇不做详细的介绍。与传统BP神经网络相比，CNN的优势有：

• 参数共享 parameter sharing
• 稀疏连接 sparsity of connections

图1.1 卷积操作示例

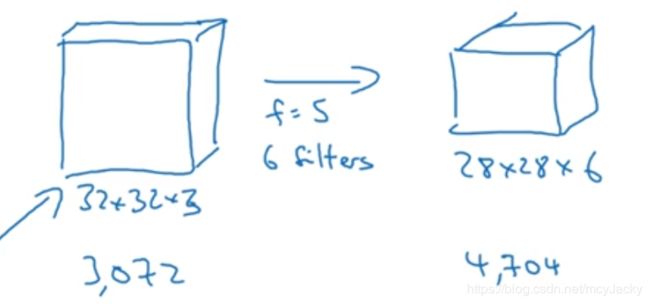
如图1.1所示，输入图为：32x32x3，通过卷积操作后输出图：28x28x6。则共有计算参数有卷积核参数5*5 = 25个，偏置参数为1个，共有6个卷积核则共有参数(25+1)*6 = 156个参数。而如果输入和输出是传统BP网络，则共有参数约32x32x3 x 28x28x6 ≈14000000个。可以看出使用CNN可以有效的减少神经网络训练需要的参数个数。

二、模拟LeNet-5网络结构对MNIST数据集分类

     LeNet-5模型是非常经典的CNN网络，它的网络结构图如下图2.1所示：

图2.1 LeNet-5网络结构

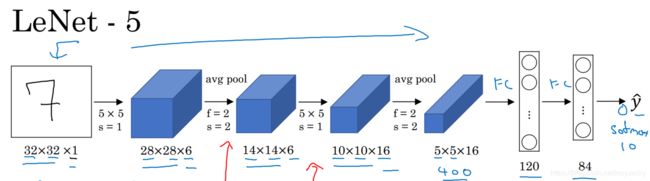
     该网络的输入为32x32x1结构，然后进行卷积-平均池化-卷积-平均池化-全连接-全连接-softmax输出。MNIST数据集的输入为28x28x1结构，下面通过tensorflow建立CNN网络对MNIST数据集分类(该网络与LeNet-5不完全一样):

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data

# 载入数据
mnist = input_data.read_data_sets('MNIST_data', one_hot=True)
# 每次批次的大小
batch_size = 64
# 训练数据每个周期有多少批次
n_batch = mnist.train.num_examples // batch_size

# 定义两个placeholder
x = tf.placeholder(tf.float32, [None,784])
y = tf.placeholder(tf.float32, [None,10])

# 权值初始化(卷积中为卷积核)
def weight_variable(shape):
    # 生成一个截断的正态分布
    initial = tf.truncated_normal(shape, stddev=0.2)
    return tf.Variable(initial)

# 偏置初始化
def bias_variable(shape):
    initial = tf.constant(0.1, shape=shape)
    return tf.Variable(initial)

# 卷积层
def conv2d(x, W):
    # x: input tensor of shape. [batch, in_height, in_width, in_channels]
    # W: filter of tensor [filter_height, filter_width, in_channels, out_channels]
    # strides[0] = strides[3] = 1, strides[1]:表示x方向步长， strides[2]:表示y方向步长
    # padding: 'string' from 'SAME', 'VALID'
    return tf.nn.conv2d(x, W, strides=[1,1,1,1], padding='SAME')


# 池化层
def max_pool_2x2(x):
    # x: 池化对象
    #ksize: 池化层的尺寸[batch, in_height, in_width, in_channels]
    #strides[0] = strides[3] = 1, strides[1]:表示x方向步长， strides[2]:表示y方向步长
    # padding: 'string' from 'SAME', 'VALID'
    return tf.nn.max_pool(x, ksize=[1,2,2,1], strides=[1,2,2,1], padding='VALID')

# 将输入图片x格式转化为4D格式 [batch, in_height, in_width, in_channels]
# -1表示匹配所有批次
x_image = tf.reshape(x,[-1,28,28,1])

# 初始化第一个卷积层的权值和偏置 28x28x1 -> 28x28x32
W_conv1 = weight_variable([5,5,1,32]) # 过滤器尺寸:5x5x1 过滤器数量为32
b_conv1 = bias_variable([32])
# 把x_image和权值向量进行卷积，再加上偏置值，然后用relu激活函数
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
# 进行max_pooling 28x28x32 -> 14x14x32
h_pool1 = max_pool_2x2(h_conv1)

# 初始化第二个卷积层的权值和偏置 14x14x32 -> 14x14x64
W_conv2 = weight_variable([5,5,32,64]) # 5x5x32 过滤器数量为32
b_conv2 = bias_variable([64])
# 把h_pool1和权值向量进行卷积，再加上偏置值，然后应用于relu激活函数
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2)
# 进行max_pooling 14x14x64 -> 7x7x64
h_pool2 = max_pool_2x2(h_conv2)

# 28*28的图片第一次卷积后还是28*28，第一次池化后变为14*14
# 第二次卷积后为14*14，第二次池化后变为了7*7
# => 进过上面操作后得到7*7*64
# 初始化第一个FC全连接层的权值
W_fc1 = weight_variable([7*7*64,1024])
b_fc1 = bias_variable([1024])
# 把池化层2的输出扁平化为1维
h_pool2_flat = tf.reshape(h_pool2, [-1,7*7*64])
# 第一个连接层的输出
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
# 使用dropout
keep_prob = tf.placeholder(tf.float32)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)

# 初始化第二个FC全连接层
W_fc2 = weight_variable([1024,10])
b_fc2 = bias_variable([10])
# 计算输出
prediction = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)

# 定义交叉熵代价函数
cross_entropy = tf.losses.softmax_cross_entropy(y, prediction)
# 优化器
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)

# 结果存放在一个布尔列表中
correct_prediction = tf.equal(tf.argmax(prediction,1), tf.argmax(y,1))
# 准确率
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))

# 定义会话
with tf.Session() as sess:
    sess.run(tf.global_variables_initializer())
    for epoch in range(21):
        for batch in range(n_batch):
            batch_xs, batch_ys = mnist.train.next_batch(batch_size)
            sess.run(train_step, feed_dict={x:batch_xs, y:batch_ys, keep_prob:0.7})
        
        acc = sess.run(accuracy, feed_dict={x:mnist.test.images,y:mnist.test.labels, keep_prob:1.0})
        print('iter: '+ str(epoch) + " test accuracy: " + str(acc))

#部分输出结果：
# Iter 0, Testing Accuracy= 0.9634
# Iter 1, Testing Accuracy= 0.9775
# Iter 2, Testing Accuracy= 0.9785
# Iter 3, Testing Accuracy= 0.9844
# Iter 4, Testing Accuracy= 0.9862
# Iter 5, Testing Accuracy= 0.9863
# ...
# Iter 14, Testing Accuracy= 0.9893
# Iter 15, Testing Accuracy= 0.9899
# Iter 16, Testing Accuracy= 0.9892
# Iter 17, Testing Accuracy= 0.9913
# Iter 18, Testing Accuracy= 0.9918
# Iter 19, Testing Accuracy= 0.9915
# Iter 20, Testing Accuracy= 0.9908

     通过训练结果可知，使用CNN对MNIST数据集分类的效果比BP神经网络要好很多，准确率已经高于99%。LeNet-5网络模型也是一个比较简单的CNN模型，以后会介绍更多深度卷积经典网络。

     
     
     
     
【参考】：
     1. 城市数据团课程《AI工程师》计算机视觉方向
     2. deeplearning.ai 吴恩达《深度学习工程师》
     3. 《机器学习》作者：周志华
     4. 《深度学习》作者：Ian Goodfellow

---

转载声明：
版权声明：非商用自由转载-保持署名-注明出处
署名 ：mcyJacky
文章出处：https://blog.csdn.net/mcyJacky