python 数据挖掘
第一节
介绍
数据挖掘是一个隐式提取以前未知的潜在有用的数据信息提取方式。它使用广泛,并且是众多应用的技术基础。
本文介绍那些使用Python数据挖掘实践用于发现和描述结构模式数据的工具。近些年来,Python在开发以数据为中心的应用中被用的越来越多。感谢大型科学计算社区的支持以及大大丰富的数据分析函数库。尤其是,我们可以看到如何:
• 导入和可视化数据
• 数据分类
• 使用回归分析和相关测量法发现数据之间的关系
• 数据降维以压缩和可视化数据带来的信息
• 分析结构化数据
每个主题都会提供代码实例,它们基于四个主要的Python数据分析和处理的类库:numpy,matplotlib,sklearn和networkx。
第二节
数据导入和可视化
通常,数据分析的第一步由获取数据和导入数据到我们的工作环境组成。我们可以使用以下的Python代码简单的下载数据:
|
1
2
3
4
5
6
|
import
urllib2
url
=
'http://aima.cs.berkeley.edu/data/iris.csv'
u
=
urllib2
.
urlopen
(
url
)
localFile
=
open
(
'iris.csv'
', '
w'
)
localFile
.
write
(
u
.
read
(
)
)
localFile
.
close
(
)
|
在以上的代码片段中,我们使用了urllib2类库以获取伯克利大学网站的一个文件,并使用标准类库提供的File对象把它保存到本地磁盘。数据包含鸢尾花(iris)数据集,这是一个包含了三种鸢尾花(山鸢尾、维吉尼亚鸢尾和变色鸢尾)的各50个数据样本的多元数据集,每个样本都有四个特征(或者说变量),即花萼(sepal)和花瓣(petal)的长度和宽度。以厘米为单位。
数据集以CSV(逗号分割值)的格式存储。CSV文件可以很方便的转化并把其中的信息存储为适合的数据结构。此数据集有5列(译者注:原文是行,但这里应该是列的意思),前4列包含着特征值,最后一列代表着样本类型。CSV文件很容易被numpy类库的genfromtxt方法解析:
|
1
2
3
4
5
|
from
numpy
import
genfromtxt
,
zeros
# read the first 4 columns
data
=
genfromtxt
(
'iris.csv'
,
delimiter
=
','
,
usecols
=
(
0
,
1
,
2
,
3
)
)
# read the fifth column
target
=
genfromtxt
(
'iris.csv'
,
delimiter
=
','
,
usecols
=
(
4
)
,
dtype
=
str
)
|
在上面的例子中我们创建了一个包含特征值的矩阵以及一个包含样本类型的向量。我们可以通过查看我们加载的数据结构的shape值来确认数据集的大小:
|
1
2
3
4
|
print
data
.
shape
(
150
,
4
)
print
target
.
shape
(
150
,
)
|
我们也可以查看我们有多少种样本类型以及它们的名字:
|
1
2
|
print
set
(
target
)
# build a collection of unique elements
set
(
[
'setosa'
,
'versicolor'
,
'virginica'
]
)
|
当我们处理新数据的时候,一项很重要的任务是尝试去理解数据包含的信息以及它的组织结构。可视化可以灵活生动的展示数据,帮助我们深入理解数据。
使用pylab类库(matplotlib的接口)的plotting方法可以建一个二维散点图让我们在两个维度上分析数据集的两个特征值:
|
1
2
3
4
5
|
from
pylab
import
plot
,
show
plot
(
data
[
target
==
'setosa'
,
0
]
,
data
[
target
==
'setosa'
,
2
]
,
'bo'
)
plot
(
data
[
target
==
'versicolor'
,
0
]
,
data
[
target
==
'versicolor'
,
2
]
,
'ro'
)
plot
(
data
[
target
==
'virginica'
,
0
]
,
data
[
target
==
'virginica'
,
2
]
,
'go'
)
show
(
)
|
上面那段代码使用第一和第三维度(花萼的长和宽),结果如下图所示: 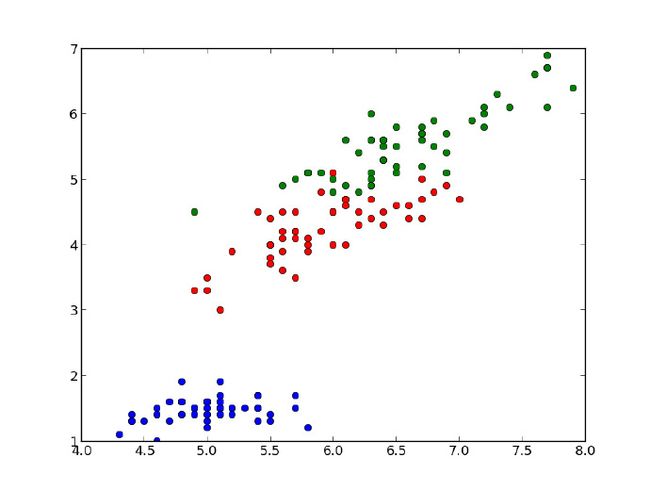
在上图中有150个点,不同的颜色代表不同的类型;蓝色点代表山鸢尾,红色点代表变色鸢尾,绿色点代表维吉尼亚鸢尾。
另一种常用的查看数据的方法是分特性绘制直方图。在本例中,既然数据被分为三类,我们就可以比较每一类的分布特征。下面这个代码可以绘制数据中每一类型的第一个特性(花萼的长度):
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
|
from
pylab
import
figure
,
subplot
,
hist
,
xlim
,
show
xmin
=
min
(
data
[
:
,
0
]
)
xmax
=
max
(
data
[
:
,
0
]
)
figure
(
)
subplot
(
411
)
# distribution of the setosa class (1st, on the top)
hist
(
data
[
target
==
'setosa'
,
0
]
,
color
=
'b'
,
alpha
=
.
7
)
xlim
(
xmin
,
xmax
)
subplot
(
412
)
# distribution of the versicolor class (2nd)
hist
(
data
[
target
==
'versicolor'
,
0
]
,
color
=
'r'
,
alpha
=
.
7
)
xlim
(
xmin
,
xmax
)
subplot
(
413
)
# distribution of the virginica class (3rd)
hist
(
data
[
target
==
'virginica'
,
0
]
,
color
=
'g'
,
alpha
=
.
7
)
xlim
(
xmin
,
xmax
)
subplot
(
414
)
# global histogram (4th, on the bottom)
hist
(
data
[
:
,
0
]
,
color
=
'y'
,
alpha
=
.
7
)
xlim
(
xmin
,
xmax
)
show
(
)
|
结果如下图:
根据上图的直方图,我们可以根据数据类型区分理解数据的特征。例如,我们可以观察到,山鸢尾的平均花萼长度小于维吉尼亚鸢尾。
第三节
分类
分类是一个数据挖掘方法,用于把一个数据集中的样本数据分配给各个目标类。实现这个方法的模块叫做分类器。使用分类器需要以下两步:训练和分类。训练是指采集已知其特定类归属的数据并基于这些数据创建分类器。 分类是指使用通过这些已知数据建立的分类器来处理未知的数据,以判断未知数据的分类情况。
Sklearn类库包含很多分类器的实现,本章我们将会使用高斯朴素贝叶斯来分析我们在第一章载入的鸢尾花数据,包含山鸢尾、变色鸢尾和维吉尼亚鸢尾。最后我们把字符串数组转型成整型数据:
|
1
2
3
4
|
t
=
zeros
(
len
(
target
)
)
t
[
target
==
'setosa'
]
=
1
t
[
target
==
'versicolor'
]
=
2
t
[
target
==
'virginica'
]
=
3
|
现在我们已经做好实例化和训练分类器的准备了:
|
1
2
3
|
from
sklearn
.
naive_bayes
import
GaussianNB
classifier
=
GaussianNB
(
)
classifier
.
fit
(
data
,
t
)
# training on the iris dataset
|
分类器可以由predict方法完成,并且只要输出一个样例就可以很简单的检测:
|
1
2
3
4
|
print
classifier
.
predict
(
data
[
0
]
)
[
1.
]
print
t
[
0
]
1
|
上例中predicted类包含了一个正确的样本(山鸢尾),但是在广泛的样本上评估分类器并且使用非训练环节的数据测试是很重要的。最终我们通过从源数据集中随机抽取样本把数据分为训练集和测试集。我们将会使用训练集的数据来训练分类器,并使用测试集的数据来测试分类器。train_test_split方法正是实现此功能的:
|
1
2
3
|
from
sklearn
import
cross_validation
train
,
test
,
t_train
,
t_test
=
cross_validation
.
train_test_split
(
data
,
t
,
…
test_size
=
0.4
,
random_state
=
0
)
|
数据集被分一分为二,测试集被指定为源数据的40%(命名为test_size),我们用它反复训练我们的分类器并输出精确度:
|
1
2
3
|
classifier
.
fit
(
train
,
t_train
)
# train
print
classifier
.
score
(
test
,
t_test
)
# test
0.93333333333333335
|
在此例中,我们的精确度为93%。一个分类器的精确度是通过正确分类样本的数量除以总样本的数量得出的。也就是说,它意味着我们正确预测的比例。
另一个估计分类器表现的工具叫做混淆矩阵。在此矩阵中每列代表一个预测类的实例,每行代表一个实际类的实例。使用它可以很容易的计算和打印矩阵:
|
1
2
3
4
5
|
from
sklearn
.
metrics
import
confusion_matrix
print
confusion_matrix
(
classifier
.
predict
(
test
)
,
t_test
)
[
[
16
0
0
]
[
0
23
3
]
[
0
0
18
]
]
|
在这个混淆矩阵中我们可以看到所有山鸢尾和维吉尼亚鸢尾都被正确的分类了,但是实际上应该是26个的变色鸢尾,系统却预测其中三个是维吉尼亚鸢尾。如果我们牢记所有正确的猜测都在表格的对角线上,那么观测表格的错误就很容易了,即对角线以外的非零值。
可以展示分类器性能的完整报告的方法也是很好用的:
|
1
2
3
4
5
6
7
|
from
sklearn
.
metrics
import
classification_report
print
classification_report
(
classifier
.
predict
(
test
)
,
t_test
,
target_names
=
[
'setosa'
,
'versicolor'
,
'virginica'
]
)
precision
recall
f1
-
score
support
setosa
1.00
1.00
1.00
16
versicolor
1.00
0.85
0.92
27
virginica
0.81
1.00
0.89
17
avg
/
total
0.95
0.93
0.93
60
|
以下是该报告使用到的方法总结:
Precision:正确预测的比例
Recall(或者叫真阳性率):正确识别的比例
F1-Score:precision和recall的调和平均数
以上仅仅只是给出用于支撑测试分类的数据量。当然,分割数据、减少用于训练的样本数以及评估结果等操作都依赖于配对的训练集和测试集的随机选择。如果要切实评估一个分类器并与其它的分类器作比较的话,我们需要使用一个更加精确的评估模型,例如Cross Validation。该模型背后的思想很简单:多次将数据分为不同的训练集和测试集,最终分类器评估选取多次预测的平均值。这次,sklearn为我们提供了运行模型的方法:
|
1
2
3
4
5
|
from
sklearn
.
cross_validation
import
cross_val_score
# cross validation with 6 iterations
scores
=
cross_val_score
(
classifier
,
data
,
t
,
cv
=
6
)
print
scores
[
0.84
0.96
1.
1.
1.
0.96
]
|
如上所见,输出是每次模型迭代产生的精确度的数组。我们可以很容易计算出平均精确度:
|
1
2
3
|
from
numpy
import
mean
print
mean
(
scores
)
0.96
|
第四章
聚类
通常我们的数据上不会有标签告诉我们它的样本类型;我们需要分析数据,把数据按照它们的相似度标准分成不同的群组,群组(或者群集)指的是相似样本的集合。这种分析被称为无监督数据分析。最著名的聚类工具之一叫做k-means算法,如下所示:
|
1
2
3
|
from
sklearn
.
cluster
import
KMeans
kmeans
=
KMeans
(
k
=
3
,
init
=
'random'
)
# initialization
kmeans
.
fit
(
data
)
# actual execution
|
上述片段运行k-measn算法并把数据分为三个群集(参数k所指定的)。现在我们可以使用模型把每一个样本分配到三个群集中:
|
1
|
c
=
kmeans
.
predict
(
data
)
|
我们可以估计群集的结果,与使用完整性得分和同质性得分计算而得的标签作比较:
|
1
2
3
4
5
|
from
sklearn
.
metrics
import
completeness_score
,
homogeneity_score
print
completeness_score
(
t
,
c
)
0.7649861514489815
print
homogeneity_score
(
t
,
c
)
0.7514854021988338
|
当大部分数据点属于一个给定的类并且属于同一个群集,那么完整性得分就趋向于1。当所有群集都几乎只包含某个单一类的数据点时同质性得分就趋向于1.
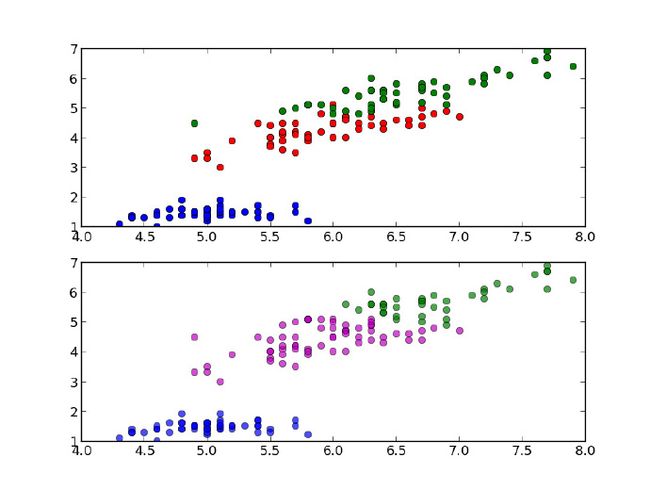
我们可以把集群可视化并和带有真实标签的做可视化比较:
|
1
2
3
4
5
6
7
8
9
10
|
figure
(
)
subplot
(
211
)
# top figure with the real classes
plot
(
data
[
t
==
1
,
0
]
,
data
[
t
==
1
,
2
]
,
'bo'
)
plot
(
data
[
t
==
2
,
0
]
,
data
[
t
==
2
,
2
]
,
'ro'
)
plot
(
data
[
t
==
3
,
0
]
,
data
[
t
==
3
,
2
]
,
'go'
)
subplot
(
212
)
# bottom figure with classes assigned automatically
plot
(
data
[
c
==
1
,
0
]
,
data
[
tt
==
1
,
2
]
,
'bo'
,
alpha
=
.
7
)
plot
(
data
[
c
==
2
,
0
]
,
data
[
tt
==
2
,
2
]
,
'go'
,
alpha
=
.
7
)
plot
(
data
[
c
==
0
,
0
]
,
data
[
tt
==
0
,
2
]
,
'mo'
,
alpha
=
.
7
)
show
(
)
|
结果如下图所示:
观察此图我们可以看到,底部左侧的群集可以被k-means完全识别,然而顶部的两个群集有部分识别错误。
第五章
回归
回归是一个用于预测变量之间函数关系调查的方法。例如,我们有两个变量,一个被认为是解释,一个被认为是依赖。我们希望使用模型描述两者的关系。当这种关系是一条线的时候就称为线性回归。
为了应用线性回归我们建立一个由上所述的综合数据集:
|
1
2
3
|
from
numpy
.
random
import
rand
x
=
rand
(
40
,
1
)
# explanatory variable
y
=
x
*
x
*
x
+
rand
(
40
,
1
)
/
5
# depentend variable
|
我们可以使用在sklear.linear_model模块中发现的LinearRegression模型。该模型可以通过计算每个数据点到拟合线的垂直差的平方和,找到平方和最小的最佳拟合线。使用方法和我们之前遇到的实现sklearn的模型类似:
|
1
2
3
|
from
sklearn
.
linear_model
import
LinearRegression
linreg
=
LinearRegression
(
)
linreg
.
fit
(
x
,
y
)
|
我们可以通过把拟合线和实际数据点画在同一幅图上来评估结果:
|
1
2
3
4
|
from
numpy
import
linspace
,
matrix
xx
=
linspace
(
0
,
1
,
40
)
plot
(
x
,
y
,
'o'
,
xx
,
linreg
.
predict
(
matrix
(
xx
)
.
T
)
,
'--r'
)
show
(
)
|
图见下:
观察该图我们可以得出结论:拟合线从数据点中心穿过,并可以确定是增长的趋势。
我们还可以使用均方误差来量化模型和原始数据的拟合度:
|
1
2
3
|
from
sklearn
.
metrics
import
mean_squared_error
print
mean_squared_error
(
linreg
.
predict
(
x
)
,
y
)
0.01093512327489268
|
该指标度量了预期的拟合线和真实数据之间的距离平方。当拟合线很完美时该值为0。
第六章
相关
我们通过研究相关性来理解成对的变量之间是否相关,相关性的强弱。此类分析帮助我们精确定位被依赖的重要变量。最好的相关方法是皮尔逊积矩相关系数。它是由两个变量的协方差除以它们的标准差的乘积计算而来。我们将鸢尾花数据集的变量两两组合计算出其系数如下所示:
|
1
2
3
4
5
6
7
|
from
numpy
import
corrcoef
corr
=
corrcoef
(
data
.
T
)
# .T gives the transpose
print
corr
[
[
1.
-
0.10936925
0.87175416
0.81795363
]
[
-
0.10936925
1.
-
0.4205161
-
0.35654409
]
[
0.87175416
-
0.4205161
1.
0.9627571
]
[
0.81795363
-
0.35654409
0.9627571
1.
]
]
|
corrcoef方法通过输入行为变量列为观察值的矩阵,计算返回相关系数的对称矩阵。该矩阵的每个元素代表着两个变量的相关性。
当值一起增长时相关性为正。当一个值减少而另一个只增加时相关性为负。特别说明,1代表完美的正相关,0代表不相关,-1代表完美的负相关。
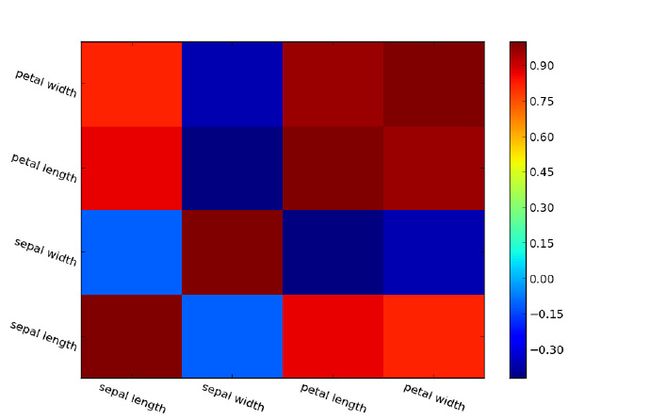
当变量数增长时我们可以使用伪彩色点很方便的可视化相关矩阵:
|
1
2
3
4
5
6
7
8
|
from
pylab
import
pcolor
,
colorbar
,
xticks
,
yticks
from
numpy
import
arrange
pcolor
(
corr
)
colorbar
(
)
# add
# arranging the names of the variables on the axis
xticks
(
arange
(
0.5
,
4.5
)
,
[
'sepal length'
,
'sepal width'
,
'petal length'
,
'petal width'
]
,
rotation
=
-
20
)
yticks
(
arange
(
0.5
,
4.5
)
,
[
'sepal length'
,
'sepal width'
,
'petal length'
,
'petal width'
]
,
rotation
=
-
20
)
show
(
)
|
看图右侧的彩条,我们可以把颜色点关联到数值上。在本例中,红色被关联为最高的正相关,我们可以看出我们数据集的最强相关是“花瓣宽度”和“花瓣长度”这两个变量。
第七章
降维
在第一章中我们了解了如何将鸢尾花数据集的两个维度可视化。单独使用该方法,我们只能看到数据集的部分数据视图。既然我们可以同时绘制的最高维度数为3,将整个数据集嵌入一系列维度并建立一个整体可视化视图是很有必要的。这个嵌入过程就被称作降维。最著名的降维技术之一就是主成分分析(PCA)。该技术把数据变量转换为等量或更少的不相关变量,称为主成分(PCs)。
这次,sklearn满足我们本次分析的所有需求:
|
1
2
|
from
sklearn
.
decomposition
import
PCA
pca
=
PCA
(
n_components
=
2
)
|
上述片段中我们实例化了一个PCA对象,用于计算前两个主成分。转换计算如下:
|
1
|
pcad
=
pca
.
fit_transform
(
data
)
|
然后如往常一样绘制结果:
|
1
2
3
4
|
plot
(
pcad
[
target
==
'setosa'
,
0
]
,
pcad
[
target
==
'setosa'
,
1
]
,
'bo'
)
plot
(
pcad
[
target
==
'versicolor'
,
0
]
,
pcad
[
target
==
'versicolor'
,
1
]
,
'ro'
)
plot
(
pcad
[
target
==
'virginica'
,
0
]
,
pcad
[
target
==
'virginica'
,
1
]
,
'go'
)
show
(
)
|
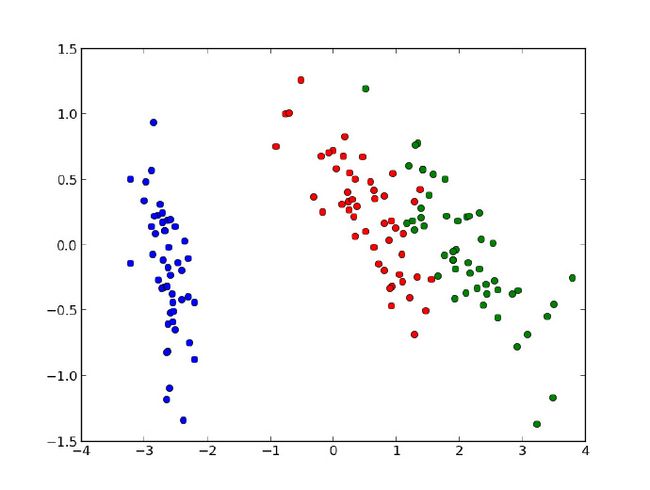
结果如下:
可以注意到上图和第一章提到的有些相似,不过这次变色鸢尾(红色的)和维吉尼亚鸢尾(绿色的)的间隔更清晰了。
PCA将空间数据方差最大化,我们可以通过方差比判断PCs包含的信息量:
|
1
2
|
print
pca
.
explained_variance_ratio
_
[
0.92461621
0.05301557
]
|
现在我们知道第一个PC占原始数据的92%的信息量而第二个占剩下的5%。我们还可以输出在转化过程中丢失的信息量:
|
1
2
|
print
1
-
sum
(
pca
.
explained_variance_ratio_
)
0.0223682249752
|
在本例中我们损失了2%的信息量。
此时,我们可以是应用逆变换还原原始数据:
|
1
|
data_inv
=
pca
.
inverse_transform
(
pcad
)
|
可以证明的是,由于信息丢失逆变换不能给出准确的原始数据。我们可以估算逆变换的结果和原始数据的相似度:
|
1
2
|
print
abs
(
sum
(
sum
(
data
-
data_inv
)
)
)
2.8421709430404007e
-
14
|
可以看出原始数据和逆变换计算出的近似值之间的差异接近于零。通过改变主成分的数值来计算我们能够覆盖多少信息量是很有趣的:
|
1
2
3
4
|
for
i
in
range
(
1
,
5
)
:
pca
=
PCA
(
n_components
=
i
)
pca
.
fit
(
data
)
print
sum
(
pca
.
explained_variance_ratio_
)
*
100
,
'%'
|
上述片段输出如下:
|
1
2
3
4
|
92.4616207174
%
97.7631775025
%
99.481691455
%
100.0
%
|
PCs用得越多,信息覆盖就越全,不过这段分析有助于我们理解保存一段特定的信息需要哪些组件。例如,从上述片段可以看出,只要使用三个PCs就可以覆盖鸢尾花数据集的几乎100%的信息。
第八章
网络挖掘
通常我们分析的数据是以网络结构存储的,例如我,我们的数据可以描述一群facebook用户的朋友关系或者科学家的论文的合作者关系。这些研究对象可以使用点和边描述之间的关系。
本章中我们将会介绍分析此类数据的基本步骤,称为图论,一个帮助我们创造、处理和研究网络的类库。尤其我们将会介绍如何使用特定方法建立有意义的数据可视化,以及如何建立一组关联稠密的点。
使用图论可以让我们很容易的导入用于描述数据结构的最常用结构:
|
1
|
G
=
nx
.
read_gml
(
'lesmiserables.gml'
,
relabel
=
True
)
|
在上述代码我们导入了《悲惨世界》同时出现的单词组成的网络,可以通过https://gephi.org/datasets/lesmiserables.gml.zip免费下载,数据以GML格式存储。我们还可以使用下面的命令导入并可视化网络:
|
1
|
nx
.
draw
(
G
,
node_size
=
0
,
edge_color
=
'b'
,
alpha
=
.
2
,
font_size
=
7
)
|
结果如下:
上图网络中每个点代表小说中的一个单词,两单词间的联系代表同一章里两单词同时出现了。很容易就发现这图不是很有帮助。该网络的大部分细节依然一藏着,并且发现很难发现那些重要点。我们可以研究节点度来获取一些内部细节。节点度是指一个最简中心测量并由一个点的多个关联组成。我们可以通过最大值、最小值、中位数、第一四分位数和第三四分位数来总结一个网络的度分布:
|
1
2
3
4
5
6
7
8
9
10
11
12
|
deg
=
nx
.
degree
(
G
)
from
numpy
import
percentile
,
mean
,
median
print
min
(
deg
.
values
(
)
)
print
percentile
(
deg
.
values
(
)
,
25
)
# computes the 1st quartile
print
median
(
deg
.
values
(
)
)
print
percentile
(
deg
.
values
(
)
,
75
)
# computes the 3rd quartile
print
max
(
deg
.
values
(
)
)
10
1
2.0
6.0
10.0
36
|
经过分析我们决定只考虑节点度大于10的点。我们可以建立一副只包含我们需要的点的新图来展现这些点:
|
1
2
3
4
5
6
|
Gt
=
G
.
copy
(
)
dn
=
nx
.
degree
(
Gt
)
for
n
in
Gt
.
nodes
(
)
:
if
dn
[
n
]
&
lt
;
=
10
:
Gt
.
remove_node
(
n
)
nx
.
draw
(
Gt
,
node_size
=
0
,
edge_color
=
'b'
,
alpha
=
.
2
,
font_size
=
12
)
|
结果见下图:
现在这幅图可读性大大提高了。这样我们就能观察到相关度最高的单词以及它们的关系。
通过识别团来研究网络也是很有趣的。团是指一个点和其他所有点相连的群组,极大团是指网络中不属于其它任何一个团的子集的团。我们可以通过如下方法发现我们网络中所有的极大团:
|
1
2
|
from
networkx
import
find_cliques
cliques
=
list
(
find_cliques
(
G
)
)
|
用下面这行命令输出极大团:
|
1
2
|
print
max
(
cliques
,
key
=
lambda
l
:
len
(
l
)
)
[
u
'Joly'
,
u
'Gavroche'
,
u
'Bahorel'
,
u
'Enjolras'
,
u
'Courfeyrac'
,
u
'Bossuet'
,
u
'Combeferre'
,
u
'Feuilly'
,
u
'Prouvaire'
,
u
'Grantaire'
]
|
我们可以看见列表中的绝大部分名字都和上图中可以看见的数据群中的相同。
第九章
其他资源
- IPython and IPython notebook,Python交互式脚本,也提供很棒的浏览器接口。[http://ipython.org/]
- NLTK,自然语言工具包,研究和开发自然语言处理的模块、数据和文档的套装。[http://nltk.org/]
- OpenCV,图像处理和计算机视觉的最重要的类库之一。[http://opencv.willowgarage.com/]
- Pandas, 为处理“关联的”或者“标签化的”数据提供最快、最自由、最富表现力的数据结构,使数据处理简单直接。[http://pandas.pydata.org/]
- Scipy,建立在numpy基础之上,提供大量的高等数据、信号处理、最优化和统计的算法和工具。[http://www.scipy.org/]
- Statsmodels, 大量的描述统计学、统计学检验、绘图函数,输出不同数据和不同统计的结果。[http://statsmodels.sourceforge.net/]
转载http://python.jobbole.com/83563/
未经作者同意转载,暂存,过几天删除。
大家可以移步伯乐在线查看,里面的python数据挖掘相关写的很好。