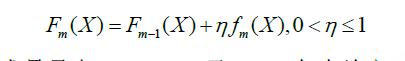xgboost原理详解

 本篇文章来自实习的时候我在小组里的一次xgboost分享。

 自己也是参考了很多资料加上自己的理解，如有错误的地方请各位大大指教，谢谢

基础

1、泰勒公式

 

2.、优化方法（梯度下降，牛顿法，拟牛顿等等）

 

3、回归树与GBDT

  

4、思想（GBDT的一种）：xgboost发展脉络整体认识和原理，自己的理解。更好的调参？

 

5、学习资料

回归（树回归+线性回归）+提升（boosting）+优化（5个方面）牛顿法、预排序、加权分位数、稀疏矩阵识别以及缓存识别等技术来大大提高了算法的性能

低维到高维的转变

 

极值点：

 

 

优化：（怎么求一个函数求极值？）

思想都是迭代法

 

各种各样的优化算法不同点在于：选取的步长不一样，选取的方向不一样。

 

Xgboost也是GBDT的一中，只不过进行了大量的优化！，其中一点就是优化方法选取了牛顿法（选取的方向不一样，一个梯度的方向，一个二阶导数的方向）

GBDT（梯度提升树）：

首先：

怎么构建迭代的回归提升树（CART），参考：

Cethik.vip/2016/09/21/machineCAST（或者统计学习方法书） 

简单讲就是：重复的构建很多树，每一颗树都是基于前面一棵树，使得当前这棵树拟合样本数据平方损失最小。

 

如果不是平方损失呢？

李航书：当损失函数是平方损失函数或者指数损失时，每一步优化很简单，但对一般损失函数，优化就不是那么容易了。于是，大神提出了梯度提升算法。

 

梯度提升算法本质：拟合一个回归树使得损失函数最小。

这个思想在优化算法经常用，没有解析解，就拟合一个近似值（比如著名的拟牛顿法），具体细节数学家研究的事情~~~~~~~~·

 

参数空间与函数空间：

因为梯度提升树就是在函数空间做优化

 

 

提升树用了Boosting思想

Boosting思想：先从初始训练集中训练出一个基学习器，再根据学习器的表现对训练样本分布进行调整，使得先前基学习器做错的样本在后续受到更多的关注，然后基于调整后的样本分布来训练下一个基学习器；如此重复进行，直到基学习器数目达到事先指定的T，最终将T个基学习器进行加权结合。

 

计算流程如下（梯度提升算法，优化算法）：

     类比梯度下降（所以叫梯度提升树嘛），一个参数空间，一个函数空间

      2.1  计算残差（计算值与真实之间的误差）

      2.2  拟合使得残差最小（当前学习的这棵树）

2.3  P 步长：基学习器的权重     H 树： 表示方向

      2.4  得到当前这一步的树

一句话总结：新模树的引入是为了减少上个树的残差(residual)，我们可以在残差减少的梯度(Gradient)方向上建立一个新的模型

 

对比提升树来说，提升树没有基学习器参权重ρ

   

随着T的增大我们的模型的训练误差会越来越小，如果无限迭代下去，理想情况下训练误差就会收敛到一个极小值，相应的会收敛到一个极小值点* P 。这是不是有种似曾相似的感觉，想一想在凸优化里面梯度下降法（参数空间的优化），是不是很像？我们就把F(x)看成是在N 维空间中的一个一个的点，而损失函数就是这个N 维空间中的一个函数（函数空间的优化），我们要用某种逐步逼近的算法来求解损失函数的极小值（最小值）。

题外话：

如果要将GBDT用于分类问题，怎么做呢？ 首先要明确的是，GBDT用于回归使用的仍然是CART回归树。回想我们做回归问题的时候，每次对残差（负梯度）进行拟合。而分类问题要怎么每次对残差拟合？要知道类别相减是没有意义的。因此，可以用Softmax进行概率的映射，然后拟合概率的残差！

具体的做法如下：

针对每个类别都先训练一个回归树，如三个类别，训练三棵树。就是比如对于样本xi为第二类，则输入三棵树分别为：(xi,0),(xi,1);(xi,0)这其实是典型的OneVsRest的多分类训练方式。 而每棵树的训练过程就是CART的训练过程。这样，对于样本xi就得出了三棵树的预测值F1(xi),F2(xi),F3(xi)，模仿多分类的逻辑回归，用Softmax来产生概率，以类别1为例：p1(xi)=exp(F1(xi))/∑3l=1exp(Fl(xi))

对每个类别分别计算残差，如

类别1：y~i1=0–p1(xi),

类别2： y~i2=1–p2(xi)，

 类别3：y~i3=0–p3(xi)

开始第二轮的训练，针对第一类 输入为(xi,y~i1), 针对第二类输入为(xi,y~i2) 针对第三类输入为 (xi,y~i3)，继续训练出三颗树。

重复3直到迭代M轮，就得到了最后的模型。预测的时候只要找出概率最高的即为对应的类别。

和上面的回归问题是大同小异的。

 

 

 

 

============================================================

 

 

XGBoost：

1，函数形式（模型长什么样）

2，目标\损失函数（学习的目标） 对模型参数进行修改

3. 学习策略（怎么样得到一个函数形式）

 

所有的机器学习的过程都是一个搜索假设空间的过程，我们的模型就是在空间中搜索一组参数（这组参数组成一个模型），使得和目标最接近（损失函数或目标函数最小），通过不断迭代的方式，不断的接近学习到真实的空间分布。

得到这样一个分布或者映射关系后，对空间里的未知样本或者新样本就可以做出预测/推理。这也解释了为什么一般样本越多模型效果越好，（大数定律）

有多少人工就有多少智能！

真实的样本空间是有噪声的，所以学习准确率不可能百分之百。（贝叶斯上限）

 

函数形式

       

目标函数

 

 

 

XGBOOST的目标函数

怎么求最小目标函数？

回顾：GBDT怎么做的，通过求一阶导数，迭代法的方式在函数空间拟合一个最小值。XGBOOST通过泰勒展开实现了更精确的拟合

对目标函数做泰勒展开

 

 

 

 

 

 

这个公式跟我们之前遇到的信息增益或基尼值增量的公式是一个道理。

XGBoost 就是利用这个公式计算出的值作为分裂条件

分裂后左边增益+右边增益-分类前增益

也就是“最大损失减小值”的原则来选择（是不是听名字就感觉很合理）

 

树节点分裂算法：

 

 

不会对该特征为missing的样本进行遍历统计，只对该列特征值为non-missing的样本上对应的特征值进行遍历

 

最后一步：

通过上述算法经过T此迭代我们得到T+1个弱学习器，{F(x)0,F(x)1,F(x)2..}.

那么通什么样的形式将他们迭代起来呢？答案是直接将T+1个模型相加，只不过为了防止过拟合，XGBoost也采用了shrinkage方法来降低过拟合的风险，其模型集成形式如下：

 

Shrinkage论文提到：关于n和迭代次数T 的取值，可以通过交叉验证得到合适的值，通常针对不同问题，其具体值是不同的。一般来说，当条条件允许时（如对模型训练时间没有要求等）可以设置一个较大的迭代次数T，然后针对该T 值利用交叉验证来确定一个合适的n值。但n的取值也不能太小，否则模型达不到较好的效果.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

更多特性

 

 

按照微软的官方说法：好像改进效果很明显。。。。。。

 

主要改进：直方图优化，进一步并行优化。

 

 

现在再看xgboost的参数意义与调优：

1）Booster:  分类器类型

2）lambda:  正则化

3）min_child_weight:子节点权重

4）树的深度

4）学习率n

···········

XGBoost总结：

1.损失函数是用泰勒展式二项逼近，而不是像GBDT里的就是一阶导数； 
2.对树的结构进行了正则化约束，防止模型过度复杂，降低了过拟合的可能性；

3.实现了并行化（树节点分裂的时候）

4.开头提到的优化

5.回归模型可选

参考资料：

统计学习方法

机器学习数学基础

从GBDT到xbgoost

Xbgoost原理解析

GBDT详解，火光摇曳

陈天奇论文

https://blog.csdn.net/qq_22238533/article/details/79192579