深度学习入门：AlphaGo Zero蒙特卡洛树搜索
先从《Mastering the Game of Go without Human Knowledge》说起，算法根据这篇论文来实现，AlphaZero只有几点不同而已。
总的来说，AlphaGo Zero分为两个部分，一部分是MCTS（蒙特卡洛树搜索），一部分是神经网络。
我们是要抛弃人类棋谱的，学会如何下棋完全是通过自对弈来完成。
过程是这样，首先生成棋谱，然后将棋谱作为输入训练神经网络，训练好的神经网络用来预测落子和胜率。如下图：
蒙特卡洛树搜索算法
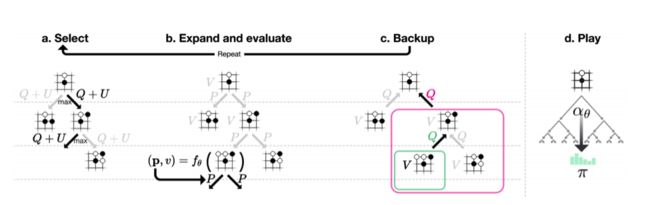
MCTS就是用来自对弈生成棋谱的，结合论文中的图示进行说明：
论文中的描述：
AlphaGo Zero中的蒙特卡洛树搜索。
- a.每次模拟通过选择具有最大行动价值Q的边加上取决于所存储的先验概率P和该边的访问计数N（每次访问都被增加一次）的上限置信区间U来遍历树。
- b.展开叶子节点，通过神经网络(P(s, ·), V (s)) = 来评估局面s；向量P的值存储在叶子结点扩展的边上。
- c.更新行动价值Q等于在该行动下的子树中的所有评估值V的均值。
- d.一旦MCTS搜索完成，返回局面s下的落子概率π，与N^(1 /τ)成正比，其中N是从根状态每次移动的访问计数， τ是控制温度的参数。
按照论文所述，每次MCTS使用1600次模拟。过程是这样的，现在AI从白板一块开始自己跟自己下棋，只知道规则，不知道套路，那只好乱下。每下一步棋，都要通过MCTS模拟1600次上图中的a~c，从而得出我这次要怎么走子。
来说说a~c，MCTS本质上是我们来维护一棵树，这棵树的每个节点保存了每一个局面（situation）该如何走子（action）的信息。这些信息是，N(s, a)是访问次数，W(s, a)是总行动价值，Q(s, a)是平均行动价值，P(s, a)是被选择的概率。
a. Select
每次模拟的过程都一样，从父节点的局面开始，选择一个走子。比如开局的时候，所有合法的走子都是可能的选择，那么我该选哪个走子呢？这就是select要做的事情。MCTS选择Q(s, a) + U(s, a)最大的那个action。Q的公式一会在Backup中描述。U的公式如下：
这个可以理解成：U(s, a) = c_puct × 概率P(s, a) × np.sqrt(父节点访问次数N) / ( 1 + 某子节点action的访问次数N(s, a) )
用论文中的话说，c_puct是一个决定探索水平的常数；这种搜索控制策略最初倾向于具有高先验概率和低访问次数的行为，但是渐近地倾向于具有高行动价值的行为。
计算过后，我就知道当前局面下，哪个action的Q+U值最大，那这个action走子之后的局面就是第二次模拟的当前局面。比如开局，Q+U最大的是当头炮，然后我就Select当头炮这个action，再下一次Select就从当头炮的这个棋局选择下一个走子。
b. Expand
现在开始第二次模拟了，假如之前的action是当头炮，我们要接着这个局面选择action，但是这个局面是个叶子节点。就是说当头炮之后可以选择哪些action不知道，这样就需要expand了，通过expand得到一系列可能的action节点。这样实际上就是在扩展这棵树，从只有根节点开始，一点一点的扩展。
Expand and evaluate这个部分有个需要关注的地方。论文中说：在队列中的局面由神经网络使用最小批量mini-batch 大小为8进行评估；搜索线程被锁定，直到评估完成。叶子节点被展开，每个边(s_L, a)被初始化为
然后值v被回传（backed up）。
如果我当前的局面没有被expand过，不知道下一步该怎么下，所以要expand，这个时候要用我们的神经网络出马。把当前的局面作为输入传给神经网络，神经网络会返回给我们一个action向量p和当前胜率v。其中action向量是当前局面每个合法action的走子概率。当然，因为神经网络还没有训练好，输出作为参考添加到我们的蒙特卡洛树上。这样在当前局面下，所有可走的action以及对应的概率p就都有了，每个新增的action节点都按照论文中说的对若干信息赋值， 。这些新增的节点作为当前局面节点的子节点。
c. Backup
接下来就是重点，evaluate和Backup一起说，先看看Backup做什么事吧：边的统计数据在每一步t≤L中反向更新。访问计数递增，
，并且动作价值更新为平均值， 
。我们使用虚拟损失来确保每个线程评估不同的节点。
我们来整理一下思路，任意一个局面（就是节点），要么被展开过（expand），要么没有展开过（就是叶子节点）。展开过的节点可以使用Select选择动作进入下一个局面，下一个局面仍然是这个过程，如果展开过还是可以通过Select进入下下个局面，这个过程一直持续下去直到这盘棋分出胜平负了，或者遇到某个局面没有被展开过为止。
如果没有展开过，那么执行expand操作，通过神经网络得到每个动作的概率和胜率v，把这些动作添加到树上，最后把胜率v回传（backed up），backed up给谁？
我们知道这其实是一路递归下去的过程，一直在Select，递归必须要有结束条件，不然就是死循环了。所以分出胜负和遇到叶子节点就是递归结束条件，把胜率v或者分出的胜平负value作为返回值，回传给上一层。
这个过程就是evaluate，是为了Backup步骤做准备。因为在Backup步骤，我们要用v来更新W和Q的，但是如果只做了一次Select，棋局还没有结束，此时的v是不明确的，必须要等到一盘棋完整的下完才能知道v到底是多少。就是说我现在下了一步棋，不管这步棋是好棋还是臭棋，只有下完整盘期分出胜负，才能给我下的这步棋评分。不管这步棋的得失，即使我这步棋丢了个车，但最后我赢了，那这个v就是积极的。同样即使我这步棋吃了对方一个子，但最后输棋了，也不能认为我这步棋就是好棋。
用一幅图概括一下这个过程：
当值被回传，就要做Backup了，这里很关键。因为我们是多线程同时在做MCTS，由于Select算法都一样，都是选择Q+U最大节点，所以很有可能所有的线程最终选择的是同一个节点，这就尴尬了。我们的目的是尽可能在树上搜索出各种不同的着法，最终选择一步好棋，怎么办呢？论文中已经给出了办法，“我们使用虚拟损失来确保每个线程评估不同的节点。”
就是说，通过Select选出某节点后，人为增大这个节点的访问次数N，并减少节点的总行动价值W，因为平均行动价值Q = W / N，这样分子减少，分母增加，就减少了Q值，这样递归进行的时候，此节点的Q+U不是最大，避免被选中，让其他的线程尝试选择别的节点进行树搜索。这个人为增加和减少的量就是虚拟损失virtual loss。
现在MCTS的过程越来越清晰了，Select选择节点，选择后，对当前节点使用虚拟损失，通过递归继续Select，直到分出胜负或Expand节点，得到返回值value。现在就可以使用value进行Backup了，但首先要还原W和N，之前N增加了虚拟损失，这次要减回去，之前减少了虚拟损失的W也要加回来。
然后开始做Backup，“边的统计数据在每一步t≤L中反向更新。访问计数递增，
，并且动作价值更新为平均值，
。”，这些不用我再解释了吧？同时我们还要更新U，U的公式上面给出过。这个反向更新，其实就是递归的把值返回回去。有一点一定要注意，就是我们的返回值一定要符号反转，怎么理解？就是说对于当前节点是胜，那么对于上一个节点一定是负，明白这个意思了吧？所以返回的是-value。
d. play
按照上述过程执行ac，论文中是每步棋执行1600次模拟，那就是1600次的ac，这个MCTS的过程就是模拟自我对弈的过程。模拟结束后，基本上能覆盖大多数的棋局和着法，每步棋该怎么下，下完以后胜率是多少，得到什么样的局面都能在树上找到。然后从树上选择当前局面应该下哪一步棋，这就是步骤d.play:“在搜索结束时，AlphaGo Zero在根节点s0选择一个走子a，与其访问计数幂指数成正比，
，其中τ是控制探索水平的温度参数。在随后的时间步重新使用搜索树：与所走子的动作对应的子节点成为新的根节点；保留这个节点下面的子树所有的统计信息，而树的其余部分被丢弃。如果根节点的价值和最好的子节点价值低于阈值v_resign，则AlphaGo Zero会认输。”
当模拟结束后，对于当前局面（就是树的根节点）的所有子节点就是每一步对应的action节点，选择哪一个action呢？按照论文所说是通过访问计数N来确定的。这个好理解吧？实现上也容易，当前节点的所有节点是可以获得的，每个子节点的信息N都可以获得，然后从多个action中选一个，这其实是多分类问题。我们使用softmax来得到选择某个action的概率，传给softmax的是每个action的logits（N(s_0,a)^(1/τ)）,这其实可以改成1/τ * log(N(s_0,a))。这样就得到了当前局面所有可选action的概率向量，最终选择概率最大的那个action作为要下的一步棋，并且将这个选择的节点作为树的根节点。
按照图1中a.Self-Play的说法就是，从局面进行自我对弈的树搜索（模拟），得到a_t∼ π_t，a_t就是动作action，π_t就是所有动作的概率向量。最终在局面s_T的时候得到胜平负的结果z，就是我们上面所说的value。
MCTS算法流程如下：
实现代码如下：
import numpy as np
import copy
def softmax(x):
probs = np.exp(x - np.max(x))
probs /= np.sum(probs)
return probs
class TreeNode(object):
"""A node in the MCTS tree.
Each node keeps track of its own value Q, prior probability P, and
its visit-count-adjusted prior score u.
"""
def __init__(self, parent, prior_p):
self._parent = parent
self._children = {} # a map from action to TreeNode
self._n_visits = 0
self._Q = 0
self._u = 0
self._P = prior_p
def expand(self, action_priors):
"""Expand tree by creating new children.
action_priors: a list of tuples of actions and their prior probability
according to the policy function.
"""
for action, prob in action_priors:
if action not in self._children:
self._children[action] = TreeNode(self, prob)
def select(self, c_puct):
"""Select action among children that gives maximum action value Q
plus bonus u(P).
Return: A tuple of (action, next_node)
"""
return max(self._children.items(),
key=lambda act_node: act_node[1].get_value(c_puct))
def update(self, leaf_value):
"""Update node values from leaf evaluation.
leaf_value: the value of subtree evaluation from the current player's
perspective.
"""
# Count visit.
self._n_visits += 1
# Update Q, a running average of values for all visits.
self._Q += 1.0*(leaf_value - self._Q) / self._n_visits
def update_recursive(self, leaf_value):
"""Like a call to update(), but applied recursively for all ancestors.
"""
# If it is not root, this node's parent should be updated first.
if self._parent:
self._parent.update_recursive(-leaf_value)
self.update(leaf_value)
def get_value(self, c_puct):
"""Calculate and return the value for this node.
It is a combination of leaf evaluations Q, and this node's prior
adjusted for its visit count, u.
c_puct: a number in (0, inf) controlling the relative impact of
value Q, and prior probability P, on this node's score.
"""
self._u = (c_puct * self._P *
np.sqrt(self._parent._n_visits) / (1 + self._n_visits))
return self._Q + self._u
def is_leaf(self):
"""Check if leaf node (i.e. no nodes below this have been expanded)."""
return self._children == {}
def is_root(self):
return self._parent is None
class MCTS(object):
"""An implementation of Monte Carlo Tree Search."""
def __init__(self, policy_value_fn, c_puct=5, n_playout=10000):
"""
policy_value_fn: a function that takes in a board state and outputs
a list of (action, probability) tuples and also a score in [-1, 1]
(i.e. the expected value of the end game score from the current
player's perspective) for the current player.
c_puct: a number in (0, inf) that controls how quickly exploration
converges to the maximum-value policy. A higher value means
relying on the prior more.
"""
self._root = TreeNode(None, 1.0)
self._policy = policy_value_fn
self._c_puct = c_puct
self._n_playout = n_playout
def _playout(self, state):
"""Run a single playout from the root to the leaf, getting a value at
the leaf and propagating it back through its parents.
State is modified in-place, so a copy must be provided.
"""
node = self._root
while(1):
if node.is_leaf():
break
# Greedily select next move.
action, node = node.select(self._c_puct)
state.do_move(action)
# Evaluate the leaf using a network which outputs a list of
# (action, probability) tuples p and also a score v in [-1, 1]
# for the current player.
action_probs, leaf_value = self._policy(state)
# Check for end of game.
end, winner = state.game_end()
if not end:
node.expand(action_probs)
else:
# for end state，return the "true" leaf_value
if winner == -1: # tie
leaf_value = 0.0
else:
leaf_value = (
1.0 if winner == state.get_current_player() else -1.0
)
# Update value and visit count of nodes in this traversal.
node.update_recursive(-leaf_value)
def get_move_probs(self, state, temp=1e-3):
"""Run all playouts sequentially and return the available actions and
their corresponding probabilities.
state: the current game state
temp: temperature parameter in (0, 1] controls the level of exploration
"""
for n in range(self._n_playout):
state_copy = copy.deepcopy(state)
self._playout(state_copy)
# calc the move probabilities based on visit counts at the root node
act_visits = [(act, node._n_visits)
for act, node in self._root._children.items()]
acts, visits = zip(*act_visits)
act_probs = softmax(1.0/temp * np.log(np.array(visits) + 1e-10))
return acts, act_probs
def update_with_move(self, last_move):
"""Step forward in the tree, keeping everything we already know
about the subtree.
"""
if last_move in self._root._children:
self._root = self._root._children[last_move]
self._root._parent = None
else:
self._root = TreeNode(None, 1.0)
def __str__(self):
return "MCTS"
class MCTSPlayer(object):
"""AI player based on MCTS"""
def __init__(self, policy_value_function,
c_puct=5, n_playout=2000, is_selfplay=0):
self.mcts = MCTS(policy_value_function, c_puct, n_playout)
self._is_selfplay = is_selfplay
def set_player_ind(self, p):
self.player = p
def reset_player(self):
self.mcts.update_with_move(-1)
def get_action(self, board, temp=1e-3, return_prob=0):
sensible_moves = board.availables
# the pi vector returned by MCTS as in the alphaGo Zero paper
move_probs = np.zeros(board.width*board.height)
if len(sensible_moves) > 0:
acts, probs = self.mcts.get_move_probs(board, temp)
move_probs[list(acts)] = probs
if self._is_selfplay:
# add Dirichlet Noise for exploration (needed for
# self-play training)
move = np.random.choice(
acts,
p=0.75*probs + 0.25*np.random.dirichlet(0.3*np.ones(len(probs)))
)
# update the root node and reuse the search tree
self.mcts.update_with_move(move)
else:
# with the default temp=1e-3, it is almost equivalent
# to choosing the move with the highest prob
move = np.random.choice(acts, p=probs)
# reset the root node
self.mcts.update_with_move(-1)
# location = board.move_to_location(move)
# print("AI move: %d,%d\n" % (location[0], location[1]))
if return_prob:
return move, move_probs
else:
return move
else:
print("WARNING: the board is full")
def __str__(self):
return "MCTS {}".format(self.player)
```
转自：[http://blog.csdn.net/chengcheng1394/article/details/79526474](http://blog.csdn.net/chengcheng1394/article/details/79526474)