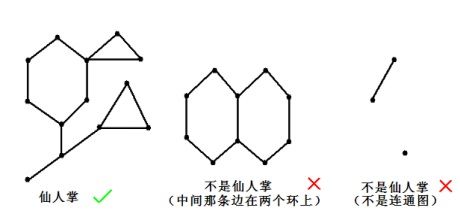
仙人掌
如果一个无自环无重边无向连通图的任意一条边最多属于一个简单环,我们就称之为仙人掌。所谓简单环即不经过重复的结点的环。
现在九条可怜手上有一张无自环无重边的无向连通图,但是她觉得这张图中的边数太少了,所以她想要在图上连上一些新的边。同时为了方便的存储这张无向图,图中的边数又不能太多。经过权衡,她想要加边后得到的图为一棵仙人掌。
不难发现合法的加边方案有很多,可怜想要知道总共有多少不同的加边方案。
两个加边方案是不同的当且仅当一个方案中存在一条另一个方案中没有的边。
\(\Sigma n\leq 5\times 10^5,m \leq 10^6\)。
wfj_2048的题解
注意到这题的仙人掌不允许重边,也就是环的大小至少为\(3\)。
首先特判掉一条边在超过一个环里的情况,只要判每个点到达根的路径是否大于\(2\)条就行了。(网上大多数人写特判掉不是仙人掌的情况,这是早就默认树是仙人掌了么?)
然后因为在环中的边已经不能被操作了,所以我们把环上的边拆掉,转化成了森林,然后做树形DP即可。单独考虑每棵树的答案,最后用乘法原理合并就好了。
然后就是对于每棵树统计答案了。
对于一个点\(x\),我们设\(f(x)\)表示\(x\)这棵子树连边形成仙人掌的方案数。我们发现,可以分为两种情况:
\(x\)这棵子树一定不与祖先连边,这个是根的情况。
\(x\)这棵子树可能与祖先连边,这个是除了根以外其他点的情况。
对于第1种情况,我们把\(x\)所有的儿子的\(f(y)\)都乘起来,并且我们计算一下\(x\)的儿子互相连边的情况,再乘起来就行了。
对于\(x\)的儿子互相连边的情况,我们可以找到一个规律。我们设\(g_i\)表示\(i\)个儿子互相连边的合法方案数,那么
\[ g_i=g_{i−1}+(i−1)g_{i−2} \]
这是怎么来的呢?我们考虑一下,如果第\(i\)个点不与其他点连边,那么方案数就是\(g_{i−1}\),否则,第\(i\)个点与第\(j\)个点连边,那么第\(j\)个点肯定不能与其他点连边,所以方案数是\(g_{i−2}\),总共有\(i−1\)种情况,所以\(g_i=g_{i−1}+(i−1)g_{i−2}\)。那么我们设\(x\)有\(tot\)个儿子,于是\(f(x)=\prod f(y) \times g_{tot}\)。
那么现在我们只要考虑第二种情况了。其实仔细想想,就是\(x\)的所有儿子\(f(y)\)相乘,再乘上\(g_{tot+1}\)就行了。因为算上父亲这就是\(tot+1\)个点互相连边的情况。于是\(f(x)=\prod f(y)\times g_{tot+1}\)。这个\(g_{tot+1}\)就考虑到了环的长度至少是\(3\)的条件,也就是DP基础了。
#include
#define co const
#define il inline
template T read(){
T x=0,w=1;char c=getchar();
for(;!isdigit(c);c=getchar())if(c=='-') w=-w;
for(;isdigit(c);c=getchar()) x=x*10+c-'0';
return x*w;
}
template il T read(T&x){
return x=read();
}
using namespace std;
typedef long long LL;
co int mod=998244353;
il int add(int a,int b){
return (a+=b)>=mod?a-mod:a;
}
il int mul(int a,int b){
return (LL)a*b%mod;
}
co int N=500000+10,M=1000000+10;
int n,m;
struct edge {int x,y;} eg[M];
vector to[N],enu[N];
int pos[N],low[N],dfn;
int st[N],top,col[N];
bool use[M],cact,vis[N];
int g[N],f[N];
void tarjan(int x,int fa){
bool cycl=0;
pos[x]=low[x]=++dfn,st[++top]=x;
for(int i=0;i<(int)to[x].size();++i){
int y=to[x][i];
if(y==fa) continue;
if(!pos[y]){
tarjan(y,x);
low[x]=min(low[x],low[y]);
if(low[y]();T--;) real_main();
return 0;
}