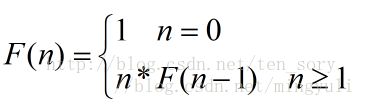递归(java)
一、递归方法(recursive method):一个直接或者间接调用自身的方法。即无限调用自身这个函数,每次调用总会改动一个关键变量,直到这个关键变量达到边界的时候,不再调用。
二、数学归纳法(induction):对于某个简单的情况定理是成立的,然后说明如何无限的扩展这个成立的范围。即如果对于最小的情况命题是成立的,而且可以从一种情况推导出下一种情况也成立,那么我们就知道该命题对于所有情况都是成立的。
数学函数可用递归定义。例如,设S(N)为前N个整数的和,则S(1)=1,S(N)可以写成S(N)=S(N-1)+N.此时用函数S本身的较小实例来定义函数S。
三、实例1
public class TestRecursive {
public static void main(String[] args) {System.out.println(s(4));
}
public static long s(int n){
if(n == 1)
return 1;
else
return s(n-1) + n;
}
}
程序中S看起来是调用自己,其实它是调用他自己的一个副本,这个副本是具有不同参数的另一个方法。在任何时刻只有一个副本是活动的,其他的都挂起。
基本情况是一个不用递归就可以解决的实例。任何递归调用要能最终结束都必须朝着这个情况请进。两个基本递归准则:
(1)、基本情况:至少有一个情况可以不用递归解决。
(2)、前进:任何递归调用都必须朝着基本情况前进。
程序出现的问题:如果参数 n很大,但还没有大到使答案超出int的范围,该程序仍会崩溃或者挂起。例如,我们的系统不能处理N>=8882的情况。原因:递归的实现需要记录一些调用过程以跟踪挂起的递归调用,对于朱够长的递归链,计算机就会用完内存。
四、实例2:求两个数的最大公约
比如说我现在要你用辗转相除法求出两个数的最大公约数,递归函数如下:
package com.lihe.test.collection;
public class TestGcd {
public static void main(String[] args) {
System.out.println(gcd(23,3));
}
public static int gcd(int a,int b){
return a%b==0?a:gcd(b,a%b);
}
辗转相除法基于如下原理:两个整数的最大公约数等于其中较小的数和两数的相除余数的最大公约数。
例如:a=25,b=15,a/b=10,b/10=15,10/5=20,最后一个为被除数余数的除数就是5,5就是所求最大公约数。
五、实例三:Fibonacci数
我们直到Fibonacci数的递推公式为:F(0)=F(1)=1,F(n)=F(n-1)+F(n-2) n>=2;
public class TestFibonacci {
public static void main(String[] args) {
System.out.println(Fibonacci(5));
}
public static int Fibonacci(int n){
if(n==0||n==1)
return 1;
return Fibonacci(n-1)+Fibonacci(n-2);
}
六、实例四:阶乘(factorial)
public class TestFactorial {
public static void main(String[] args) {
System.out.println(factorial(4));
}
public static int factorial(int n){
if(n==0)
return 1;
return n*factorial(n-1);
}
}
七、递归与循环的区别于联系
相同点:
(1)都是通过控制一个变量的边界(或者多个),来改变多个变量为了得到所需要的值,而反复而执行的;
(2)都是按照预先设计好的推断实现某一个值求取;(请注意,在这里循环要更注重过程,而递归偏结果一点)。
不同点:
(1)递归通常是逆向思维居多,“递”和“归”不一定容易发现(比较难以理解);而循环从开始条件到结束条件,包括中间循环变量,都需要表达出来(比较简洁明了)。
简单的来说就是:用循环能实现的,递归一般可以实现,但是能用递归实现的,循环不一定能。因为有些题目①只注重循环的结束条件和循环过程,而往往这个结束条件不易表达(也就是说用循环并不好写);②只注重循环的次数而不注重循环的开始条件和结束条件(这个循环更加无从下手了)。
八、求和实例解析
public class TestLeijia {
//先举个例子:定义一个 sumByMax(int max)方法,求 1+…+max 的和public static void main(String[] args) {
sumByMax1(10);
System.out.println(sumByMax2(10));
}
//非递归实现
public static void sumByMax1(int max){
int sum = 0;
while(max >= 1){//判断
sum += max;//累加
max --;//调整
}
System.out.println(sum);
}
//递归实现
public static int sumByMax2(int max){
if(max>=2){
return max+sumByMax2(max-1);
}else{
return max;
}
}
}
对于for或者while循环,只是将重复的步骤利用循环来处理,循环处理完一个步骤后,又进行下一个类似的步骤,关键点是要找出循环的依据和各步骤的相同点(既要循环的部分),什么情况下要继续循环,什么情况下要终止循环,如此例,从1到max有多少的整数就要循环多少次,这就是此例的循环依据,而此例中进行循环的重复操作是累加;
使用递归时,需先找出重复步骤之间的相同逻辑,然后将这些逻辑实现在一个方法中。
递归是在进行一个步骤,进行到某处时,通过调用自身进行分层,在下一层开始紧接着的下一个步骤, 如果下一层不是定义的最后一层,则会在相同的地方再次分层,直到进入最底层,如上例中,max如果 为5,在进行max为5的这一层操作时,将会运行addByMax(4),分层,下一层的max将为4,此时因为定义了max为1时 才为最底层,所以会继续分层,这时max为3,再分,为2,再分,为1,到达最底层,然后 从最底层开始将各层的结果一次向上传递,回归到最顶层,返回最终结果
所以递归时要注意形成一层一层的结构,一般会采取某种判断的方法,如if,如果不满足要求
,那就调用自身进行递归,此时应注意找出上下层之间的联系(各层相同逻辑的部分),让运算进入下一层,
这样形成上一层调用下一层,比如此例中的 max+addByMax(max-1)
最后注意定义一个最底层,即开始向上回归结果的那一层,最底层将不再调用自身进行递归。
以下是转载链接:https://www.jianshu.com/p/4db970d8ddc1
递归真是个奇妙的思维方式。自打我大二学习递归以来,对一些简单的递归问题,我总是惊叹于递归描述问题和编写代码的简洁。但是总感觉没能融会贯通地理解递归,有时尝试用大脑去深入“递归”,层次较深时便常产生进不去,出不来的感觉。这种状态也导致我很难灵活地运用递归解决问题。有一天,我看到一句英文:“To Iterate is Human, to Recurse, Divine.”中文译为:“人理解迭代,神理解递归。”然后,我心安理得地放弃了对递归的深入理解。直到看到王垠谈程序语言最精华的原理时提到了递归,并说递归比循环表达能力强很多,而且效率几乎一样。再次唤醒了我对递归的理解探索。
我首先在知乎上发现了下面两个例子,对比了递归和循环。例子来源于知乎用户李继刚的回答。
递归:你打开面前这扇门,看到屋里面还有一扇门(这门可能跟前面打开的门一样大小(静),也可能门小了些(动)),你走过去,发现手中的钥匙还可以打开它,你推开门,发现里面还有一扇门,你继续打开,。。。, 若干次之后,你打开面前一扇门,发现只有一间屋子,没有门了。 你开始原路返回,每走回一间屋子,你数一次,走到入口的时候,你可以回答出你到底用这钥匙开了几扇门。
循环:你打开面前这扇门,看到屋里面还有一扇门,(这门可能跟前面打开的门一样大小(静),也可能门小了些(动)),你走过去,发现手中的钥匙还可以打开它,你推开门,发现里面还有一扇门,(前面门如果一样,这门也是一样,第二扇门如果相比第一扇门变小了,这扇门也比第二扇门变小了(动静如一,要么没有变化,要么同样的变化)),你继续打开这扇门,。。。,一直这样走下去。 入口处的人始终等不到你回去告诉他答案。
该用户这么总结到:
递归就是有去(递去)有回(归来)。
**具体来说,为什么可以”有去“? **
这要求递归的问题需要是可以用同样的解题思路来回答除了规模大小不同其他完全一样的问题。
为什么可以”有回“?
这要求这些问题不断从大到小,从近及远的过程中,会有一个终点,一个临界点,一个baseline,一个你到了那个点就不用再往更小,更远的地方走下去的点,然后从那个点开始,原路返回到原点。
上面的解释几乎回答了我已久的疑问:为什么我老是有递归没有真的在解决问题的感觉?
因为递是描述问题,归是解决问题。而我的大脑容易被递占据,只往远方去了,连尽头都没走到,何谈回的来。
《漫谈递归:递归的思想》这篇文章将递归思想归纳为:
递归的基本思想是把规模大的问题转化为规模小的相似的子问题来解决。在函数实现时,因为解决大问题的方法和解决小问题的方法往往是同一个方法,所以就产生了函数调用它自身的情况。另外这个解决问题的函数必须有明显的结束条件,这样就不会产生无限递归的情况了。
需注意的是,规模大转化为规模小是核心思想,但递归并非是只做这步转化,而是把规模大的问题分解为规模小的子问题和可以在子问题解决的基础上剩余的可以自行解决的部分。而后者就是归的精髓所在,是在实际解决问题的过程。
我试图把我理解到递归思想用递归用程序表达出来,确定了三个要素:递 + 结束条件 + 归。
recursion(大规模)
{
if (end_condition)
{
end;
}
else
{ //先将问题全部描述展开,再由尽头“返回”依次解决每步中剩余部分的问题
recursion(小规模); //go;
solve; //back;
}
}
但是,我很容易发现这样描述遗漏了我经常会遇到的一种递归情况,比如递归遍历的二叉树的先序。我将这种情况用如下递归程序表达出来。
recursion(大规模)
{
if (end_condition)
{
end;
}
else
{ //在将问题转换为子问题描述的每一步,都解决该步中剩余部分的问题。
solve; //back;
recursion(小规模); //go;
}
}
总结到这里,我突然发现递归是为了最能表达这种思想,所以用“递归”这个词,其实递归可以是“有去有回”,也可以是“有去无回”。但其根本是“由大往小地去,由近及远地去”。“递”是必需,“归”并非必需,依赖于要解决的问题,有的需要去的路上解决,有的需要回来的路上解决。有递无归的递归其实就是我们很容易理解的一种分治思想。
其实理解递归可能没有“归”,只有去(分治)的情况后,我们应该想到递归也许可以既不需要在“去”的路上解决问题,也不需要在“归”的路上解决问题,只需在路的尽头解决问题,即在满足停止条件时解决问题。递归的分治思想不一定是要把问题规模递归到最小,还可以是将问题递归穷举其所有的情形,这时通常递归的表达力体现在将无法书写的嵌套循环(不确定数量的嵌套循环)通过递归表达出来。
将这种递归情形用递归程序描述如下:
recursion()
{
if (end_condition)
{
solve;
}
else
{ //在将问题转换为子问题描述的每一步,都解决该步中剩余部分的问题。
for () { recursion(); //go; }
}
}
例如,字符串的全排列就可以用这种递归简洁地表达出来,如下:
void permute(const string &prefix, const string &str)
{
if(str.length() == 0)
cout << prefix << endl;
else
{
for(int i = 0; i < str.length(); i++)
permute(prefix+str[i], str.substr(0,i)+str.substr(i+1,str.length()));
}
}
由这个例子,可以发现这种递归对递归函数参数出现了设计要求,即便递归到尽头,组合的字符串规模(长度)也没有变小,规模变小的是递归函数的一个参数。可见,这种变化似乎一下将递归的灵活性大大地扩展了,所谓的大规模转换为小规模需要有一个更为广义的理解了。
对递归的理解就暂时到这里了,可以看出文章中提到关于“打开一扇门”的递归例子来解释递归并不准确,例子只描述了递归的一种情况。而“递归就是有去(递去)有回(归来)”的论断同样不够准确。要为只读了文章前半部分的读者惋惜了。我也给出自己对递归思想的总结吧:
递归的基本思想是广义地把规模大的问题转化为规模小的相似的子问题或者相似的子问题集合来解决。广义针对规模的,规模的缩小具体可以是指递归函数的参数,也可以是其参数之一。相似是指解决大问题的方法和解决小问题的方法往往是同一个方法,还可以是指解决子问题集的各子问题的方法是同一个方法。解决大问题的方法可以是由解决次规模问题的方法和解决剩余部分的方法组成,也可以是由一系列解决次规模问题的方法组成。