Udacity机器学习入门笔记2-支持向量机(SVM)
Udacity机器学习入门笔记2-支持向量机(SVM)
- Udacity机器学习入门笔记2-支持向量机(SVM)
- 1.初步了解SVM
- 1.1 逻辑回归:logistic回归
- 1.2 线性分类的一个例子
- 1.3 函数间隔Functional margin与几何间隔Geometrical margin
- 1.4 最大间隔分类器Maximum Margin Classifier的定义
- 1.5 核函数
- 1.5.1 最简单的核函数
- 1.5.2 相似性函数
- 1.5.3 常用核函数
- 1.5.4 核函数的对比
- 1.5.5 核函数的选择
- 2.sklearn svm 学习
- 2.1 Classification
- 2.1.1 Multi-class classification
- 2.1.2 Scores and probabilities
- 2.1.3 Unbalanced problems
- 2.2 Regression
- 2.3 Density estimation, novelty detection
- 2.4 Complexity
- 2.5 Tips on Practical Use
- 2.6 kernel function
- 2.6.1 custom kernel
- 2.6.1.1 Using Python functions as kernels
- 2.6.1.2 Using the Gram matrix
- 2.6.1.3 Parameters of the RBF Kernel
- 3. Udacity mini-project
- 4. 参考文献
Udacity机器学习入门笔记2-支持向量机(SVM)
1.初步了解SVM
支持向量机,因其英文名为support vector machine,故一般简称SVM,通俗来讲,它是一种二类分类模型,其基本模型定义为特征空间上的间隔最大的线性分类器,其学习策略便是间隔最大化,最终可转化为一个凸二次规划问题的求解。
1.1 逻辑回归:logistic回归
理解SVM,咱们必须先弄清楚一个概念:线性分类器。
给定一些数据点,它们分别属于两个不同的类,现在要找到一个线性分类器把这些数据分成两类。如果用x表示数据点,用y表示类别(y可以取1或者-1,分别代表两个不同的类),一个线性分类器的学习目标便是要在n维的数据空间中找到一个超平面(hyper plane),这个超平面的方程可以表示为( w T w^T wT中的T代表转置):
w T x + b = 0 w^{T} x+b=0 wTx+b=0
可能有读者对类别取1或-1有疑问,事实上,这个1或-1的分类标准起源于logistic回归。
Logistic回归目的是从特征学习出一个0/1分类模型,而这个模型是将特性的线性组合作为自变量,由于自变量的取值范围是负无穷到正无穷。因此,使用logistic函数(或称作sigmoid函数)将自变量映射到(0,1)上,映射后的值被认为是属于y=1的概率。
假设函数 h θ ( x ) = g ( θ T x ) = 1 1 + e − θ T x h_{\theta}(x)=g\left(\theta^{T} x\right)=\frac{1}{1+e^{-\theta^{T} x}} hθ(x)=g(θTx)=1+e−θTx1
其中x是n维特征向量,函数g就是logistic函数。而 g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1的图像如下:

可以看到,将无穷映射到了(0,1)。
而假设函数就是特征属于y=1的概率。
P ( y = 1 ∣ x ; θ ) = h θ ( x ) P ( y = 0 ∣ x ; θ ) = 1 − h θ ( x ) \begin{array}{l}{P(y=1 | x ; \theta)=h_{\theta}(x)} \\ {P(y=0 | x ; \theta)=1-h_{\theta}(x)}\end{array} P(y=1∣x;θ)=hθ(x)P(y=0∣x;θ)=1−hθ(x)
从而,当我们要判别一个新来的特征属于哪个类时,只需求 h θ ( x ) h_{\theta}(x) hθ(x)即可,若 h θ ( x ) h_{\theta}(x) hθ(x)大于0.5就是y=1的类,反之属于y=0类。
此外,只 h θ ( x ) h_{\theta}(x) hθ(x)和 θ T x \theta^{T} x θTx有关, h θ ( x ) h_{\theta}(x) hθ(x)>0,那么,而g(z)只是用来映射,真实的类别决定权还是在于 θ T x \theta^{T} x θTx。再者,当 θ T x > > 0 \theta^{T} x>>0 θTx>>0时, h θ ( x ) h_{\theta}(x) hθ(x)=1,反之 h θ ( x ) h_{\theta}(x) hθ(x)=0。如果我们只从 θ T x \theta^{T} x θTx出发,希望模型达到的目标就是让训练数据中y=1的特征 θ T x > > 0 \theta^{T} x>>0 θTx>>0,而是y=0的特征 θ T x < < 0 \theta^{T} x<<0 θTx<<0。Logistic回归就是要学习得到 θ \theta θ,使得正例的特征远大于0,负例的特征远小于0,而且要在全部训练实例上达到这个目标。
接下来,尝试把logistic回归做个变形。首先,将使用的结果标签y = 0和y = 1替换为y = -1,y = 1,然后将 θ T x = θ 0 + θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n ( x 0 = 1 ) \theta^{T} x=\theta_{0}+\theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n} \quad\left(x_{0}=1\right) θTx=θ0+θ1x1+θ2x2+⋯+θnxn(x0=1)中的 θ 0 \theta_0 θ0替换为b,最后将后面的 θ 1 x 1 + θ 2 x 2 + ⋯ + θ n x n \theta_{1} x_{1}+\theta_{2} x_{2}+\cdots+\theta_{n} x_{n} θ1x1+θ2x2+⋯+θnxn替换为 w T x w^Tx wTx。如此,则有了 θ T x = w T x + b \theta^{T} x=w^{T} x+b θTx=wTx+b也就是说除了y由y=0变为y=-1外,线性分类函数跟logistic回归的形式化表示 h θ ( x ) = g ( θ T x ) = g ( w T x + b ) h_{\theta}(\mathrm{x})=g\left(\theta^{T} x\right)=\mathrm{g}\left(w^{T} x+\mathrm{b}\right) hθ(x)=g(θTx)=g(wTx+b)没区别。
进一步,可以将假设函数 h θ ( x ) = g ( w T x + b ) h_{\theta}(\mathrm{x})=\mathrm{g}\left(w^{T} x+\mathrm{b}\right) hθ(x)=g(wTx+b)中的g(z)做一个简化,将其简单映射到y=-1和y=1上。映射关系如下:
g ( z ) = { 1 , z ≥ 0 − 1 , z < 0 g(z)=\left\{\begin{aligned} 1, & z \geq 0 \\ -1, & z<0 \end{aligned}\right. g(z)={1,−1,z≥0z<0
1.2 线性分类的一个例子
下面举个简单的例子。如下图所示,现在有一个二维平面,平面上有两种不同的数据,分别用圈和叉表示。由于这些数据是线性可分的,所以可以用一条直线将这两类数据分开,这条直线就相当于一个超平面,超平面一边的数据点所对应的y全是-1 ,另一边所对应的y全是1。

这个超平面可以用分类函数 f ( x ) = w T x + b f(\mathrm{x})=w^{T} x+\mathrm{b} f(x)=wTx+b表示,当f(x) 等于0的时候,x便是位于超平面上的点,而f(x)大于0的点对应 y=1 的数据点,f(x)小于0的点对应y=-1的点,如下图所示:

换言之,在进行分类的时候,遇到一个新的数据点x,将x代入f(x) 中,如果f(x)小于0则将x的类别赋为-1,如果f(x)大于0则将x的类别赋为1。
接下来的问题是,如何确定这个超平面呢?从直观上而言,这个超平面应该是最适合分开两类数据的直线。而判定“最适合”的标准就是这条直线离直线两边的数据的间隔最大。所以,得寻找有着最大间隔的超平面。
1.3 函数间隔Functional margin与几何间隔Geometrical margin
在超平面wx+b=0确定的情况下,|wx+b|能够表示点x到距离超平面的远近,而通过观察wx+b的符号与类标记y的符号是否一致可判断分类是否正确,所以,可以用(y(w*x+b))的正负性来判定或表示分类的正确性。于此,我们便引出了函数间隔(functional margin)的概念。
定义函数间隔(用 γ ^ \hat{\gamma} γ^表示)为:
γ ^ = y ( w T x + b ) = y f ( x ) \hat{\gamma}=y\left(w^{T} x+b\right)=y f(x) γ^=y(wTx+b)=yf(x)
而超平面(w,b)关于T中所有样本点(xi,yi)的函数间隔最小值(其中,x是特征,y是结果标签,i表示第i个样本),便为超平面(w, b)关于训练数据集T的函数间隔:
γ ^ = min γ ^ i ( i = 1 , … n ) \hat{\gamma}=\min \hat{\gamma}_{\mathrm{i}(}\mathrm{i}=1, \ldots \mathrm{n}) γ^=minγ^i(i=1,…n)
但这样定义的函数间隔有问题,即如果成比例的改变w和b(如将它们改成2w和2b),则函数间隔的值f(x)却变成了原来的2倍(虽然此时超平面没有改变),所以只有函数间隔还远远不够。
事实上,我们可以对法向量w加些约束条件,从而引出真正定义点到超平面的距离–几何间隔(geometrical margin)的概念。
假定对于一个点 x ,令其垂直投影到超平面上的对应点为 x 0 x_0 x0 ,w 是垂直于超平面的一个向量, γ \gamma γ为样本x到超平面的距离,如下图所示:
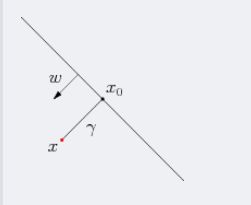
根据平面几何知识,有
x = x 0 + γ w ∥ w ∥ x=x_{0}+\gamma \frac{w}{\|w\|} x=x0+γ∥w∥w
其中||w||为w的二阶范数(范数是一个类似于模的表示长度的概念), w ∥ w ∥ \frac{w}{\|w\|} ∥w∥w是单位向量(一个向量除以它的模称之为单位向量)。
又由于 x 0 x_0 x0 是超平面上的点,满足 f( x 0 x_0 x0 )=0,代入超平面的方程 w T x 0 + b = 0 w^{T} x_0+b=0 wTx0+b=0,可得 w T x 0 = − b w^{T} x_{0}=-b wTx0=−b。
随即让此式 x = x 0 + γ w ∥ w ∥ x=x_{0}+\gamma \frac{w}{\|w\|} x=x0+γ∥w∥w的两边同时乘以 w T w^{T} wT,再根据 w T x 0 = − b w^{T} x_{0}=-b wTx0=−b和 w T w = ∥ w ∥ 2 w^{T} w=\|w\|^{2} wTw=∥w∥2,即可算出 γ \gamma γ:
γ = w T x + b ∥ w ∥ = f ( x ) ∥ w ∥ \gamma=\frac{w^{T} x+b}{\|w\|}=\frac{f(x)}{\|w\|} γ=∥w∥wTx+b=∥w∥f(x)
为了得到 γ \gamma γ的绝对值,令 γ \gamma γ乘上对应的类别 y,即可得出几何间隔(用 γ ~ \tilde{\gamma} γ~表示)的定义:
γ ~ = y γ = γ ^ ∥ w ∥ \tilde{\gamma}=y \gamma=\frac{\hat{\gamma}}{\|w\|} γ~=yγ=∥w∥γ^
从上述函数间隔和几何间隔的定义可以看出:几何间隔就是函数间隔除以||w||,而且函数间隔y*(wx+b) = y*f(x)实际上就是|f(x)|,只是人为定义的一个间隔度量,而几何间隔|f(x)|/||w||才是直观上的点到超平面的距离。
1.4 最大间隔分类器Maximum Margin Classifier的定义
对一个数据点进行分类,当超平面离数据点的“间隔”越大,分类的确信度(confidence)也越大。所以,为了使得分类的确信度尽量高,需要让所选择的超平面能够最大化这个“间隔”值。这个间隔就是下图中的Gap的一半。

通过由前面的分析可知:函数间隔不适合用来最大化间隔值,因为在超平面固定以后,可以等比例地缩放w的长度和b的值,这样可以使得 f ( x ) = w T x + b f(x)=w^{T} x+b f(x)=wTx+b的值任意大,亦即函数间隔 γ ^ \hat{\gamma} γ^可以在超平面保持不变的情况下被取得任意大。但几何间隔因为除上 ∥ w ∥ \|w\| ∥w∥了,使得在缩放w和b的时候几何间隔 γ ~ \tilde{\gamma} γ~的值是不会改变的,它只随着超平面的变动而变动,因此,这是更加合适的一个间隔。换言之,这里要找的最大间隔分类超平面中的“间隔”指的是几何间隔。
于是最大间隔分类器(maximum margin classifier)的目标函数可以定义为:
max γ ~ \max \tilde{\gamma} maxγ~
同时需满足一些条件,根据间隔的定义,有
y i ( w T x i + b ) = γ ^ i ≥ γ ^ , i = 1 , … , n y_{i}\left(w^{T} x_{i}+b\right)=\hat{\gamma}_{i} \geq \hat{\gamma}, \quad i=1, \ldots, n yi(wTxi+b)=γ^i≥γ^,i=1,…,n
其中,s.t.,即subject to的意思,它导出的是约束条件。
回顾下几何间隔的定义 γ ~ = y γ = γ ^ ∥ w ∥ \tilde{\gamma}=y \gamma=\frac{\hat{\gamma}}{\|w\|} γ~=yγ=∥w∥γ^,可知:如果令函数间隔 γ ^ \hat{\gamma} γ^等于1(之所以令等于1,是为了方便推导和优化,且这样做对目标函数的优化没有影响),则有 γ ~ \tilde{\gamma} γ~=1 / ||w||且 y i ( w T x i + b ) ≥ 1 , i = 1 , … , n y_{i}\left(w^{T} x_{i}+b\right) \geq 1, i=1, \dots, n yi(wTxi+b)≥1,i=1,…,n,从而上述目标函数转化成了
max 1 ∥ w ∥ , s . t . , y i ( w T x i + b ) ≥ 1 , i = 1 , … , n \max \frac{1}{\|w\|}, \quad s . t ., y_{i}\left(w^{T} x_{i}+b\right) \geq 1, i=1, \ldots, n max∥w∥1,s.t.,yi(wTxi+b)≥1,i=1,…,n
相当于在相应的约束条件下 y i ( w T x i + b ) ≥ 1 , i = 1 , … , n y_{i}\left(w^{T} x_{i}+b\right) \geq 1, i=1, \dots, n yi(wTxi+b)≥1,i=1,…,n,最大化这个1/||w||值,而1/||w||便是几何间隔 γ ~ \tilde{\gamma} γ~。
如下图所示,中间的实线便是寻找到的最优超平面(Optimal Hyper Plane),其到两条虚线边界的距离相等,这个距离便是几何间隔 γ ~ \tilde{\gamma} γ~,两条虚线间隔边界之间的距离等于 2 γ ~ 2\tilde{\gamma} 2γ~,而虚线间隔边界上的点则是支持向量。由于这些支持向量刚好在虚线间隔边界上,所以它们满足(还记得我们把 functional margin 定为 1 了吗?上节中:处于方便推导和优化的目的,我们可以令 γ ^ \hat{\gamma} γ^=1),而对于所有不是支持向量的点,则显然有 y ( w T x + b ) > 1 y\left(w^{T} x+b\right)>1 y(wTx+b)>1。

1.5 核函数
核函数是特征转换函数。
1.5.1 最简单的核函数
回顾上面内容,我们的任务是找出合适的参数w,b,使得分割超平面间距最大,且能正确对数据进行分类。间距最大是我们的优化目标。真确地对数据分类是约束条件。即在满足约束条件 y ( i ) ( w T x ( i ) + b ) ≥ 1 y^{(i)}\left(w^{T} x^{(i)}+b\right) \geq 1 y(i)(wTx(i)+b)≥1的前提下,求解 ∣ ∣ w ∣ ∣ 2 ||w||^2 ∣∣w∣∣2的最小值。
拉格朗日乘子法是解决约束条件下求函数极值的理想方法。其方法是引入非负系数α来作为约束条件的权重:
L = 1 2 ∥ w ∥ 2 − ∑ i = 1 m α i ( y ( i ) ( w T x ( i ) + b ) − 1 ) L=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{m} \alpha_{i}\left(y^{(i)}\left(w^{T} x^{(i)}+b\right)-1\right) L=21∥w∥2−i=1∑mαi(y(i)(wTx(i)+b)−1)
由于极值的偏导数为0,因此这需要让L对w求导使之为0得到w和α对关系:
w = ∑ i = 1 m α i y ( i ) x ( i ) w=\sum_{i=1}^{m} \alpha_{i} y^{(i)} x^{(i)} w=i=1∑mαiy(i)x(i)
接着继续求L对b对偏导数得出:
∑ i = 1 m y ( i ) α i = 0 \sum_{i=1}^{m} y^{(i)} \alpha_{i}=0 i=1∑my(i)αi=0
把这两个式子代入L通过数学运算得出(推导公式有所省略):
L = ∑ i = 1 m α i − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y ( i ) y ( j ) x ( i ) T x ( j ) L=\sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y^{(i)} y^{(j)} x^{(i) T} x^{(j)} L=i=1∑mαi−21i=1∑mj=1∑mαiαjy(i)y(j)x(i)Tx(j)
这个公式中m是数据集个数, α \alpha α是拉格朗日乘子法引入的一个系数,针对数据集中的每个样本 x ( i ) x^{(i)} x(i),都有对应的 α i \alpha_i αi。 x ( i ) x^{(i)} x(i)是数据集中地i个样本的输入,它是一个向量, y ( i ) y^{(i)} y(i)是对应的输出标签,值为 y ∈ [ − 1 , 1 ] y \in[ -1,1] y∈[−1,1]。
这个公式的最小值求解这里就不说明了。最后求出的a有个明显的特点。即大部分 α i \alpha_i αi=0。因为只有那些支持向量所对应的样本直接决定了间隙的大小。实际上以上推导出这个公式就是为了引入支持向量机的另外一个核心概念:核函数:
K ( x ( i ) , x ( j ) ) = x ( i ) T x ( j ) K\left(x^{(i)}, x^{(j)}\right)=x^{(i) T} x^{(j)} K(x(i),x(j))=x(i)Tx(j)
L里的 x ( i ) T x ( j ) x^{(i) T} x^{(j)} x(i)Tx(j)部分,其中 x ( i ) x^{(i)} x(i)是一个特征向量,所以 x ( i ) T x ( j ) x^{(i) T} x^{(j)} x(i)Tx(j)是一个数值,就是两个输入特征向量的内积。预测函数为:
w T x + b = ∑ i = 1 m α i y ( i ) x ( i ) T x + b w^{T} x+b=\sum_{i=1}^{m} \alpha_{i} y^{(i)} x^{(i) T} x+b wTx+b=i=1∑mαiy(i)x(i)Tx+b
当 w T x + b > 0 w^{T} x+b>0 wTx+b>0,预测函数为类别1,当 w T x + b < 0 w^{T} x+b<0 wTx+b<0,预测类别为-1。注意到预测函数里也包含式子 x ( i ) T x x^{(i)T}x x(i)Tx。我们把 K ( x ( i ) , x ( j ) ) = x ( i ) T x ( j ) K\left(x^{(i)}, x^{(j)}\right)=x^{(i) T} x^{(j)} K(x(i),x(j))=x(i)Tx(j)称为核函数。 x ( i ) T x ( j ) x^{(i) T} x^{(j)} x(i)Tx(j)是两个向量内积,它的物理含义是衡量两个向量的相似性。典型地,当两个向量相互垂直是,即完全线性无关,此时 x ( i ) T x ( j ) = 0 x^{(i) T} x^{(j)}=0 x(i)Tx(j)=0。引入核函数后预测函数为:
w T x + b = ∑ i = 1 m α i y ( i ) K ( x ( i ) , x ) + b w^{T} x+b=\sum_{i=1}^{m} \alpha_{i} y^{(i)} K\left(x^{(i)}, x\right)+b wTx+b=i=1∑mαiy(i)K(x(i),x)+b
1.5.2 相似性函数
解决这个问题的方式是:用一定规则把这些无法进行线性分割的样本映射到更高纬度的空间里,然后找出超平面。
SVM的核函数就是为了实现这种相似性映射。最简单的核函数是 K ( x ( i ) , x ( j ) ) = x ( i ) T x ( j ) K\left(x^{(i)}, x^{(j)}\right)=x^{(i) T} x^{(j)} K(x(i),x(j))=x(i)Tx(j)
,它衡量的是两个输入特征向量的相似性。可以通过定义和函数 K ( x ( i ) , x ( j ) ) K\left(x^{(i)}, x^{(j)}\right) K(x(i),x(j))
来重新定义相似性,从而得到想要的映射。例如在基因测试领域,我们需要根据DNA分子的特征来定义相似性函数,即和函数。在文本处理领域,也可以自己定义和函数来衡量两个词之间的相似性。
怎么把低维度的空间映射到高纬度的空间呢?
举个例子:联想下利用多项式解决线性回归欠拟合问题的方法。如果输入特征是一维的[x1]
变量,我们把它变成二维的一个方法是把输入特征转化为 [ x 1 , 2 x 1 2 ] [x_1,2x_1^2] [x1,2x12],定义这种特征映射的函数就称之为相似性函数Φ(x)。这样在原来低维度计算相似性的运算 x ( i ) T x ( j ) x^{(i) T} x^{(j)} x(i)Tx(j),就可以转换为高纬度空间里进行相似性运算 Φ ( x ( i ) ) T Φ ( x ( i ) ) \Phi\left(x^{(i)}\right)^{T} \Phi\left(x^{(i)}\right) Φ(x(i))TΦ(x(i))。
核函数 K ( x ( i ) , x ( j ) ) K\left(x^{(i)}, x^{(j)}\right) K(x(i),x(j))和相似性函数Φ(x)的关系:
相似性函数是特征的映射函数,起到转换的作用。而核函数是特征向量的内积。经过相似性函数转换后,核函数变成 K ( x ( i ) , x ( j ) ) = Φ ( x ( i ) ) T Φ ( x ( i ) ) K\left(x^{(i)}, x^{(j)}\right)=\Phi\left(x^{(i)}\right)^{T} \Phi\left(x^{(i)}\right) K(x(i),x(j))=Φ(x(i))TΦ(x(i))。
1.5.3 常用核函数
核函数一般和应用场景相关,在不同领域所应用的核函数可能也不相同。但是实际上也有一些通用核函数“万金油”,一般有两种:多项式核函数和高斯核函数。
1、多项式核函数:
K ( x ( i ) , x ( j ) ) = ( γ x ( i ) T x ( j ) + c ) n K\left(x^{(i)}, x^{(j)}\right)=\left(\gamma x^{(i) T} x^{(j)}+c\right)^{n} K(x(i),x(j))=(γx(i)Tx(j)+c)n
2、高斯核函数:
K ( x ( i ) , x ( j ) ) = exp ( − ( x ( i ) − x ( j ) ) 2 2 σ 2 ) K\left(x^{(i)}, x^{(j)}\right)=\exp \left(-\frac{\left(x^{(i)}-x^{(j)}\right)^{2}}{2 \sigma^{2}}\right) K(x(i),x(j))=exp(−2σ2(x(i)−x(j))2)
如果输入的特征是一维的标量,那么高斯核函数对应的形状就是一个反钟形的曲线,其参数σ控制反钟形的宽度。如下图所示:
 由于 K ( x ( i ) , x ( j ) ) = Φ ( x ( i ) ) T Φ ( x ( i ) ) K\left(x^{(i)}, x^{(j)}\right)=\Phi\left(x^{(i)}\right)^{T} \Phi\left(x^{(i)}\right) K(x(i),x(j))=Φ(x(i))TΦ(x(i))经过合适的数学变换,可得高斯核函数对应的特征转换函数为:
由于 K ( x ( i ) , x ( j ) ) = Φ ( x ( i ) ) T Φ ( x ( i ) ) K\left(x^{(i)}, x^{(j)}\right)=\Phi\left(x^{(i)}\right)^{T} \Phi\left(x^{(i)}\right) K(x(i),x(j))=Φ(x(i))TΦ(x(i))经过合适的数学变换,可得高斯核函数对应的特征转换函数为:
Φ ( x ) = ∑ i = 0 ∞ exp ( − x 2 ) 2 i i ! x i \Phi(x)=\sum_{i=0}^{\infty} \exp \left(-x^{2}\right) \sqrt{\frac{2^{i}}{i !}} x^{i} Φ(x)=i=0∑∞exp(−x2)i!2ixi
前面无限多项的累加器,其物理意义就是把特征向量转换到无限多维向量空间里,即高斯函数可以吧输入特征扩展到无限多维空间里。公式的推导公式会用到泰勒公式。
高 斯 预 测 函 数 = ∑ i = 1 m a i y ( i ) K ( x ( i ) , x ) + b 高斯预测函数=\sum_{i=1}^{m} a_{i} y^{(i)} K\left(x^{(i)}, x\right)+b 高斯预测函数=i=1∑maiy(i)K(x(i),x)+b
其中 K ( x ( i ) , x ( j ) ) K\left(x^{(i)}, x^{(j)}\right) K(x(i),x(j))是高斯核函数, a i a_i ai只在支持向量对应的样本出不为0.由此可知,预测函数时中心点在支持向量机处的高斯函数的线性组合,其线性组合的系数为 a i y ( i ) a_iy^{(i)} aiy(i)。因此,高斯核函数也称为RBF核函数,即反钟形函数的线性组合。
1.5.4 核函数的对比
1、线性核函数:这是最简单的核函数,它直接计算两个输入特征向量的内积。
K ( x ( i ) , x ( j ) ) = x ( i ) T x ( j ) K\left(x^{(i)}, x^{(j)}\right)=x^{(i) T} x^{(j)} K(x(i),x(j))=x(i)Tx(j)
优点:简单高效,结果易解释,总能生成一个最简洁的线性分割超平面
缺点:只适用线性可分的数据集
2、多项式核函数:通过多项式来作为特征映射函数
K ( x ( i ) , x ( j ) ) = ( γ x ( i ) T x ( j ) + c ) n K\left(x^{(i)}, x^{(j)}\right)=\left(\gamma x^{(i) T} x^{(j)}+c\right)^{n} K(x(i),x(j))=(γx(i)Tx(j)+c)n
优点:可以拟合出复杂的分割超平面。
缺点:参数太多。有γ,c,n
三个参数要选择,选择起来比较困难;另外多项式的阶数不宜太高否则会给模型求解带来困难。
3、高斯核函数:
K ( x ( i ) , x ( j ) ) = exp ( − ( x ( i ) − x ( j ) ) 2 2 σ 2 ) K\left(x^{(i)}, x^{(j)}\right)=\exp \left(-\frac{\left(x^{(i)}-x^{(j)}\right)^{2}}{2 \sigma^{2}}\right) K(x(i),x(j))=exp(−2σ2(x(i)−x(j))2)
优点:可以把特征映射到无限多维,并且没有多项式计算那么困难,参数也比较好选择。
缺点:不容易解释,计算速度比较慢,容易过拟合。
1.5.5 核函数的选择
1、最一般的选择原则是针对数据量很大的时候,可以选择复杂一点的模型。虽然复杂模型容易过拟合,但由于数据量很大,可以有效弥补过拟合问题。如果数据集较小选择简单点的模型,否则很容易过拟合,此时特别要注意模型是否欠拟合,如果欠拟合可以增加多项式纠正欠拟合。
2、根据样本量m和特征量n
进行选择:
特征相比样本较大(如m=10~1000,n=10000):选逻辑回归或者线性函数SVM
特征较少,样本量中(如m=10~10000,n=1~1000):选择高斯SVM
特征量少,样本多(如m=50000+,n=1~1000):选多项式或高斯SVM
2.sklearn svm 学习
支持向量机(SVM)是一组用于监督学习方法分类, 回归和异常值的检测。
支持向量机的优点是:
- 在高维空间有效。
- 当维数大于样品的数量时,仍然有效。
- 在决策函数中使用训练数据(称为支持向量)的一个子集,所以它内存使用也是有效率。
- 通用性:可以为不同决策功能指定不同的内核函数。提供了常见的内核,但它也可以指定自定义内核。
支持向量机的缺点包括:
- 如果特征的数量比样本的数量大得多,避免过度拟合在选择内核函数和调整项是至关重要的。
- 支持向量机不直接提供的概率估计,这些使用昂贵的5倍交叉验证(见计算得分和概率,下文)。
在支持向量机scikit学习支持稠密(numpy.ndarray和通过转换为该numpy.asarray)和稀疏(任何scipy.sparse)取样矢量作为输入。但是,要使用SVM进行稀疏数据预测,它一定是已经使用这些数据进行训练。为了获得最佳性能,使用C-ordered numpy.ndarray(稠密)或 scipy.sparse.csr_matrix(稀疏)用dtype=float64。
2.1 Classification
SVC,NuSVC和LinearSVC能够在数据集上执行多类分类的类。

SVC和NuSVC类似的方法,但接受稍有不同的参数集,并具有不同的数学公式。在另一方面,LinearSVC是一个线性核的情况下,支持向量分类的另一种实现方式。请注意, LinearSVC不接受关键字kernel,因为这被认为是线性的。它还缺少一些成员 SVC和NuSVC一样support_。
作为其它分类器,SVC,NuSVC和 LinearSVC输入是两个数组:一个存训练数据,另一个存标签
>>> from sklearn import svm
>>> X = [[0, 0], [1, 1]]
>>> y = [0, 1]
>>> clf = svm.SVC(gamma='scale')
>>> clf.fit(X, y)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='scale', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
训练后,该模型可以被用来预测新的价值
>>> clf.predict([[2., 2.]])
array([1])
支持向量机决策函数依赖于训练数据的某个子集,称为支持向量。这些支持向量的某些属性可以在成员变量support_vectors_,support_和 n_support中找到:
>>> # get support vectors
>>> clf.support_vectors_
array([[0., 0.],
[1., 1.]])
>>> # get indices of support vectors
>>> clf.support_
array([0, 1]...)
>>> # get number of support vectors for each class
>>> clf.n_support_
array([1, 1]...)
2.1.1 Multi-class classification
SVC和NuSVC实施“一对一”的方法(Knerr等人,1990)用于多类分类。如果 n_class是的类的数量,则 n_class * (n_class - 1) / 2分类器被构造和每一个从两个类训练数据。为了提供与其他分类一致的界面,该 decision_function_shape选项允许聚集“一对一”分类器形状的决策函数的结果:decision_function_shape(n_samples, n_classes)
>>> X = [[0], [1], [2], [3]]
>>> Y = [0, 1, 2, 3]
>>> clf = svm.SVC(gamma='scale', decision_function_shape='ovo')
>>> clf.fit(X, Y)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovo', degree=3, gamma='scale', kernel='rbf',
max_iter=-1, probability=False, random_state=None, shrinking=True,
tol=0.001, verbose=False)
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes: 4*3/2 = 6
6
>>> clf.decision_function_shape = "ovr"
>>> dec = clf.decision_function([[1]])
>>> dec.shape[1] # 4 classes
4
在另一方面,LinearSVC实行“one-vs-the-rest”多类策略,从而培养n_class模型。如果只有两类,只有一种模式进行训练:
>>> lin_clf = svm.LinearSVC()
>>> lin_clf.fit(X, Y)
LinearSVC(C=1.0, class_weight=None, dual=True, fit_intercept=True,
intercept_scaling=1, loss='squared_hinge', max_iter=1000,
multi_class='ovr', penalty='l2', random_state=None, tol=0.0001,
verbose=0)
>>> dec = lin_clf.decision_function([[1]])
>>> dec.shape[1]
4
LinearSVC提供了另一种多分类策略,即是所谓的多类SVM,由Crammer和Singer设计的,它的实现通过选项multi_class=‘crammer_singer’ 完成。这个方法是一致性的,而 one-vs-rest 分类不是。在实际应用中更喜欢用 one-vs-rest分类,因为效果类似但运行更快。
对于“one-vs-rest” LinearSVC,它的属性 coef_ 和 intercept_的数据类型分别为[n_class, n_features] 和 [n_class],参数coef_的每一行对应一个 “one-vs-rest”的分类器,与intercept_一样,以类的顺序排列。
对于“one-vs-one” SVC,他的属性的布局比较困难。以线性核为例,他的属性coef_ 和 intercept_的数据类型分别是[n_class * (n_class - 1) / 2, n_features] 和 [n_class * (n_class - 1) / 2]。跟之前的LinearSVC类似,每一行对应的是一个二元分类器,类的排序从0到n是“0 vs 1”, “0 vs 2” , … “0 vs n”, “1 vs 2”, “1 vs 3”, “1 vs n”, . . . “n-1 vs n”。
dual_coef_数据类型[n_class-1, n_SV],有点难以把握理解,列对应的是 “one-vs-one” 分类器中涉及到的支持向量。每一个向量会在n_class - 1个分类器中用到,各行中的 n_class - 1 各项对应的是这些分类其双元系数。
这可以用一个例子来更加明确:
假设一个3分类问题,类0有三个支持向量 v 0 0 , v 0 1 , v 0 2 v_{0}^{0}, v_{0}^{1}, v_{0}^{2} v00,v01,v02,类1和类2分别有两个支持向量 v 1 0 , v 1 1 v_{1}^{0}, v_{1}^{1} v10,v11和 v 2 0 , v 2 1 v_{2}^{0}, v_{2}^{1} v20,v21。对于每一个向量 v i j v_{i}^{j} vij,都有两个双元系统,分别是类别 i i i 和 k α i , k j k\alpha_{i,k}^j kαi,kj。 dual_coef_看起来如下图:

2.1.2 Scores and probabilities
所述decision_function的方法SVC和NuSVC给出了每个类为每个样品的分数(或在二分类的情况下,每个样品的单个分数)。当构造选项probability设置为True,类别成员概率估计(从方法predict_proba和 predict_log_proba)被启用。在二分类的情况下,概率使用普拉特缩放校准:对SVM的分数逻辑回归,通过对训练数据的额外交叉验证实现:。在多分类情况下,方法如在Wu et al. (2004)扩展的一样。
不用说,对大型数据集进行普拉特缩放交叉验证是昂贵的操作。此外,概率估计可能是跟分数不一致的,在这个意义上,该分数的“argmax”可能不是概率的argmax。(例如,在二元分类,一个标记predict的样品可能属于由predict_proba获得概率<½的一个类。)普氏方法具有理论问题。如果需要的置信度,但是这些不必是概率,那么最好是设置probability=False 和使用decision_function代替predict_proba。
2.1.3 Unbalanced problems
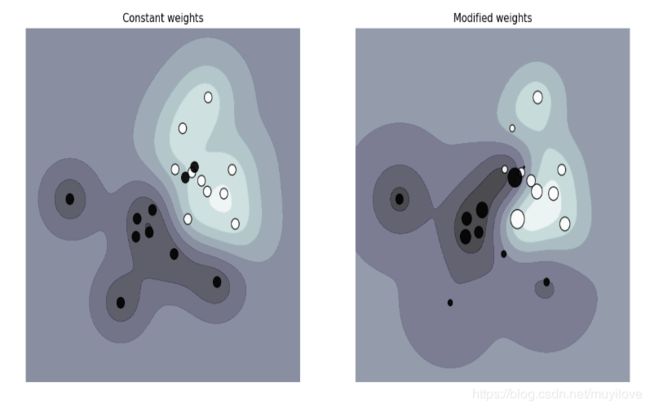
在其中期望给予某些类或某些个别样品更大的权重,关键字class_weight和 sample_weight可以使用。
SVC(不是NuSVC)在fit方法中执行关键字 class_weight。它以字典形式 {class_label : value},其中值是大于0的浮点数,则设置class_label类的参数C为C * value.

SVC,NuSVC,SVR,NuSVR和 OneClassSVM也在 fit方法中通过关键字sample_weight改变个体样本的权重。类似class_weight,设置第 i i i个样本的参数C为C * sample_weight[i]。
2.2 Regression
支持向量分类的方法可以扩展到解决回归问题。这个方法被称为Support Vector Regression。
支持向量分类所产生的模型只依赖训练数据的一个子集,只是因为用于建立模型的代价函数只关心边缘附近的训练数据。类似的,支持向量回归也是依赖于训练数据的一个子集,原因是他会忽略预测模型附近的训练数据。
总共有3个支持向量回归的工具,SVR, NuSVR 和 LinearSVR。LineaSVR提供了比SVR更快的实现方法,但是只考虑线性核,同时NuSVR跟SVR和LinearSVR实现的数学模型有些不同。
跟分类方法一样,fit 方法以向量X为输入,y在这里的数据类型是浮点数,而不是分类中的整型。
>>> from sklearn import svm
>>> X = [[0, 0], [2, 2]]
>>> y = [0.5, 2.5]
>>> clf = svm.SVR()
>>> clf.fit(X, y)
SVR(C=1.0, cache_size=200, coef0=0.0, degree=3, epsilon=0.1,
gamma='auto_deprecated', kernel='rbf', max_iter=-1, shrinking=True,
tol=0.001, verbose=False)
>>> clf.predict([[1, 1]])
array([1.5])
2.3 Density estimation, novelty detection
oneClassSVM 类实现了单类的SVM, 主要用于异常值检测。
2.4 Complexity
支持向量机是强大的工具,但他们的计算和存储需求与培训向量的数量迅速增加。一个SVM的核心是一个二次规划问题(QP),从训练数据的其余部分分离支持向量。基于libsvm的QP求解器的使用规模在与 O ( n features × n samples 2 ) O\left(n_{\text {features}} \times n_{\text {samples}}^{2}\right) O(nfeatures×nsamples2)和 O ( n features × n samples 3 ) O\left(n_{\text {features}} \times n_{\text {samples}}^{3}\right) O(nfeatures×nsamples3)之间,具体取决于 libsvm 缓存的使用效率。如果数据集是非常稀疏的, n features n_{\text { features }} n features 应该由样本矢量的非零特征的平均数量来代替。
另外请注意,对于线性的情况下, LinearSVC由liblinear实现比LIBSVM为基础的SVC更有效率,并且几乎可以线性扩展到数百万的样品和/或功能。
2.5 Tips on Practical Use
- 避免数据复制:对SVC,SVR,NuSVC和NuSVR,如果通过传输数据不是C-ordered contiguous的,而双精度,它在调用底层的C实现之前会复制,我们可以通过检查numpy array的flags属性来判断其是否是C-ordered contiguous。
对于LinearSVC(和LogisticRegression)通过作为numpy的阵列的任何输入将被复制并转化为liblinear内部稀疏数据表示(双精度浮点数和非零分量的INT32索引)。如果你想以适应大规模线性分类不复制密集numpy的C-连续的双精度数组作为输入,我们建议使用SGDClassifier类代替。目标函数可以被配置成大致相同的LinearSVC 模型。 - 内核缓存大小:对SVC,SVR,NuSVC和NuSVR,内核缓存的大小对运行时间有很大的影响。如果你有足够的可用RAM,建议设置cache_size为比200(MB)的默认更高的值,如500(MB)或1000(MB)。
- 设置参数C:在默认情况下C是1,这是一个合理的默认选择。如果你有很多嘈杂的观测,你应该减少它。它对应于更正规化的估计。
LinearSVC和LinearSVR对C不敏感,当它变大,并且预测结果在一定的阈值后停止提高。同时,较大的C值将需要更多的时间来训练,有时高达10倍长。 - 支持向量机算法不是比例无关的,所以它强烈建议缩放您的数据。例如,缩放输入矢量X的每个属性到[0,1]或[-1,+1]的,或标准化它具有均值为0,方差为1。请注意,相同的缩放必须施加到测试向量以得到有意义的结果。见预处理数据上缩放和规范化的更多细节。
- 参数nu在NuSVC/ OneClassSVM/ NuSVR 近似于训练误差和支持向量的分数。
- 在SVC,如果分类数据不平衡(如许多正面极少负面),设置class_weight='balanced’和或尝试不同的惩罚参数C。
- 底层实现随机性:SVC和NuSVC的底层实现使用一个随机数发生器清洗数据用于概率估计(当probability被设置为 True)。这种随机性可以通过控制random_state参数。如果probability设置为False
这些估计不是随机的,并且random_state对结果没有任何影响。OneClassSVM底层实现类似于的SVC和NuSVC。由于OneClassSVM没有概率估计,所以不是随机的。
LinearSVC底层实现使用一个随机数发生器去选择特征时,并且使用双坐标下降拟合模型(当dual被设置为True)。因此,对于相同的输入数据有略微不同的结果并不少见。如果出现这种情况,请尝试使用一个较小的TOL参数。这种随机性也可通过控制random_state参数实现。当dual设置为False底层实现的LinearSVC是并不是随机的,random_state对结果没有任何影响。 - 使用LinearSVC(loss=‘l2’, penalty=‘l1’, dual=False)提供L1惩罚会产生稀疏解,也就是仅不同于零特征权重的子集对决定函数产生影响。增加C会生成更复杂的模型(多个特征被选择)。产生一个“空”模型(所有重量等于零)值可以使用l1_min_c计算。
2.6 kernel function
该内核函数可以是任何如下:
linear: ⟨ x , x ′ ⟩ \left\langle x, x^{\prime}\right\rangle ⟨x,x′⟩
polynomial: ( γ ⟨ x , x ′ ⟩ + r ) d \left(\gamma\left\langle x, x^{\prime}\right\rangle+ r\right)^{d} (γ⟨x,x′⟩+r)d, d 代表关键词 degree, r代表coef0.
rbf: exp ( − γ ∥ x − x ′ ∥ 2 ) \exp \left(-\gamma\left\|x-x^{\prime}\right\|^{2}\right) exp(−γ∥x−x′∥2) γ \gamma γ由关键字指定gamma,必须大于0。
sigmoid: ( tanh ( γ ⟨ x , x ′ ⟩ + r ) ) \left(\tanh \left(\gamma\left\langle x, x^{\prime}\right\rangle+ r\right)\right) (tanh(γ⟨x,x′⟩+r)) 其中r被指定coef0
不同的内核是通过关键字内核在初始化规定:
>>> linear_svc = svm.SVC(kernel='linear')
>>> linear_svc.kernel
'linear'
>>> rbf_svc = svm.SVC(kernel='rbf')
>>> rbf_svc.kernel
'rbf'
2.6.1 custom kernel
您可以通过给内核作为一个Python函数或通过预先计算的Gram矩阵定义自己的内核。
与自定义内核分类的行为方式与任何其他分类相同,不同之处在于:
- 现场support_vectors_现在是空的,只有支持矢量的索引存储在support_
- fit() 方法第一个参数引用(而不是复制)被存储以供将来参考。如果在fit()和predict()阵列变化你会有意想不到的效果。
2.6.1.1 Using Python functions as kernels
你可以在构造函数中把函数传递给关键字kernel来自定义你的kernel函数
你的内核必须以两个矩阵(n_samples_1, n_features)(n_samples_2, n_features) 作为参数输入, 并返回核矩阵(n_samples_1, n_samples_2)
下面的代码定义线性核,并创建一个将使用的内核的分类器的实例:
>>> import numpy as np
>>> from sklearn import svm
>>> def my_kernel(X, Y):
... return np.dot(X, Y.T)
...
>>> clf = svm.SVC(kernel=my_kernel)
2.6.1.2 Using the Gram matrix
设置kernel=‘precomputed’,拟合方法中传入Gram矩阵,而不是X。这里,训练向量和测试向量之间的核值必须提供。
>>> import numpy as np
>>> from sklearn import svm
>>> X = np.array([[0, 0], [1, 1]])
>>> y = [0, 1]
>>> clf = svm.SVC(kernel='precomputed')
>>> # linear kernel computation
>>> gram = np.dot(X, X.T)
>>> clf.fit(gram, y)
SVC(C=1.0, cache_size=200, class_weight=None, coef0=0.0,
decision_function_shape='ovr', degree=3, gamma='auto_deprecated',
kernel='precomputed', max_iter=-1, probability=False,
random_state=None, shrinking=True, tol=0.001, verbose=False)
>>> # predict on training examples
>>> clf.predict(gram)
array([0, 1])
2.6.1.3 Parameters of the RBF Kernel
使用径向基函数(RBF)内核训练的SVM,两个参数必须考虑:C和gamma。参数C,通用于所有SVM内核,分类精度和决策面光滑的权重系数。低C作决策表面光滑,而高C的目标,在所有的训练例子正确分类。 gamma定义了一个训练例子多大的影响力了。越大gamma,越靠近其它实例必须受到影响。
正确选择C和gamma是对SVM的性能至关重要。其中一个建议使用sklearn.model_selection.GridSearchCV时, C和gamma成倍相隔很远以选择良好的参数。
3. Udacity mini-project
4. 参考文献
- SVM支持向量机原理及核函数
- https://scikit-learn.org/stable/modules/svm.html

