计量技术与应用知识点总结

第1章 计量学概论

1. 计量工作的主要任务: 保障单位制的统一和量值的准确可靠.
2. 计量的主要途径和手段: 量值传递及其逆过程量值溯源.
3. 计量的具体内容包括:
   • 研究计量单位及其基准,标准的建立,复制,保存和使用
   • 研究计量方法和计量器具的计量特性
   • 研究计量的不确定度
   • 研究计量人员的计量能力以及计量法制和管理
4. 计量的分类
   • 科学计量
   • 工程计量
   • 法制计量

第2章 量和单位

§2.1.量与量纲

1. 量的分类:
   • 量按其性质,可以分为可测量和可数量.
   • 按照彼此间的关系,可以分为基本量和导出量
2. 量制: 彼此间存在确定关系的一组量.
3. 量纲: 以给定量制中的基本量的幂的乘积表示某量的表达式.

§2.2.计量单位

1. 单位: 计量单位是根据约定定义和采用的标量,任何其它同类量可与其比较,使两个量之比用一个数表示.
2. 单位制
   • 单位制的定义: 单位制是对于给定量制的一组基本单位,导出单位,其倍数单位和分数单位及使用这些单位的规则.
   • 国际单位制的7个基本单位: 米,千克,秒,安培,开尔文,摩尔和坎德拉
3. 基本物理常数: 基本物理常数是指自然界中一些普遍适用的常数,他们不随时间,地点或环境条件的影响而变化,是表征物理现象的定值.

第3章 量值传递与计量检定

§3.1.量值传递

量值传递系统

1. 量值传递系统的构成:

   • 从能复现单位量值的国家基准开始,通过各级计量标准器具逐级传递.最后传递给工作计量器具.
   • 国家基准由国务院计量行政部门负责建立.各级法定计量机构的计量标准受同级政府计量部门的区域管理.
   • 各级计量行政部门最终受国务院计量行政管理部门领导.

2. 计量法规体系的组成

   • 计量行政法规
   • 计量技术法规: 包括国家计量检定系统表,计量器具检定规程,国家计量技术规范

3. 量值传递的方式:

   • 用实物标准进行逐级传递
   • 用计量保证方案进行逐级传递(MAP)
   • 用发放标准物质进行量值传递(CRM):重点掌握
   • 用发播信号进行量值传递

   其中使用CRM进行量值传递的流程图如下:

   基本单位

   公认的定义测量法

   一级CRM

   标准方法

   二级CRM

   现场方法

   用户

   研究和评价标准方法,
   控制二级CRM的研制和生产,
   高精度计量器具的校准

   研究和评价现场方法,
   一般计量器具的校准

计量基准与计量标准

1. 计量器具的分类: 计量器具按其计量学用途或在统一单位值中的作用,可分为计量基准器具,计量标准器具和工作用计量器具
2. 计量标准: 计量标准是将计量基准量值传递到工作计量器具的一类计量器具.
3. 计量基准: 计量基准是在特定领域内具有最高计量特性的计量标准.包括国家标准,副基准,工作基准.
4. 计量基准的发展趋势:初级人工基准→宏观自然标准→高级人工标准→微观自然标准.

§3.2.计量检定

1. 计量检定:
   • 计量检定的定义: 是指查明和确认计量器具是否符合法定要求的程序,它包括检查,加标记和(或)出具检定证书.
   • 计量检定的意义: 检定是进行量值传递或量值溯源以及保证量制准确一致的重要措施.
2. 检定方法的分类: 整体检定和单元检定.
3. 计量检定系统表:
   • 计量检定系统表的定义: 国家计量检定系统表用图表结合文字的形式,规定了国家计量基准所包括的全套主要计量器具和主要计量特性,从计量基准通过计量标准向工作计量器具进行量值传递的程序,指明误差以及基本检定方法等.它反映了测量某个量的计量器具等级的全貌,因而又称为计量器具等级图.
   • 计量检定系统表的内容
     • 引言
     • 计量基准器具
     • 计量标准器具
     • 工作计量器具
     • 检定系统框图
4. 计量检定规程
   • 计量检定规程的定义: 计量检定规程是指为评定计量器具的计量特性,规定了计量性能,法制计量控制要求,检定条件和检定方法以及检定周期等内容,并对计量器具做出合格与否的判定的计量技术法规.
   • 计量检定规程的内容:
     • 引言
     • 概述
     • 技术要求
     • 检定条件
     • 检定项目
     • 检定方法
     • 检定结果的处理
     • 检定周期
     • 附录

第5章 计量管理与监督

1. 计量管理工作主要包括: 科学计量,法制计量和工程计量3部分.
2. 计量管理的内容: 从狭义上说,计量管理是对计量单位制,计量器具等的管理,主要包括计量单位的管理,量值传递的管理,计量器具的管理和计量机构的管理四个方面.

第6章 温度计量

§6.1.温度与温度计量

1. 温度的定义: 温度是表征物体冷热程度在热平衡中的状态的物理量.
2. 温度计量的定义: 温度计量是研究制定和实施温度标准,测温方法,测温装置以及如何将热变为温度量值或作为控制信号,保证温度量值统一准确可靠的一系列工作.

§6.2.ITS-90国际温标

1. ITS-90的由来: ITS-90温标是在1968年国际实用温标的基础上经过重大修改制定的.其通过年份为1989年.

2. ITS-90温标与摄氏温标,华氏温标的区别: 摄氏温标,华氏温标为经验温标,而ITS-90为热力学温标,两者互相区别.

3. 温度的单位:热力学温度的单位为开尔文($K$),定义水三相点热力学温度的1/273.16为1$K$

4. 热力学温度($T_{90}$)与摄氏温度($t_{90}$)的转换关系为
   $$t_{90}=T_{90}-273.15$$

   根据以上定义,水的冰点为0℃,水的三相点为0.01℃.

5. ITS-90国际温标的定义:ITS-90根据不同温区来进行定义

   • 0.95K~5.0K温区

   • 3.0K~24.5561K温区

   • 13.8033K~961.781K温区: 在该温区存在参考函数和偏差函数的概念

     • 电阻比: 温度值$T_{90}$是由该温度时的电阻$R(T_{90})$与水三相点时的电阻$R(273.16K)$之比来求得的.在计算时使用电阻比的概念,其定义为
       $$W(T_{90})=\frac{R(T_{90})}{R(273.16K)}$$

     • 其中,$T_{90}$的值可以由参考函数的$W_r(T_{90})$值,以及偏差函数$\Delta W(T_{90})$的值经过运算后得到

     • 由$W(T_{90})$值计算$T_{90}$的计算过程为: 由$W(T_{90})$→$\Delta W(T_{90})$→$W_r(T_{90})$→$T_{90}$.

       • $W_r(T_{90})$的值可以由参考函数[$W_r=f(T_{90})$]得到,参考函数的自变量是温度.
       • $\Delta W(T_{90})$的值可以由偏差函数[$\Delta W=W-W_r$]得到,偏差函数的自变量是电阻比的测量值.

   • 961.78K以上温区

§6.3.标准温度计

膨胀式温度计

1. 玻璃液体温度计

   • 误差来源: 读数误差, 标尺位移, 零点误差, 露出液柱的影响, 非线性误差, 滞后误差, 液柱断裂

2. 压力式温度计

   • 测温原理: 基于物质受热膨胀的原理,但它不是靠物质受热膨胀后体积变化来指示温度,而是靠在密闭容器中压力变化来指示温度.
     $$p_t-p_0=\frac{\alpha }{\beta }(t-t_0)$$

3. 双金属温度计

   • 测温原理: 双金属片是将两片线膨胀系数不同的金属片叠焊在一起制成的.双金属片受热后,由于膨胀系数大的主动层B的膨胀量大于膨胀系数小的被动层A,造成了双金属片向被动层A一侧弯曲.在规定的温度范围内,双金属片的偏转角与温度有关.

热电偶温度计

1. 热电偶温度计的结构

   • 热电偶是由两根不同的导体(或半导体)A和B焊接或铰接而成.
   • 热端(工作端,测量端): 焊接的一端,测温时放在被测对象中
   • 冷端(自由端,参比端): 导线连接的一端

2. 热电偶测温的基本原理

   热电偶的热电势由接触电势和温差电势两部分组成

   • 接触电势$e_{AB}(t)$: 由于接触的两种导体的电子密度不同而产生的电势,其数值取决于两种材料的性质和接触点的温度.

   • 温差电势$e_A(t,t_0)=e_A(t)-e_A(t_0)$: 由于导体两端温度差而产生的电势,其数值取决于材料的性质和其两端的温度.

   • 热电偶回路总电势: 整个回路的热电势$E_{AB}$是由两个接触电势$e_{AB}(t)$和$e_{AB}(t_0)$和两个温差电势$e_A(t,t_0)$和$e_B(t,t_0)$组成.

     
     $$\begin{array}{rl}{E}_{AB}(t,t_0)& =e_{AB}(t)-e_{AB}(t_0)-[e_A(t,t_0)-e_B(t,t_0)]\\ & =[e_{AB}(t)-e_{AB}(t_0)]-[e_A(t)-e_A(t_0)-e_B(t)+e_B(t_0)]\\ & =[e_{AB}(t)+e_B(t)-e_A(t)]-[e_{AB}(t_0)+e_B(t_0)-e_A(t_0)]\\ & =f_{AB}(t)-f_{AB}(t_0)\end{array}$$

3. 热电偶的基本定律: 均质导体定律,中间导体定律,中间温度定律

4. 标准化热电偶: 标准化热电偶是指在工业上大量生产和使用,工艺稳定,性能符合专业标准或国家标准,同时具有统一分度表的热电偶.

5. 热电偶的冷端温度补偿方法: 冷端恒温法, 计算修正法, 补偿导线法, 机械零点调整法, 补偿电桥法(冷端温度补偿器).

热电阻温度计

1. 热电阻的测温原理: 热电阻温度计就是利用导体(半导体)的温度随着阻值变化这一特性来进行温度测量的,温度变化引起的导体(或半导体)的电阻变化,通过测量桥路转换成电压(毫伏级)信号,然后送入显示仪表以指示和记录被测温度.

2. 电阻温度系数$\alpha$:表征电阻与温度之间灵敏度的参数,其定义为温度每变化1℃时,材料电阻的相对变化率,即
   $$\alpha =\frac{1}{R}\frac{dR}{dt}\approx \frac{R_{100}-R_0}{R_0\times 100}$$

3. 热电偶的分度号:

   • 铜热电阻的分度号有$C{u}_{50}$和$C{u}_{100}$,表示其在0℃时的阻值分别为50Ω和100Ω
   • 铂热电阻的分度号有$P{t}_{10}$和$P{t}_{100}$,表示其在0℃时的阻值分别为10Ω和100Ω

4. 热电阻的引出线存在两线制,三线制和四线制三种,但是热电偶没有这种说法.

§6.4.热电偶温度计的检定

标准热电偶的检定

1. 标准热电偶的分度:

   • 标准热电偶的$E\sim t$分度关系为多项式关系,即
     $$E(t)=\sum _{i=1}^n{a}_i{t}^i$$

   • 偏差$\Delta E$与温度$t$呈简单的多项式函数关系,即
     $$\Delta E=a+bt+c{t}^2$$

   由上面两式可以求得该只热电偶的分度关系为
   $$E(t)=E_r(t)+\Delta E$$

   式中:

   • $E_r(t)$表示选定的一支典型热电偶的热电势函数,称为参考函数
   • $E(t)$表示待确定的热电偶的热电势函数

2. 标准热电偶的分度误差:标准热电偶的分度误差是标准热电偶在各标准等级浮现温度的极限误差,由不确定度$\delta$来表示.
   $$\delta =\sqrt{\sum _{i=1}^n{\delta }_i^2}$$

热电偶的检定方法

热电偶的检定方法有三种:

• 双极法: 不要求被检定的热电偶和标准热电偶的型号相同.
• 同名极法: 要求被检定的热电偶和标准热电偶的型号相同.
• 微差法: 要求被检定的热电偶和标准热电偶的型号相同.

热电偶的检定会出计算题

1. 在300℃以下,热电动势误差$\Delta e_t$用下式计算:
   $$\Delta e_t={\bar{e}}_{被}+S_{被}\cdot \Delta t_{检}-e_{分}$$

   式中:

   • ${\bar{e}}_{被}$表示被检热电偶在检定点附近温度下,测得的热电动势算术平均值

   • $S_{被}$表示被检热电偶在检定点温度的微分热电动势

   • $e_{分}$表示被检热电偶分度表上查得的某检定点温度的热电动势值
     $$\Delta t_{检}=t_{检}-t_{实}$$

   • $t_{检}$表示检定点温度

   • $t_{实}$表示实际温度(实际温度=读数平均值+修正值)

   • $\Delta t_{检}$表示检定点温度与实际温度的差值

   题目: 在200℃检定点附近,参考端为0℃,被检E型热电偶的热电动势值为13.452mV,2等标准水银温度计测得现场的温度为200.15℃,求被测热电偶在200℃时示值误差.

   解答:
   $$\Delta t_{检}=200-200.15=-0.15^{\circ }C$$

   从检定分度表查得,在200℃时热电偶的热电动势和微分热电动势
   $$\begin{gathered} e_{分}=13.421mV \\ {S}_{被}=0.074mV \end{gathered}$$

   则可计算出$\Delta e_{200}$,即:
   $$\begin{array}{rl}\Delta e_{200}& =\bar{e}+S_{被}\cdot \Delta t-e_{分}\\ & =13.452+0.074\times (-0.15)-13.421\\ & =0.020mV\end{array}$$

   则热电偶在200℃时示值误差:
   $$\Delta t_{200}=\frac{\Delta e_{200}}{S_{被}}=\frac{0.020}{0.074}=0.3^{\circ }C$$

2. 在300℃以上,热电动势误差$\Delta e_t$用下式计算:

   $$\Delta e_t={\bar{e}}_{被}+\frac{e_{标}-{\bar{e}}_{标}}{S_{标}}\cdot S_{被}-e_{分}$$

   式中:

   • ${\bar{e}}_{被}$表示被检热电偶在检定点附近温度下,测得的热电动势算术平均值
   • $e_{标}$表示标准热电偶证书上检定点温度的热电动势值
   • ${\bar{e}}_{标}$表示标准热电偶在检定点附近温度下,测得的热电动势算术平均值
   • $e_{分}$表示被检热电偶分度表上查得的某检定点温度的热电动势值
   • $S_{标}$,$S_{被}$表示标准,被检热电偶在某检定点温度的微分热电动势

   题目:在1000℃附近测得标准铂铑10-铂热电偶的热电动势算术平均${\bar{e}}_{标}$值为9. 558mV;被检N型热电偶的热电动势算术平均值${\bar{e}}_{被}$为36.274mV.从标准热电偶检定证书中查得1000℃时热电动势$e_{标}$为9.581mV;求被检N型热电偶在1000℃时的误差.从热电偶微分热电动势表中查得1000℃时,标准与被检热电偶1℃分别相当于0.012mV,0.039mV.

   解答: 从N型热电偶分度表中查得1000℃时热电动势为36.256mV.将以上数据代入下式,可计算出误差$\Delta e$值.即:
   $$\begin{array}{rl}\Delta e& ={\bar{e}}_{被}+\frac{e_{标}-{\bar{e}}_{标}}{S_{标}}\cdot S_{被}-e_{分}\\ & =36.274+\frac{9.581-9.558}{0.012}\times 0.039-36.256\\ & =0.093mV\end{array}$$

   则热电偶在1000℃时示值误差:
   $$\Delta t_{200}=\frac{\Delta e}{S_{被}}=\frac{0.093}{0.039}=2.4^{\circ }C$$

   其修正值为-2.4C

§6.5.热电阻温度计的检定

标准铂热电阻温度计的分度计算方法

标准铂热电阻温度计的检定有两种方法: 定点法和比较法

定点法

定点法的检定点温度为$T_{90i}$,定点法计算分为两种情况:

1. 由$W(T_{90})$计算$T_{90}$,步骤如下:

   1. 计算$W(T_{90i})=\frac{R(T_{90i})}{R(273.16K)}=\frac{R(T_{90i})}{R_{tp}}$
   2. 利用参考函数计算$W_r(T_{90i})$
   3. 由偏差方程组$\Delta W(T_{90i})=f[W(T_{90i})]$,确定偏差函数中的系数a,b,c的值
   4. 由$W(T_{90})=W_r(T_{90})+\Delta W(T_{90})$,得$W_r(T_{90})=W(T_{90})-\Delta W(T_{90})$,使用$W_r(T_{90})\sim T_{90}$的反函数直接计算$T_{90}$

2. 由$T_{90}$计算$W(T_{90})$,步骤如下:

   1. 建立迭代方程: $W_n(T_{90})=W_r(T_{90})+f[W_{n-1}(T_{90})]$,其中$f[W_{n-1}(T_{90})]$为偏差函数.

   2. 迭代计算过程:

      令初始值$W_0(T_{90})=W_r(T_{90})$,则有
      $$\begin{gathered} W_1(T_{90})=W_r(T_{90})+f[W_0(T_{90})] \\ {W}_2(T_{90})=W_r(T_{90})+f[W_1(T_{90})] \\ ... \end{gathered}$$

      第$n$次计算后,当$|W_n(T_{90})-W_{n-1}(T_{90})|<Z=10^{-8}$时,则
      $$W(T_{90})=W_n(T_{90})$$

例题: 某标准铂热电阻温度计,试确定其在83.8058~273.16K温区内的分度计算式.

解答: 测量水的三相点,氩的三相点,汞的三相点的电阻值,由电阻比的定义计算得到
$$W(83.8058K)=0.21612827,W(234.3156K)=0.84419846$$

查表计算在83.8058K,273.16K温度的参考函数值
$$W_r(83.8058K)=0.21585974,W_r(234.3156K)=0.84414220$$

计算偏差值
$$\Delta W(83.8058K)=0.00026853,\Delta W(234.3156K)=0.00001358$$

由83.8058~273.16K温区内的偏差函数(ITS-90温标给出)
$$\Delta W(T_{90})=a[W(T_{90})-1]+b[W(T_{90})-1]\ln W(T_{90})$$

得到
$$\{\begin{array}{rl}0.00026853& =a(0.21612827-1)+b(0.21612827-1)\ln 0.21612827\\ 0.00005626& =a(0.84419846-1)+b(0.84419846-1)\ln 0.84419846\end{array}$$

解上述方程组,得到
$$\{\begin{array}{r}a=-0.00036340\\ b=-0.00001358\end{array}$$

故求得该标准铂电阻的偏差函数$\Delta W(T_{90})=-0.00036340[W(T_{90})-1]-0.00001358[W(T_{90})-1]\ln W(T_{90})$

因此,该支标准铂热电阻温度计的分度计算公式为
$$W(T)=W_r(T)-0.00036340[W(T_{90})-1]-0.00001358[W(T_{90})-1]\ln W(T_{90})$$

比较法

检定点温度$T_i$是由恒温装置提供,但未必是规定要求的检定点温度$T_{90i}$,此时的计算方法如下:

1. 根据标准器标准铂电阻的阻值,计算$W_{标}(T_i)=\frac{R_{标}(T_i)}{R_{标}(273.16k)}$,根据被检铂电阻的阻值,计算$W(T_i)=\frac{R(T_i)}{R(273.16k)}$
2. 根据$W_{标}(T_i)$计算$T_i$,这可由标准铂电阻温度计的分度计算公式直接得到
3. 计算$T_i$(测试点)的参考函数$W_r(T_i)$
4. 计算被检铂电阻的偏差函数值(在$T_i$点): $\Delta W(T_i)=W(T_i)-W_r(T_i)$
5. 由偏差函数方程组没确定偏差函数中系数$a$,$b$,$c_i$的值.
6. 此时,得到被检铂电阻的分度计算公式: $W(T)=W_r(T)+\Delta W(T)$
7. 计算规程要求的检定点温度$T_{90i}$的$W(T_{90i})$值: 由$T_{90i}$计算出$W(T_{90i})$,采用迭代近似计算,方法同定点法的要求,特别是评价合格要求的$W(T_{90i})$值要算出.

工业铂热电阻温度计的检定

1. 被检工业热电阻$R(0^{\circ }C)$的计算
   $$R(0^{\circ }C)=R(t_i)-{\frac{dR}{dt}|}_{t=0^{\circ }C}\cdot t_i$$

   式中:

   • $R(t_i)$表示被检定工业热电阻在冰点槽温度$t_i$时的电阻值(测量值)

   • ${\frac{dR}{dt}|}_{t=0^{\circ }C}$表示被检定工业热电阻在$0^{\circ }C$时的电阻变化率,是可计算的已知值

     对于工业铂电阻温度计${\frac{dR}{dt}|}_{t=0^{\circ }C}=0.00391R^{\ast }(0^{\circ }C)$
     对于工业铜电阻温度计${\frac{dR}{dt}|}_{t=0^{\circ }C}=0.00428R^{\ast }(0^{\circ }C)$

   • $R^{\ast }(0^{\circ }C)$表示被检定工业热电阻在0℃时的名义值.

2. 被检工业热电阻在0℃时的温度偏差$E(0^{\circ }C)$的计算:
   $$E(0^{\circ }C)=\frac{R(0^{\circ }C)-R^{\ast }(0^{\circ }C)}{{\frac{dR}{dt}|}_{t=0^{\circ }C}}$$

3. 被检工业热电阻$\alpha$的计算:

   热电阻温度系数$\alpha$表示0~100℃范围内单位温度电阻的变化率
   $$\alpha =\frac{R(100^{\circ }C)-R(0^{\circ }C)}{100R(0^{\circ }C)}$$

   因此,我们需要计算被检定热电阻$R(100^{\circ }C)$的值,计算步骤如下:

   1. 计算恒温油槽温度$t_b(\approx 100^{\circ }C)$与100℃的偏差:
      $$\Delta t=t_b-100=\frac{R_{标}(t_b)-R_{标}(100^{\circ }C)}{{\frac{dR}{dt}|}_{标t=100^{\circ }C}}$$

      式中:

      • $R_{标}(100^{\circ }C)$表示标准铂电阻温度计在100℃的电阻值,由标准铂热电阻温度计证书给出的分度公式计算求出

      • ${\frac{dR}{dt}|}_{标t=100^{\circ }C}$表示标准铂电阻温度计在100℃时的电阻变化率

        ${\frac{dR}{dt}|}_{标t=100^{\circ }C}=0.00387R_{标tp}$

   2. 计算被检定工业热电阻100℃时的阻值:
      $$R(100^{\circ }C)=R(t_b)-{\frac{dR}{dt}|}_{t=100^{\circ }C}\cdot \Delta t$$

      式中:

      • ${\frac{dR}{dt}|}_{t=100^{\circ }C}$表示被检定工业热电阻在0℃时的电阻变化率,是可计算的已知值

        对于工业铂电阻温度计${\frac{dR}{dt}|}_{t=0^{\circ }C}=0.00379R^{\ast }(0^{\circ }C)$
        对于工业铜电阻温度计${\frac{dR}{dt}|}_{t=0^{\circ }C}=0.00428R^{\ast }(0^{\circ }C)$
        0

第7章 压力计量

§7.1.压力计量的概述

1. 压力的分类:
   • 大气压力: 大气自重所产生的压力.
   • 绝对压力: 以零为参考压力的压力.
   • 表压力: 以大气压力为参考压力的压力,在不混淆的情况下简称为压力.
   • 真空度: 低于大气压力的绝对压力.
2. 压力计量中的常用参数
   • 重力加速度
   • 密度: 分为气体的密度和液体的密度
3. 压力量值的传递

   • 压力量值传递的定义: 压力量值的传递是指通过检定将压力的国家基准所复现的压力单位量值通过标准逐级传递,一直传递到工作用压力计量器具,以保证由被测对象所得到的压力量值的准确性和一致性.

   • 压力计量器具检定系统图

     

§7.2.压力标准器

液体压力计

1. 标准U型管液体压力计

   • 工作原理: 液体压力计是利用压力计中的液柱产生的静压力去平衡被测压力的原理进行测压的.U型管内注入工作介质(封液)到零位处,肘管的一段被接至被测压力$P$,另一端连通大气,其压力为大气压力$P_D$.U型管内的封液在被测压力$P$和大气压力$P_D$的共同作用下,在肘管内将产生液柱的高度差.当被测压力$P$一定时,在U型管中产生的液柱高度差也是一定的.

     

     根据流体静力学原理可以得到静力平衡方程式.
     $$p=(\rho -{\rho }_1)g(h_1+h_2)+({\rho }_2-{\rho }_1)g(H+h_2)$$

     对于一,二,三等标准压力计,计算压力值时使用下式:
     $$p=(\rho -{\rho }_1)g(h_1+h_2)$$

     对于工作用压力计,计算压力值时使用下式:
     $$p=\rho g(h_1+h_2)$$

   • 误差来源:

     • 压力计的使用温度
     • 重力加速度
     • 毛细现象
     • 读数误差
     • U型管安装的位置
     • 压缩空气柱的高度
     • 标尺的刻度精度

2. 补偿式微压计: 知道名称就行

   

弹簧管式压力计

1. 弹簧管压力表:

   • 弹簧管压力表的输出表达式:
     $$\Delta \gamma =\frac{\Delta b}{b+\Delta b}\gamma$$

   • 增加弹簧管压力表灵敏度的方法: 从上面输出表达式可以推出两个方法

     • 缩短管截面短轴$b$
     • 采用多圈弹簧管

活塞式压力计

1. 活塞式压力计
   • 工作原理: 活塞式压力计是利用作用在活塞上的砝码重力与被测压力作用在活塞上所产生的力相平衡的原理工作的.当作用在活塞上的两个力平衡时,所加载法码的重力就代表了被测压力值.
   • 性能参数:
     • 测压范围
     • 密封性
     • 活塞的有效面积
     • 活塞下降速度: 取决于活塞间隙的漏流大小.
     • 活塞转动延续时间: 在规定的起始转速下,活塞自由转动的时间
     • 灵敏限
     • 允许误差
     • 活塞系统受压变形

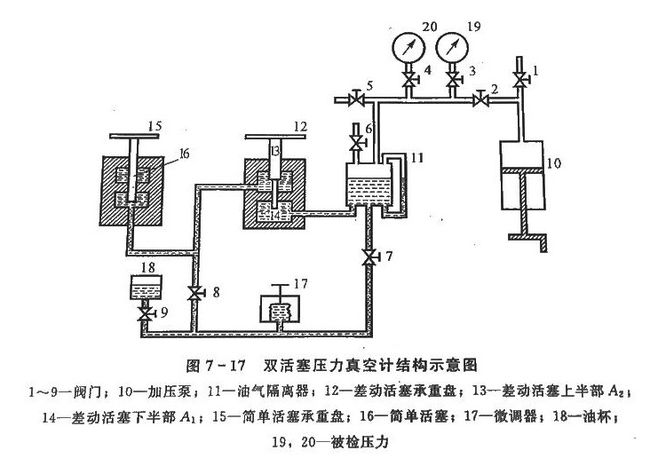
双活塞压力真空计

1. 双活塞压力真空计对活塞式压力计做的改进:

   • 活塞做成空心状,以减轻活塞自重和降低压力计的测量下限
   • 改活塞与活塞筒的全面接触为两个环的接触,由此减小接触摩擦,提高灵敏限
   • 为了增大转动惯量而将砝码制成空心状,增加了砝码半径,由此提高活塞转动延续时间
   • 使用气体做传压介质,减小由液柱引起的误差
   • 附加一个固定的压力,使活塞存在一个起始平衡零点,从而把测量下限降至0

2. 工作原理: 重点掌握三个平衡调整过程

   • 零位平衡调整:

     1. 打开阀门6,7,8,9,油气隔离器通大气,大气压通过工作介质(变压器油)作用于简单活塞和差动活塞
     2. 启动电机,使两个活塞转动(减小活塞的摩擦阻力)
     3. 调整微调器门,改变油气隔离器内工作介质的液面高度,使两活塞稳定地处于工作位置,达到力平衡状态.平衡的调整也可以通过向承重盘加(减)小砝码的方法来实现.

     平衡状态时,有方程式:
     $$\frac{m_{2}g}{A_3}(A_2-A_1)+\rho gh{A}_1=m_{1}g\text{\hspace{1em}(7.1)}$$

     式中:

     • $m_1$表示差动活塞及其连接件的质量,kg
     • $m_2$表示简单活塞及其连接件的质量,kg
     • $A_1$表示差动活塞下部小活塞有效面积
     • $A_2$表示差动活塞上部大活塞有效面积
     • $A_3$表示简单活塞有效面积
     • $\rho$表示工作介质(变压器油)的密度
     • $b$表示油气隔离器页面与差动活塞下端面之间的液柱高度

   • 测压平衡调整

     1. 关闭阀门1,5,6,7,8,9,使压力计的压力系统与大气压力隔离,成为密闭状态
     2. 打开阀门2,3,4,使压力计的压力系统与加压泵,被检定压力压力计接通
     3. 用加压泵加压(手轮摇进),差动活塞的承重盘12上升,简单活塞承重盘15下降
     4. 在承重盘12上加砝码,调整加压情况下的平衡,直至使两活塞恢复到平衡位置,调整过程中,承重盘12下降,承重盘15上升.

     测压平衡状态时,有方程:
     $$\frac{m_{2}g}{A_3}(A_2-A_1)+\rho gh{A}_1+p{A}_1=(m_1+m_1^{\prime })g\text{\hspace{1em}(7.2)}$$

     式中:

     • $m_1^{\prime }$表示承重盘12上所加砝码的质量
     • $p$表示被测压力(加压泵所加压力)

     由方程式(7.1)和(7.2)得到
     $$p=\frac{m_1^{\prime }g}{A_1}$$

   • 真空测量的调整

     1. 关闭阀门1,5,6,7,8,9,使压力计的压力系统与大气压力隔离,成为密闭状态.
     2. 加压泵首轮退出产生负压,承重盘12下降,承重盘15上升.
     3. 在承重盘15上加砝码,调整真空情况下的平衡,直至两活塞恢复到平衡位置.调整过程中承重盘12上升,承重盘15下降.

     真空平衡状态时,有方程:
     $$\frac{(m_2+m_2^{\prime })g}{A_3}(A_2-A_1)+\rho gh{A}_1+p{A}_1=m_{1}g\text{\hspace{1em}(7.3)}$$

     式中:

     • $m_2^{\prime }$表示承重盘15上所加砝码的质量

     由方程式(7.1)和(7.3)得到
     $$\begin{gathered} p=-\frac{m_2^{\prime }g}{A_1{A}_3}(A_2-A_1)=-K\frac{m_2^{\prime }g}{A_1} \\ K=\frac{A_2-A_1}{A_3} \end{gathered}$$

§7.3.常用压力计的检定

1. 液体压力计的检定项目:
   • 外观检定
   • 密封性检查
   • 零位误差的检定
   • 示值检定
   • 示值的修正
2. 弹簧管压力计的检定项目:
   • 环境条件
   • 外观检查
   • 示值检定
3. 活塞式压力计的检定项目:
   • 外观检查
   • 校验器的密封性检定
   • 承重盘平面对活塞中心线的垂直度检定
   • 活塞转动延续时间的检定
   • 活塞下降速度检定
   • 活塞有效面积检定
   • 鉴别力的检定

第8章 流量计量

§8.1.流量计量概述

1. 流量的概念及分类:

   • 流量: 流量是指流体流过一定截面的体积或质量与时间之比.
   • 流量的分类
     • 瞬时流量: 单位时间内流过某一截面流体的数量.
     • 累计流量: 一段时间内流过某一截面流体的数量.

2. 流体的流动状态:

   • 流体可以分为单相流和多相流:
     • 单相流: 管道内只有一种均匀状态流体流动
     • 多相流: 管道内同时用两种及以上的不同流体流动
   • 流体的流动状态分为层流和紊流:
     • 层流: 流体沿管道轴向做分层流动,没有垂直于主流方向的横向运动,流层间互不混杂,有规则的流线
     • 紊流: 随着管内流体速度的增大,流体的流动不仅有轴向的运动,而且还伴随着剧烈的无规则横向运动.

3. 两个流动基本方程:

   • 流动连续性方程(质量守恒)
     $${\rho }_1{u}_1{A}_1={\rho }_2{u}_2{A}_2$$

     式中:

     • $A$表示截面面积
     • $\rho$表示流体密度
     • $u$表示截面上流体平均流速

   • 伯努利方程(能量守恒)
     $$g{z}_1+\frac{p_1}{\rho }+\frac{u_1^2}{2}=g{z}_2+\frac{p_2}{\rho }+\frac{u_2^2}{2}$$

     在实际流动中,考虑到流体与管壁之间的摩擦,公式形式如下:
     $$g{z}_1+\frac{p_1}{\rho }+\frac{u_1^2}{2}=g{z}_2+\frac{p_2}{\rho }+\frac{u_2^2}{2}+h_{wg}$$

     式中:

     • $g$表示重力加速度
     • $z$表示界面相对于某一基准线的高度
     • $p$表示截面上的流体静压力
     • $u$表示截面内流体的平均流速
     • $h_{wg}$表示截面间流体实际流动而产生的机械能损失

4. 流量计量中常用的物理参数:

   • 流体的黏度: 分为动力粘度$\eta$和运动粘度$v$.

     • 流体的动力粘度$\eta$可以用牛顿粘性定律来表示: 流体的动力粘度为流体单位面积上的内摩擦力与流层间的速度梯度之比.
       $$\eta =\frac{F/A}{du/dy}$$

       式中:

       • $F$表示流层间的内摩擦力
       • $A$表示表示流层间的接触面积
       • $du/dy$表示流层间的速度梯度,即流体垂直于速度方向的速度变化率

     • 流体的运动粘度: 流体的动力粘度$\eta$与流体密度$\rho$之比
       $$v=\frac{\eta }{\rho }$$

   • 雷诺数$R_e$

     • 雷诺数的定义: 雷诺数$R_e$表示流体流动雷诺数是指流体流动的惯性力$F_g$与其粘性力(内摩擦力)$F_m$之比.
       $$R_e=\frac{F_g}{F_m}=\frac{v}{\eta }\rho l$$

       当流体在圆管内流动时,雷诺数的流量表达式为
       $$R_{eD}=345\times 10^{-3}\frac{q_m}{D_t\eta }$$

       式中:

       • $v$表示特征流速,在管流中为有效界面上的平均流速,m/s
       • $\rho$表示流体密度,kg/m³
       • $\eta$表示动力粘度
       • $l$表示流束的定型尺寸,在圆管内为管道内径,m
       • $D_t$表示工作温度下的管道内径,mm

     • 雷诺数的意义: 雷诺数是判别流体状态的准则,临界值为2320.雷诺数$R_e$<2320为层流状态,而当雷诺数大于此值时,流动将开始转变为层流状态.

§8.2.静态容积法水流量标准装置

§8.3.静态质量法液体流量标准装置

用比重瓶测量水的密度的步骤如下:

1. 称重空比重瓶
   $$m_1-\frac{m_1}{{\rho }_f}{\rho }_{a}g=M_B-\frac{M_B}{{\rho }_B}{\rho }_{a}g\text{\hspace{1em}(8.3.1)}$$

   式中:

   • $m_1$表示称重空瓶时(在空气中)砝码质量
   • $M_B$表示比重瓶质量(未知)
   • ${\rho }_a$表示空气密度
   • ${\rho }_f$表示砝码材料密度
   • ${\rho }_B$表示比重瓶材料密度

2. 称重装满蒸馏水的比重瓶
   $$m_2-\frac{m_2}{{\rho }_f}{\rho }_{a}g=M_B-\frac{M_B}{{\rho }_B}{\rho }_{a}g+M_{ZW}-\frac{M_{ZW}}{{\rho }_{ZW}}{\rho }_{a}g\text{\hspace{1em}(8.3.2)}$$

   式中:

   • $m_2$表示称重装满蒸馏水比重瓶时砝码质量
   • $M_{ZW}$表示蒸馏水质量(未知)
   • ${\rho }_{ZW}$表示蒸馏水密度(已知)

3. 称重装满工作介质水的比重瓶
   $$m_3-\frac{m_3}{{\rho }_f}{\rho }_{a}g=M_B-\frac{M_B}{{\rho }_B}{\rho }_{a}g+M_{SW}-\frac{M_{SW}}{{\rho }_{SW}}{\rho }_{a}g\text{\hspace{1em}(8.3.3)}$$

   式中:

   • $m_3$表示称重装工作介质水比重瓶时砝码质量
   • $M_{SW}$表示工作介质水质量(未知)
   • ${\rho }_{SW}$表示工作介质水密度(未知,待求量)

联立式(8.3.1)与式(8.3.2)得到比重瓶的容积$V$
$$V=\frac{M_{ZW}}{{\rho }_{ZW}}=\frac{(m_2-m_1)(1-\frac{{\rho }_a}{{\rho }_f})}{({\rho }_{ZW}-{\rho }_a)}\text{\hspace{1em}(8.3.4)}$$

联立式(8.3.1)与式(8.3.3)得到比重瓶的容积$V$
$$V=\frac{M_{SW}}{{\rho }_{SW}}=\frac{(m_3-m_1)(1-\frac{{\rho }_a}{{\rho }_f})}{({\rho }_{SW}-{\rho }_a)}\text{\hspace{1em}(8.3.5)}$$

联立式(8.3.4)与式(8.3.5),有
$$\frac{(m_2-m_1)(1-\frac{{\rho }_a}{{\rho }_f})}{({\rho }_{ZW}-{\rho }_a)}=\frac{(m_3-m_1)(1-\frac{{\rho }_a}{{\rho }_f})}{({\rho }_{SW}-{\rho }_a)}$$

故
$${\rho }_{SW}=\frac{m_3-m_1}{m_2-m_1}({\rho }_{ZW}-{\rho }_a)+{\rho }_a$$

§8.4.标准体积管流量标准装置

§8.5.气体流量标准装置

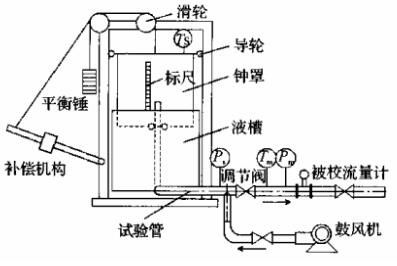
钟罩式气体流量标准装置

1. 测量范围: 钟罩式气体流量标准装置可测量的最大流量可达4500m³/h.

2. 工作原理:

   • 打开连接鼓风机的阀门,关闭调节阀,开启鼓风机(气泵),使气体导入钟罩内,并使得钟罩上升到一定高度.停止鼓风机并关闭与其连接的阀门.
   • 检定流量计时,打开调节阀,调整连接被校流量计的调节阀门.流量稳定后,钟罩以一定的速度下降.钟罩下降到上挡板对准光电发讯器时,发讯器发出开始计时的触发脉冲;钟罩下降到下挡板时,发讯器发出通知及时的触发脉冲.记下钟罩内气体的温度$T_Z$及压力$P_Z$和被检流量计前的气体温度$T$及压力$P$

   下面推导流量计算的公式:

   • 在钟罩工作温度$T_Z$,工作压力$P_Z$状态下,标准流量
     $$q_v(T_Z,P_Z)=\frac{V_Z}{\Delta t}$$

   • 根据气体方程进行气体在两种状态下的换算,有
     $$\frac{P_Z{V}_Z}{Z_Z{T}_Z}=\frac{PV}{ZT}$$

     式中:

     • $V$表示$P_Z$,$T_Z$状态下的气体体积换算为$P$,$T$状态下气体的体积
     • $Z_Z$表示$P_Z$,$T_Z$状态下的气体压缩系数
     • $Z$表示$P$,$T$状态下的气体压缩系数

     故有
     $$V=\frac{Z}{Z_Z}\frac{P_{Z}T}{P{T}_Z}{V}_Z$$

   • 因而换算到在$P$,$T$状态下,标准流量
     $$q_v(P,T)=\frac{V}{\Delta t}=\frac{Z}{Z_Z}\frac{P_{Z}T}{P{T}_Z}\frac{V_Z}{\Delta t}$$

3. 补偿杆的作用: 当钟罩下降时,由于液体槽内的水对钟罩的浮力增大会影响钟罩内压力空间的压力,补偿机构能够使得钟罩内的气体压力保持恒定.它的补偿原理是:装置工作时,钟罩下降,钟罩浸水部分增加,水对钟罩浮力增大,钟罩内压力减小.由于补偿杆与竖直向上的夹角随钟罩的下降而减小,钢丝绳供给钟罩的拉力亦减小,从而补偿了液槽水对钟罩浮力增大对钟罩内气体压力的影响.

4. 钟罩式气体流量标准装置在使用时不必进行钟罩的温度压力影响的修正以及计时误差的修正.

音速喷嘴

壅塞现象: 当喷嘴的下游压力与上游压力之比达到临界状态(对空气是0.528)时,音速喷嘴或喷管的喉部气流会达到音速.即使其下游的压力再下降(意味着下游压力与上游压力之比减小),其流速(流量)也保持稳定.这种现象在流体力学中称为壅塞现象.

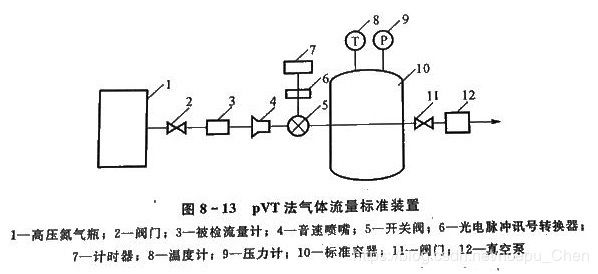
pVT法气体流量标准装置

测试用氮气要求其纯度为99.999%.操作过程是:

1. 用真空泵将标准容器抽真空后,充入氮气,清扫容器.
2. 用真空泵将氮气抽出,直到压力小于1kPa左右.
3. 待容器内的氮气稳定后,测量其压力和温度.
4. 用天平称出高压氮气瓶的质量$m_1$.
5. 将高压氮气瓶(气源)中的氮气充进标准容器内,直到压力达到50kPa左右,记下充气时间.
6. 待容器内氮气稳定后,测量其压力和温度.
7. 用天平称出高压氮气瓶的质量$m_2$

§8.6.标准节流装置的检定

标准节流装置的检定有几何检定法和系数检定法