Neural network and deep learning阅读笔记（4）神经网络学习方式

完整的手写字符识别代码在最下。

Weight initialization

在第一章创建神经网络的时候，曾经对weight和biases进行过初始化，当时是使用了两个独立高斯随机变量（均值为0，标准差为1），这一节看看有没有更好的初始化方法。假设我们现在有一个神经网络有1000个输入神经元，输入层到第一层隐藏层的权重是高斯分布的，忽略其他的神经元，只考虑输入层到第一个神经元的权重：

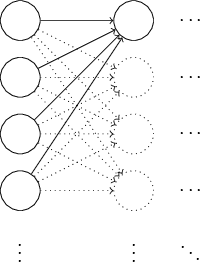
假设我们的输入x一半为1，一半为0，考虑z=$\Sigma$_jw_jx_j+b，z是501项之和：500个输入为1的神经元的权重和一项偏置项。所以z的分布为均值为0，标准差为$\sqrt{501}$ $\approx$ 22.4：

从图中看出z绝对值可能远远大于1，所以sigmoid函数会非常接近1或者0，神经元达到饱和，出现了learning slowdown的问题。由于正态分布太散了，我们尝试把它“挤压”一下，神经元输入权重标准差改为1/$\sqrt{n}$，n就是这个神经元的输入权重个数，也可以用n_in表示。bias与之前一样。

嘿嘿嘿发出目的得逞的笑声~这个时候标准差只有大概1.22，就不容易饱和啦。

继续之前的神经网络，Network[784, 30, 10]【应该都熟悉了吧】，SGD(training_data, 30, 10, 0.1, lmbda = 5.0)，学习率从0.5缓慢的降到0.1。可以看到正确率快了很多：

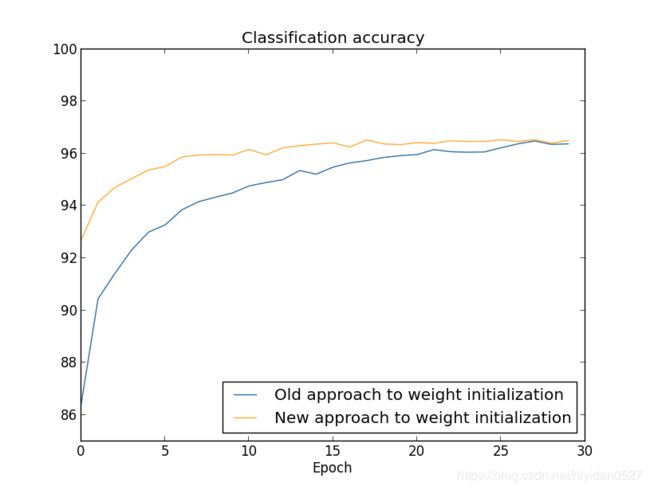
Handwriting recognition revisited

把之前的所有想法（阅读笔记(3)和(4)中的想法）用代码实现一下~在network2.py中

class Network(object):
	def __init__(self, sizes, cost=CrossEntropyCost):
		self.num_layers = len(sizes)
		self.sizes = sizes
		self.default_weight_initializer()
		self.cost=cost

后两行是新加的，首先解释一下default_weight_initializer()

def default_weight_initializer(self):
	self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
	self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]

注意到在bias的时候，我们并没有对第一层神经元初始化任何bias，因为第一层是输入层，所以不会用到bias。除了这个方法，我们还有一个large_weight_initializer方法，使用了第一章的方法：weights&bias分布为N(0,1)

def large_weight_initializer(self):
	self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
	self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]

第二个在Network中的改变是，我们初始化了cost，首先看一下交叉熵损失的定义：

class CrossEntropyCost(object):
	@staticmethod
	def fn(a, y):
		return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a)))
	
	@staticmethod
	def delta(z, a, y):
		return (a-y)

作者选择将交叉熵损失定义成一个类而不是一个函数，是因为损失函数除了衡量实际输出和理想输出之间的差距（CrossEntropyCost.fn），在第二章中后向传播算法还需要我们计算输出误差$\delta$^L，不同的损失函数计算出来是不一样的，对于交叉熵损失函数，之前说过误差为：

这是CrossEntropyCost.delta的作用。对比一下quadratic cost function：

class QuadraticCost(object):
	@staticmethod
	def fn(a, y):
		return 0.5*np.linalg.norm(a-y)*np.linalg.norm(a-y)
	
	@staticmethod
	def delta(z, a, y):
	return (a-y) * sigmoid_prime(z)

除了这些，还有一个很重要的变化就是加了L2正则化，主要就是将正则系数lmbda(SGD方法中)传递到其他的方法中，还有在updata_mini_batch中的两句话：

self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nm for w, nw in zip(self.weights, nabla_w)]
self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)]

还有一个变化是在随机梯度下降方法中加了许多optional flags，为了监控损失和正确率。比如：

net.SGD(training_data, 30, 10, 0.5, lmbda = 5.0, 
	evaluation_data=validation_data, 
	monitor_evaluation_accuracy=True, 
	monitor_evaluation_cost=True, 
	monitor_training_accuracy=True,
	monitor_training_cost=True)

这里就设置validation_data为evaluation_data，有四个flag来监控损失和正确率。

How to choose hyper-parameters

这一节作者讲了如何选择参数，比如学习率、正则化系数等。在完全对问题没有了解的情况下，我们可能选择学习率为10，正则化系数为1000【这都随意
首先我们可以把问题分解，只关注训练集和验证集中的“0”和“1”，只分辨这两个数字，这样一下子就把问题缩小了五倍；还可以训练一个[784, 10]的网络，会比[784, 30, 10]快很多；还可以提高监控的频率，以前是一个周期（50000张）监控一次，现在改成1000张图片监控一次；或者只使用100张验证图片【本来$\lambda$是1000，但是我们训练样本少了，所以为了保证weight decay，$\lambda$改为20.0】：

net = network2.Network([784, 10])
net.SGD(training_data[:1000], 30, 10, 10.0, lmbda = 20.0, evaluation_data=validation_data[:100], monitor_evaluation_accuracy=True)

根据monitor返回的正确率去不断的人为调整这两个参数，正确率高且不断上升，说明调整的方向是正确的，反之则不正确，先确定学习率再确定正则化系数。调整好之后再增加网络复杂性，比如不断增加隐藏层神经元数目。
但是很有可能，不管怎么调整参数，结果都并没有变好，尤其是当网络变复杂之后，不可能再一点一点人为调整。
作者主要针对三个参数介绍设定方法：学习率$\eta$、正则化系数$\lambda$、mini-batch数目。

Learning rate

对于同样的神经网络【之前的30周期、mini-batch数目10、$\lambda$=5.0、训练样本为50000】，我们分别设定学习率为0.025、0.25、2.5：

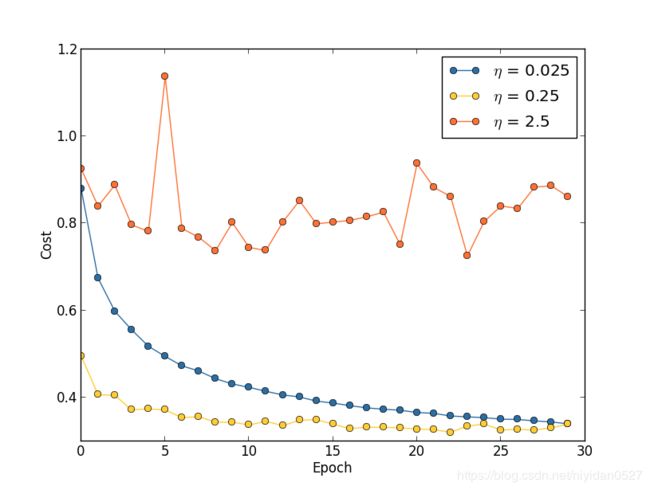
2.5的时候是因为步子太大，错过了最低点，0.25的时候在20个epoch之后饱和了，0.025的时候一直在下降，但是速度较慢。所以更好的方法是前20个epoch选择0.25，之后选择0.025。不过我们先关注如何选择一个单独的好学习率。

这个方法是，首先随机选取一个$\eta$，比如0.01，这个$\eta$可以使cost在刚开始几个epoch立即开始下降，而不是上升或者振动，然后我们尝试0.1，1.0，10.0……等等，直到找到一个$\eta$使cost在刚开始几个epoch振动或者上升。如果刚开始的0.01时损失就开始震动或者上升，那我们就尝试0.001，0.0001……直到找到一个$\eta$使cost在刚开始几个epoch就下降。由此我们找到了一个$\eta$的threshold value。

显然，$\eta$的真实值不能大于这个threshold value。在低于门槛值的情况下，某个$\eta$很好的运行了一段时间，我们可以将其换成更小的值，类似除以2。比如我们选取到的threshold value是0.5，并且0.5运行了超过30个epoch，我们可以使用0.25。

不过用损失来选取参数会导致过拟合问题，之前说过这个问题，我们之后的参数就用validation accuracy来选取。

The regularization parameter $\lambda$

刚开始令$\lambda$为0，选择合适的$\eta$，然后设$\lambda$初值为1.0，然后以10倍增加或减少。等选择了合适的$\lambda$，再反过来重新考虑合适的$\eta$。

mini-batch size

复习一下，mini-batch的主要想法是由于计算所有的训练样本的梯度太复杂，我们选取一小部分样本计算梯度，来代替总梯度。如果样本选少了，很可能代替的不是那么准确，但是作者说问题不大，因为我们的mini-batch可以变，这样子误差就会被平均。
我们可以使用矩阵同时计算mini-batch中所有样本，而不是一遍遍循环计算（书中上一章提过，我没记笔记，即用一个矩阵而不是用很多个向量来代表输入）。我们可以用这个方法去计算有一百个训练样本的mini-batch，可能只需要循环计算50个样本的时间就能完成。比如有100个样本的时候，循环计算的权重变化：

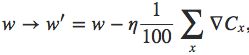
而使用矩阵时的权重变化：

第二种是一种训练方法，叫online learning，指的是每来一个训练样本，就计算一次损失来更新权重，能够根据线上反馈数据，实时进行模型调整。所以这样子就远远比来一百个样本然后统一计算损失再取平均快得多，我们的权重更新频率大大提高。假设我们变化学习率，比如以100倍的速度增加，那我们的权重更新就变成：

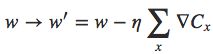
所以，mini-batch越大速度就会越快【其实我这里有点没看懂，是因为权重更新变快所以速度快了吗？截图放下面，有时间复习一下：

mini-batch数量要是少了，就没有充分运用用矩阵计算的快捷简便，要是多了，就没有办法很快的更新权重。mini-batch size是相对独立的一个参数，并不需要跟其他参数一起考虑最优化。正确的做法是，其他的参数用一些合适（并不一定非要最优化）的值，然后试验一系列mini-batch size，然后改变学习率$\eta$。观察验证集正确率和时间（不是epoch），选择学习最快的mini-batch size。然后用这个mini-batch size去选择其他的参数的最优值。

全部代码我自己实现了一下，附在下面供参考

'''network2.py
An improved version of network.py, implementing the stochastic 
gradient descent learning algorithm for a feedforward neural 
network. Improvements include the addition of the cross-entropy 
cost function, regularization, and better initialization of 
network weights. Note that I have focused on making the code 
simple, easily readable, and easily modifiable. It is not 
optimized, and omits many desirable features.
'''

#### Libraries
# Standard library
import json
import random
import sys

# Third-party libraries
import numpy as np

#### Define the quadratic and cross-entropy cost functions

class QuadraticCost(object):

    @staticmethod
    def fn(a, y):
        return 0.5*np.linalg.norm(a-y)**2

    @staticmethod
    def delta(z, a, y):
        return (a-y)*sigmoid_prime(z)

class CrossEntropyCost(object):

    @staticmethod
    def fn(a, y):
        return np.sum(np.nan_to_num(-y*np.log(a)-(1-y)*np.log(1-a)))

    @staticmethod
    def delta(z, a, y):
        return (a-y)

#### Main network class

class Network(object):
    def __init__(self, sizes, cost=CrossEntropyCost):
        self.num_layers = len(sizes)
        self.sizes = sizes
        self.default_weight_initializer()
        self.cost=cost

    def default_weight_initializer(self):
        self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
        self.weights = [np.random.randn(y, x)/np.sqrt(x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]

    def large_weight_initializer(self):
        self.biases = [np.random.randn(y, 1) for y in self.sizes[1:]]
        self.weights = [np.random.randn(y, x) for x, y in zip(self.sizes[:-1], self.sizes[1:])]

    def feedforward(self, a):
        for b, w in zip(self.biases, self.weights):
            a = sigmoid(np.dot(w, a)+b)
        return a

    def SGD(self, training_data, epochs, mini_batch_sizes, eta,
            lmbda=0.0,
            evaluation_data=None,
            monitor_evaluation_cost=False,
            monitor_evaluation_accuracy=False,
            monitor_training_cost=False,
            monitor_training_accuracy=False):
        if evaluation_data:
            n_data = len(evaluation_data)
        n = len(training_data)
        evaluation_cost, evaluation_accuracy = [], []
        training_cost, training_accuracy = [], []
        for j in range(epochs):
            random.shuffle(training_data)
            mini_batches = [
                training_data[k:k+mini_batch_size]
                for k in range(0, n, mini_batch_size)]
            for mini_batch in mini_batches:
                self.update_mini_batch(mini_batch, eta, lmbda, len(training_data))
            print('Epoch %s training complete' % j)
            if monitor_training_cost:
                cost = self.total_cost(training_data, lmbda)
                training_cost.append(cost)
                print("Cost on training data: {}".format(cost))
            if monitor_training_accuracy:
                accuracy = self.accuracy(training_data, convert=True)
                training_accuracy.append(accuracy)
                print("Accuracy on training data: {}/{}".format(accuracy, n))
            if monitor_evaluation_cost:
                cost = self.total_cost(evaluation_data, lmbda, convert=True)
                evaluation_cost.append(cost)
                print("Cost on evaluation data: {}".format(cost))
            if monitor_evaluation_accuracy:
                accuracy = self.accuracy(evaluation_data)
                evaluation_accuracy.append(accuracy)
                print("Accuracy on evaluation data: {}/{}".format(self.accuracy(evaluation_data), n_data))
            print()
        return evaluation_cost, evaluation_accuracy, training_cost, training_accuracy

    def update_mini_batch(self, mini_batch, eta, lmbda, n):
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        for x, y in mini_batch:
            delta_nabla_b, delta_nabla_w = self.backprop(x, y)
            nabla_b = [nb+dnb for nb, dnb in zip(nabla_b, delta_nabla_b)]
            nabla_w = [nw+dnw for nw, dnw in zip(nabla_w, delta_nabla_w)]
        self.weights = [(1-eta*(lmbda/n))*w-(eta/len(mini_batch))*nw for w, nw in zip(self.weights, nabla_w)]
        self.biases = [b-(eta/len(mini_batch))*nb for b, nb in zip(self.biases, nabla_b)]

    def backprop(self, x, y):
        nabla_b = [np.zeros(b.shape) for b in self.biases]
        nabla_w = [np.zeros(w.shape) for w in self.weights]
        # feedforward
        activation = x
        activations = [x]
        zs = []  # list to store all the z vectors
        for b, w in zip(self.biases, self.weights):
            z = np.dot(w, activation)+b
            zs.append(z)
            activation = sigmoid(z)
            activations.append(activation)
        # backward pass
        delta = (self.cost).delta(zs[-1], activations[-1], y)
        nabla_b[-1] = delta
        nabla_w[-1] = np.dot(delta, activations[-2].transpose())
        for l in range(2, self.num_layers):
            z = zs[-1]
            sp = sigmoid_prime(z)
            delta = np.dot(self.weights[-l+1].transpose(), delta)*sp
            nabla_b[-1] = delta
            nabla_w[-1] = np.dot(delta, activations[-l+1].transpose())
        return (nabla_b, nabla_w)

    def accuracy(self, data, convert=False):
        '''The flag "convert" should be set to False if the data 
        set is validation or test data (the usual case), and to 
        True if the data set is the training data. The need for 
        this flag arises due to differences in the way the results 
        "y" are represented in the different data sets.'''
        if convert:
            results = [(np.argmax(self.feedforward(x)), np.argmax(y)) for (x, y) in data]
        else:
            results = [(np.argmax(self.feedforward(x)), y) for (x, y) in data]
        return sum(int(x == y) for (x, y) in results)

    def total_cost(self, data, lmbda, convert=False):
        cost = 0.0
        for x, y in data:
            a = self.feedforward(x)
            if convert:
                y = vectorized_result(y)
                cost += self.cost.fn(a, y)/len(data)
            cost += 0.5*(lmbda/len(data))*sum(np.linalg.norm(w)**2 for w in self.weights)
            return cost

    def save(self, filename):
        data = {"sizes": self.sizes,
                "weights": [w.tolist() for w in self.weights],
                "biases": [b.tolist() for b in self.biases],
                "cost": str(self.cost.__name__)}
        f = open(filename, "w")
        json.dump(data, f)
        f.close()


#### Loading a Network
def load(filename):
    f = open(filename, "r")
    data = json.load(f)
    f.close()
    cost = getattr(sys.modules[__name__], data["cost"])
    net = Network(data["sizes"], cost=cost)
    net.weights = [np.array(w) for w in data["weights"]]
    net.biases = [np.array(b) for b in data["biases"]]
    return net

#### Miscellaneous functions
def vectorized_result(j):
    e = np.zeros((10, 1))
    e[j] = 1.0
    return e

def sigmoid(z):
    return 1.0/(1.0+np.exp(-z))

def sigmoid_prime(z):
    return sigmoid(z)*(1-sigmoid(z))