正则化贪心森林RGF(Regularized Greedy Forest)详解和实战
前言
因为RGF是一针对GBDT缺点而改进的算法,所以在弄清楚之前,你需要了解GBDT算法的原理,包括了解决策树,boosting算法。
一开始接触到RGF的时候,是看了这篇IBM的论文Predicting Disk Replacement towards Reliable Data Centers
里面提到用了RGF的算法去预测硬盘故障,惊艳我的是居然预测precision和recall都到98%以上,并且还可以做到提前预测,所以就觉得RGF 算法很厉害。(虽然我最后复现的时候结果没有论文说的那么高)
1. Boosting算法的简单介绍
Boosting算法是学习多个分类器,并将这些分类器进行线性组合,提高分类性能。整个模型是
y i ^ = ϕ ( x i ) = ∑ k = 1 K f k ( x i ) , f k ϵ F , \hat{y_{i}}=\phi \left ( x_{i} \right )=\sum_{k=1}^{K}f_{k}\left ( x_{i} \right ),f_{k}\epsilon F, yi^=ϕ(xi)=k=1∑Kfk(xi),fkϵF,
在初始化(第0次迭代)的时候呢,模型是:
y ^ i ( 0 ) = 0 \hat{y}_{i}^{(0)}=0 y^i(0)=0
然后接下来每一次迭代都学习一个分类器,再加入模型。第1次迭代:
y ^ i ( 1 ) = f 1 ( x i ) = y ^ i ( 0 ) + f 1 ( x i ) \hat{y}_{i}^{(1)}=f_{1}(x_{i})=\hat{y}_{i}^{(0)}+f_{1}(x_{i}) y^i(1)=f1(xi)=y^i(0)+f1(xi)
第2次迭代:
y ^ i ( 2 ) = f 1 ( x i ) + f 2 ( x i ) = y ^ i ( 1 ) + f 2 ( x i ) \hat{y}_{i}^{(2)}=f_{1}(x_{i})+f_{2}(x_{i})=\hat{y}_{i}^{(1)}+f_{2}(x_{i}) y^i(2)=f1(xi)+f2(xi)=y^i(1)+f2(xi)
第t次迭代:
y ^ i ( t ) = ∑ k = 1 t f k ( x i ) = y ^ i ( t − 1 ) + f t ( x i ) \hat{y}_{i}^{(t)}=\sum_{k=1}^{t}f_{k}\left ( x_{i} \right )=\hat{y}_{i}^{(t-1)}+f_{t}(x_{i}) y^i(t)=k=1∑tfk(xi)=y^i(t−1)+ft(xi)
GBDT就是一个Boosting算法,它由多个回归树(CART)组合起来进行预测的模型。
但是GBDT有不足的地方:
- 每一次的迭代中的唯一目标就是学习出 一颗决策树,从而将单棵树的学习与整个森林的学习分隔开,没有很好地利用决策树本身的性质。新增的决策树只改变了本身的参数而没有改变老树的参数,实际上相当于只做了一个局部的搜索
- 为了避免训练出来过拟合的模型,GBDT需要控制学习步长 s,这种情况可能会造成需要无穷多棵决策树才能很好的完成拟合
为了解决上面的问题,Rie Johnson等在论文Learning Nonlinear Functions Using Regularized Greedy Forest中提出了RGF算法
2. RGF介绍
RGF的是Regularized Greedy Forest的缩写,全称是正则化贪心森林RGF。
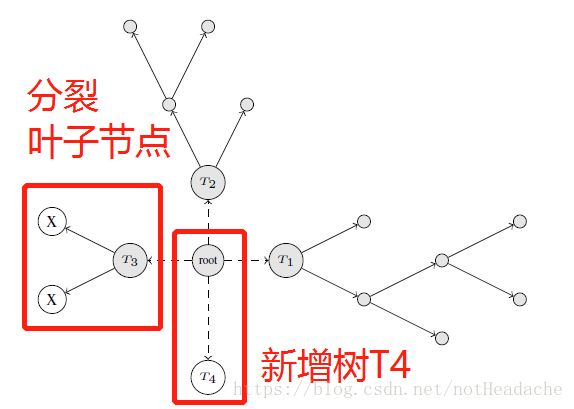
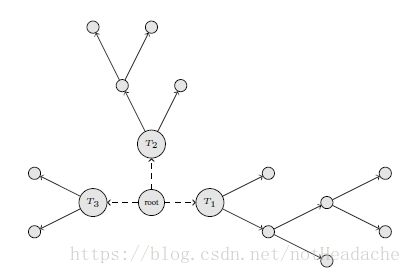
RGF是一种决策森林,由多棵决策树݈组合而成,如下图所示,就是一个三颗决策树组成的决策森林。
RGF的特点是(和GBDT的不同)
- 每次迭代直接对整个决策森林进行学习
- 新增树后进行全局的参数优化
- 引入针对决策树的正则项来防止过拟合
接下来我们详细说一下RGF是如何做到的。
2.1 决策树种的节点的表示 b v ( x ) b_{v}(x) bv(x)
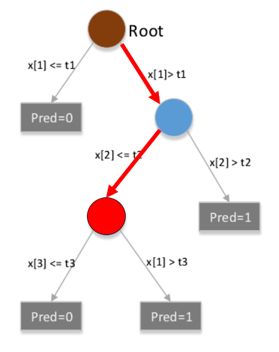
在一颗决策树中,样本从根节点到子节点(不管是叶子节点还是非叶子节点)的这样一条路径就形成了一条分类规则,所以对于决策树的一个子节点 v v v来说,有一个公式可以描述从根节点到这个子节点 v v v的这个规则:
b v ( x ) = ∏ j I ( x [ i j ] ≤ t j ) ∏ k I ( x [ i k ] > t k ) b_{v}(x)=\prod _{j}I(x[i_{j}]\leq t_{j})\prod _{k}I(x[i_{k}]>t_{k}) bv(x)=j∏I(x[ij]≤tj)k∏I(x[ik]>tk)
- 这里先好好解释一下这个公式,因为在看第一眼的时候并不是很理解这个公式。
- 函数 I ( x ) I(x) I(x)表示当括号中为真时结果为 1,否则为 0。
- 如果 b v ( x ) = 1 b_{v}(x)=1 bv(x)=1说明 x x x经过决策树节点的判断,能够到达 v v v这个节点。反之,则到达不了。
- 一个样本从根节点到子节点的过程中,在每个非叶子节点处都进行某个特征维度的值的二元测试(不是大于阈值就是小于阈值),在经过的全部非叶子节点处的测试中,有 j j j个测试满足的是小于当前非叶子节点出的阈值的条件,有 k k k个满足的是大于当前非叶子节点出的阈值条件。
- 如下图所示,在从根节点到红色节点的这个红色的路径中,在根节点这里有一个判断是大于根节点的阈值,在蓝色的节点这里有一个判断是小于等于蓝色节点的阈值。所以红色这个节点可以用这个公式来表示: b v ( x ) = I ( x [ 2 ] ≤ t 2 ) I ( x [ 1 ] > t 1 ) b_{v}(x)=I(x[2]\leq t_{2})I(x[1]>t_{1}) bv(x)=I(x[2]≤t2)I(x[1]>t1)
于是在决策树里面每一个节点 v v v(叶子节点和非叶子节点)都可以由 b v ( x ) b_{v}(x) bv(x)来表示。
2.2 决策深林的表示
于是,单棵决策树中,每个有着 v 1 , v 2 v_{1},v_{2} v1,v2两个子节点的节点 v v v,都可以表示为子节点的组合 b v ( x ) = b v 1 ( x ) + b v 2 ( x ) b_{v}(x)=b_{v1}(x)+b_{v2}(x) bv(x)=bv1(x)+bv2(x)
决策森林模型可以看成是叶节点的组合模型,而不是决策树模型的组合 h F ( x ) = ∑ v ϵ F a v b v ( x ) h_{F}(x)=\sum _{v\epsilon F}a_{v}b_{v}(x) hF(x)=vϵF∑avbv(x)
- 当 v v v不是叶子节点的时候, a v = 0 a_{v}=0 av=0
- a v a_{v} av表示节点的权重参数
- F F F表示决策森林
有了决策森林模型的叶子组合模型的表示,RGF 算法可以直接利用森林的结构直接学习贪心森林而不是每次迭代的时候只是生成单颗决策树加入决策森林。
2.3 损失函数
RGF定义一个损失函数 L R ( F ) L_{R}(F) LR(F)来构建这个决策森林:
L R ( F ) = L ( h F ( x ) , Y ) + R ( h F ) L_{R}(F)=L(h_{F}(x),Y)+R(h_{F}) LR(F)=L(hF(x),Y)+R(hF)
- R ( h F ) R(h_{F}) R(hF)是正则化项
损失函数 L ( h F ( x ) , Y ) L(h_{F}(x),Y) L(hF(x),Y)必须根据处理的问题来进行定义,例如针对线性回归问题,损失函数定义为平方损失函数 L ( h F ( x ) , Y ) = ∑ i = 1 n ( h ( x i ) − y i ) 2 L(h_{F}(x),Y)=\sum_{i=1}^{n}(h(x_{i})-y_{i})^{2} L(hF(x),Y)=i=1∑n(h(xi)−yi)2
针对二分类问题可以定义为逻辑损失函数 L ( h F ( x ) , Y ) = ∑ i = 1 n l n ( 1 + e − h ( x i ) y i ) L(h_{F}(x),Y)=\sum_{i=1}^{n}ln(1+e^{^{-h(x_{i})y_{i}}}) L(hF(x),Y)=i=1∑nln(1+e−h(xi)yi)
2.4 RGF算法
有了损失函数,我们接下来的一步就是如何得出RGF的决策森林。
RGF在每一次迭代学习的时候,直接对整个决策森林进行学习,而不是只学习新增的决策树。于是,每次迭代:
- 在固定所有节点权重的前提下,对整个决策森林的叶节点执行贪心搜索,不断循环评估找到使得损失函数下降最快的结构变化,并执行相应的结构变化操作获得最优的森林结构,然后执行2
- 固定森林的结构,更新节点权重 a v a_{v} av最小化损失函数。因为现在决策森林是用 h F ( x ) = ∑ v ϵ F a v b v ( x ) h_{F}(x)=\sum _{v\epsilon F}a_{v}b_{v}(x) hF(x)=∑vϵFavbv(x)来表示,所RGF固定森林的结构 b v ( x ) b_{v}(x) bv(x),更新节点的权重 a v a_{v} av
在步骤1中,为了获得最优的森林结构,可以执行以下两种方式的一种,取决于那种可以使得损失函数最小:
- 分裂一个已有的叶子节点
- 在森林中新建一个决策树分支
更多算法的细节请看RGF的论文,比如:
- 参数 a v a_{v} av的优化算法:牛顿法
3. RGF实战
Github上有一个RGF的python使用:https://github.com/RGF-team/rgf/tree/master/python-package
首先通过
pip install rgf_python
进行安装RGF
然后就可以通过导入RGF的包进行使用了
from rgf.sklearn import RGFClassifier
用鸢尾花卉数据集进行试验
from sklearn import datasets
from sklearn.utils.validation import check_random_state
from sklearn.model_selection import StratifiedKFold, cross_val_score
from rgf.sklearn import RGFClassifier
iris = datasets.load_iris()
rng = check_random_state(0)
perm = rng.permutation(iris.target.size)
iris.data = iris.data[perm]
iris.target = iris.target[perm]
rgf = RGFClassifier(max_leaf=400,
algorithm="RGF_Sib",
test_interval=100,
verbose=True)
n_folds = 3
rgf_scores = cross_val_score(rgf,
iris.data,
iris.target,
cv=StratifiedKFold(n_folds))
rgf_score = sum(rgf_scores)/n_folds
print('RGF Classifier score: {0:.5f}'.format(rgf_score))
RGF参数选择:
ALGORITHMS = (“RGF”, “RGF_Opt”, “RGF_Sib”)
LOSSES = (“LS”, “Expo”, “Log”, “Abs”)
可以选择正则化的算法和损失函数:
rgf = RGFClassifier(max_leaf=400,
algorithm="RGF_Sib",
loss="Expo"
test_interval=100,
verbose=True)
其中:
Loss function.
LS: Square loss.
Expo: Exponential loss.
Log: Logistic loss.
Abs: Absolute error loss.
Regularization algorithm.
RGF: RGF with L2 regularization on leaf-only models.
RGF Opt: RGF with min-penalty regularization.
RGF Sib: RGF with min-penalty regularization with the sum-to-zero sibling constraints.