李宏毅学习笔记22.Ensemble
文章目录
- 前言
- 概述(Game alert)
- Bagging
- 决策树(秒讲)
- 决策树实例(二次元版)
- 随机森林
- Boosting
- Boosting框架
- Adaboost
- How to find a new training set that fails $f_1(x)$?
- 求d1(数学推导)
- Adaboost算法
- Adaboost Toy Example
- AdaBoost证明(Warning of Math)
- AdaBoost结果分析
- AdaBoost+决策树实例
- Gradient Boosting
- Stacking
前言
ensemble的目的是为了训练出几个“好而不同”的子模型,希望起到三个臭皮匠胜过一个诸葛亮的作用。本节讲了两种集成的构架:bagging和boosting。重点对boosting的最经典算法AdaBoost进行讲解,给出了实例,最后还进行了数学证明。
公式输入请参考:在线Latex公式
概述(Game alert)

diverse:分散;aggregate:集合
Ensemble:群殴,有两种方式:Bagging和Boosting
Bagging
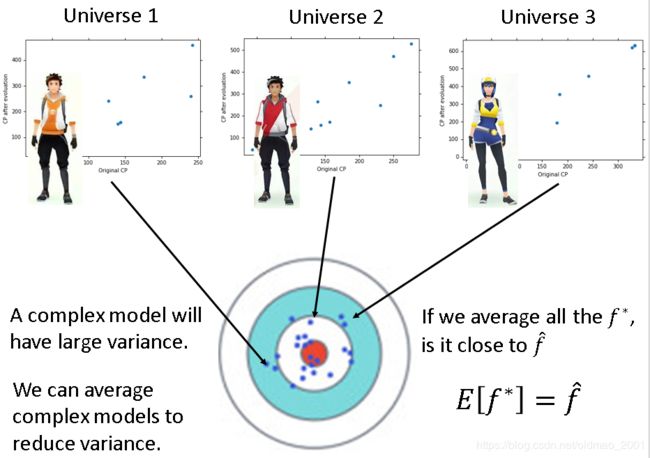
这个是之前讲bias和variance的内容,这里减少variance的方法是用多个模型求平均的方式,这个也算是bagging的思想,但是不是用多个模型,而是从数据上下手,但是为了确保这个模型在不一样的同时也要足够优秀。
支书语录:集成模型的目的是为了训练出几个“好而不同”的子模型,希望起到三个臭皮匠胜过一个诸葛亮的作用,那么为了使各个模型有差异,一种做法是用不同的模型,还有一种做法是给不一样的训练数据,但是为了确保这个模型在不一样的同时也要足够优秀,就要使得各个模型拿到的数据量也是相同的,于是就会进行有放回抽样,这样每个子模型在训练数据上就会有差异,但是做的习题量还是一样的。
假设我们有N笔数据,则对这N笔数据进行放回抽样sampling with replacement,每次取1笔数据(取完放回去),取N’(一般N’=N)次后组成新的data set,每个data set里面的数据都是不一样的。

然后每个data set都去做learning,得到若干个function(这里是四个);测试的时候,将testing data放入四个function中,得到四个输出y,然后将多个y进行平均(regression的时候)或求voting(classification的时候)。
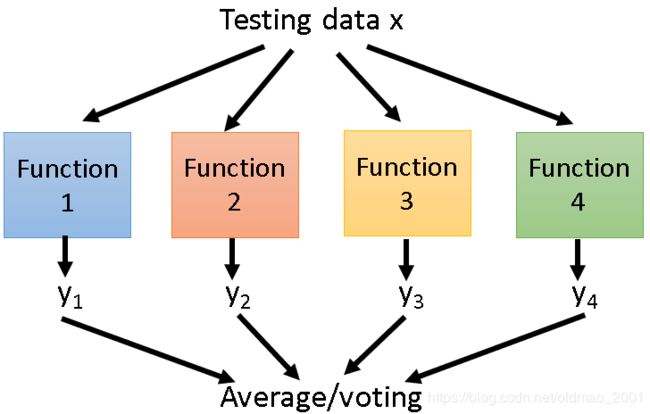
这样做会降低variance,不容易overfitting。
使用bagging的时机:当模型比较复杂,担心过拟合的时候,例如决策树(很深的)。
带bagging的decision tree就是随机森林。
决策树(秒讲)
假设每一个对象x有两个feature组成的向量 [ x 1 x 2 ] \begin{bmatrix} x_1\\ x_2 \end{bmatrix} [x1x2]。决策树就是根据training data建立一棵树:
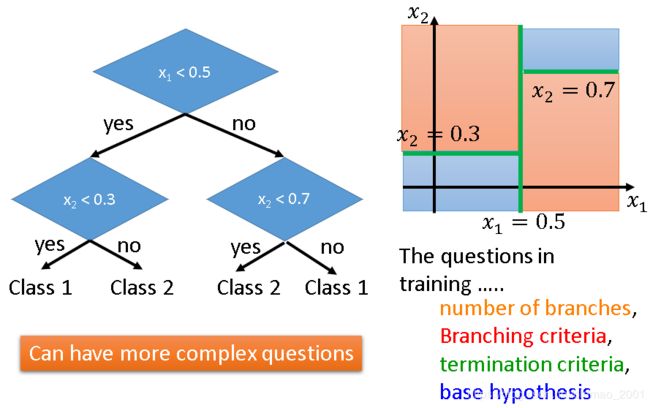
建立过程中需要考虑的问题包括:分支的数量、分支的条件、停止分支的条件、问题的集合等。
决策树实例(二次元版)
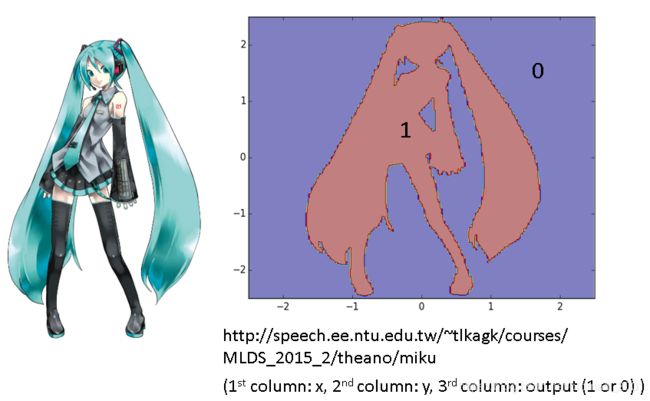
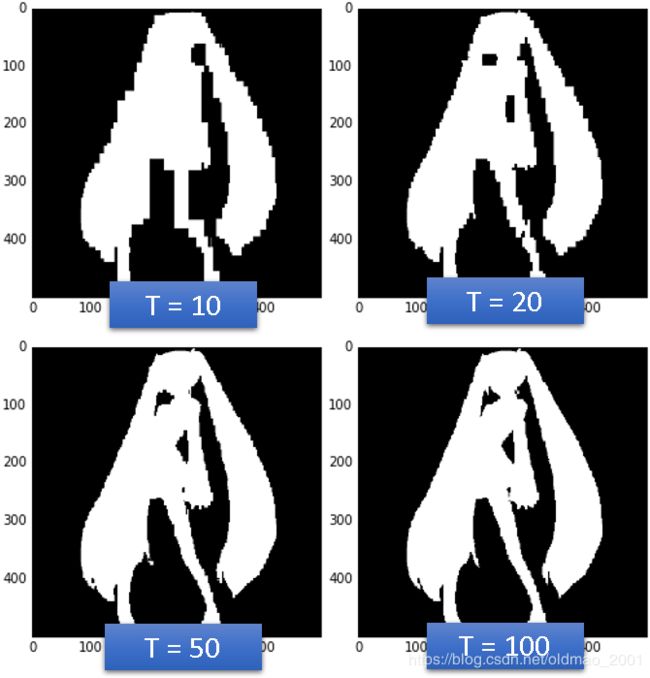
要分类的数据分布如上图所示,下载链接也有:二次元数据集。实验结果:
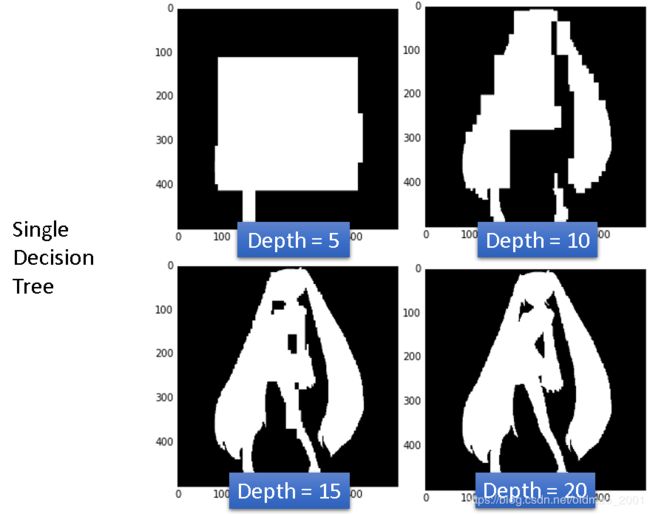
结论是:只要数够深,每个data都可以作为一个节点,所以决策树可以做到training error rate为0。也就是单颗决策树容易overfitting,因此产生了随机森林(Random Forest)
随机森林
Decision tree:
Easy to achieve 0% error rate on training data
If each training example has its own leaf ……
Random forest本质就是Bagging of decision tree
Resampling training data is not sufficient
Randomly restrict the features/questions used in each split
还有一种叫Out-of-bag validation for bagging。
之前在机器学习中有一个技巧叫cross validation,这个Out-of-bag validation for bagging自带这个属性,就是说每个function在训练的时候只用到部分data,例如现在我们有 x 1 x^1 x1、 x 2 x^2 x2、 x 3 x^3 x3、 x 4 x^4 x4四笔数据, f 1 f_1 f1只用 x 1 x^1 x1、 x 2 x^2 x2进行训练,以此类推。
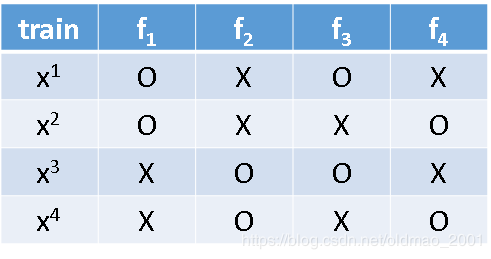
相当于用 f 2 f_2 f2和 f 4 f_4 f4bagging的结果去test x 1 x^1 x1,即:
Using RF = f 2 f_2 f2+ f 4 f_4 f4 to test x 1 x^1 x1,同理有:
Using RF = f 2 f_2 f2+ f 3 f_3 f3 to test x 2 x^2 x2,
Using RF = f 1 f_1 f1+ f 4 f_4 f4 to test x 3 x^3 x3,
Using RF = f 1 f_1 f1+ f 3 f_3 f3 to test x 4 x^4 x4。
最后把 x 1 x^1 x1、 x 2 x^2 x2、 x 3 x^3 x3、 x 4 x^4 x4求平均error得到一个Out-of-bag (OOB) error。
虽然没有切分validation set,但是function在训练的时候并没哟看过所有的training data。
接下来看下随机森林的二次元分类的结果:(100颗树)

Boosting
主要作用:Improving Weak Classifiers
炸天的保证:
If your ML algorithm can produce classifier with error rate smaller than 50% on training data, you can obtain 0% error rate classifier after boosting.
如果你的分类模型有50%以下的错误率,那么Boosting可以帮你的分类模型达到0%的错误率。
Boosting框架

蓝字部分需要注意,这里和前面的bagging不同的,Boosting是有顺序的。
假设我们有如下数据:

我们如何获得不同的分类器呢?还是和bagging的开始的思想一样,就在在不同的训练集数据中训练。获取不同训练数据集有两种方式:
Re-sampling your training data to form a new set
Re-weighting your training data to form a new set
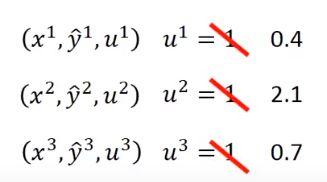
从可以看到改变权重可以得到不同的训练集,其实resampling本质上也一样,例如x1被抽到两次和把x1对应的权重改成2是一样的效果。
In real implementation, you only have to change the cost/objective function,例如原来的损失函数为:
L ( f ) = ∑ n l ( f ( x n ) , y ^ n ) L(f)=\sum_nl(f(x^n),\widehat y^n) L(f)=n∑l(f(xn),y n)
加上权重后,损失函数变为:
L ( f ) = ∑ n u n l ( f ( x n ) , y ^ n ) L(f)=\sum_nu^nl(f(x^n),\widehat y^n) L(f)=n∑unl(f(xn),y n)
就是每个 f ( x n ) f(x^n) f(xn)都乘上权重 u n u^n un,意味某个数据的权重大些,那么在计算损失函数中考虑得就多些。由此引出了boost众多方法中最经典的一种:
Adaboost
思路:
先训练一个function f 1 ( x ) f_1(x) f1(x)
找一组新的traning data来训练 f 2 ( x ) f_2(x) f2(x),这组新的traning data的特点是,如果把它拿给 f 1 ( x ) f_1(x) f1(x)训练, f 1 ( x ) f_1(x) f1(x)的错误率在50%以上。
How to find a new training set that fails f 1 ( x ) f_1(x) f1(x)?
先看 f 1 ( x ) f_1(x) f1(x)在training data上的error rate如何计算,假设 ϵ 1 \epsilon_1 ϵ1是 f 1 ( x ) f_1(x) f1(x)在training data上的error rate,则有:
ϵ 1 = ∑ n u 1 n δ ( f 1 ( x n ) < > y ^ n ) Z 1 Z 1 = ∑ n u 1 n ϵ 1 < 0.5 \epsilon_1=\frac{\sum_nu_1^n\delta(f_1(x^n)<>\widehat y^n)}{Z_1} \quad Z_1=\sum_nu_1^n \quad \epsilon_1<0.5 ϵ1=Z1∑nu1nδ(f1(xn)<>y n)Z1=n∑u1nϵ1<0.5
除以 Z 1 Z_1 Z1代表归一化,因为上面乘了权重 u 1 n u_1^n u1n.,另外如果 ϵ 1 > 0.5 \epsilon_1>0.5 ϵ1>0.5可以把分类翻转一下。
将权重从 u 1 n u_1^n u1n.改到 u 2 n u_2^n u2n.,使得:
∑ n u 2 n δ ( f 1 ( x n ) < > y ^ n ) Z 2 = 0.5 \frac{\sum_nu_2^n\delta(f_1(x^n)<>\widehat y^n)}{Z_2}=0.5 Z2∑nu2nδ(f1(xn)<>y n)=0.5
f 1 ( x ) f_1(x) f1(x)在 u 2 n u_2^n u2n.的数据集上的表现是随机的
然后在 u 2 n u_2^n u2n.的数据集上训练 f 2 ( x ) f_2(x) f2(x),得到的 f 2 ( x ) f_2(x) f2(x)与 f 1 ( x ) f_1(x) f1(x)是互补的。看不懂没关系,看实例:
假设有四笔training data,他们的权重都为1:
( x 1 , y ^ 1 , u 1 ) u 1 = 1 (x^1,\widehat y^1,u^1)\quad u^1=1 (x1,y 1,u1)u1=1
( x 2 , y ^ 2 , u 2 ) u 2 = 1 (x^2,\widehat y^2,u^2)\quad u^2=1 (x2,y 2,u2)u2=1
( x 3 , y ^ 3 , u 3 ) u 3 = 1 (x^3,\widehat y^3,u^3)\quad u^3=1 (x3,y 3,u3)u3=1
( x 4 , y ^ 4 , u 4 ) u 4 = 1 (x^4,\widehat y^4,u^4)\quad u^4=1 (x4,y 4,u4)u4=1
把他们丢入分类器 f 1 ( x ) f_1(x) f1(x)中,由于 f 1 ( x ) f_1(x) f1(x)不是很强,所以它会分错,这里假设它把第二笔数据分错了
( x 1 , y ^ 1 , u 1 ) u 1 = 1 正 确 (x^1,\widehat y^1,u^1)\quad u^1=1\quad 正确 (x1,y 1,u1)u1=1正确
( x 2 , y ^ 2 , u 2 ) u 2 = 1 错 误 (x^2,\widehat y^2,u^2)\quad u^2=1\quad 错误 (x2,y 2,u2)u2=1错误
( x 3 , y ^ 3 , u 3 ) u 3 = 1 正 确 (x^3,\widehat y^3,u^3)\quad u^3=1\quad 正确 (x3,y 3,u3)u3=1正确
( x 4 , y ^ 4 , u 4 ) u 4 = 1 正 确 (x^4,\widehat y^4,u^4)\quad u^4=1\quad 正确 (x4,y 4,u4)u4=1正确
则 f 1 ( x ) f_1(x) f1(x)在这四笔数据上的error rate为 ϵ 1 = 0.25 \epsilon_1=0.25 ϵ1=0.25(错一道对三道),接下来要改变weight,就是把u的值变一下,使得 ϵ 1 \epsilon_1 ϵ1变大,原则就是让分类正确的权重变小,分类错误的权重变大:
( x 1 , y ^ 1 , u 1 ) u 1 = 1 3 正 确 (x^1,\widehat y^1,u^1)\quad u^1=\frac{1}{\sqrt3}\quad 正确 (x1,y 1,u1)u1=31正确
( x 2 , y ^ 2 , u 2 ) u 2 = 3 错 误 (x^2,\widehat y^2,u^2)\quad u^2=\sqrt3\quad 错误 (x2,y 2,u2)u2=3错误
( x 3 , y ^ 3 , u 3 ) u 3 = 1 3 正 确 (x^3,\widehat y^3,u^3)\quad u^3=\frac{1}{\sqrt3}\quad 正确 (x3,y 3,u3)u3=31正确
( x 4 , y ^ 4 , u 4 ) u 4 = 1 3 正 确 (x^4,\widehat y^4,u^4)\quad u^4=\frac{1}{\sqrt3}\quad 正确 (x4,y 4,u4)u4=31正确
这个时候的 ϵ 1 = 3 3 + 1 3 + 1 3 + 1 3 = 0.5 \epsilon_1=\frac{\sqrt3}{\sqrt3+\frac{1}{\sqrt3}+\frac{1}{\sqrt3}+\frac{1}{\sqrt3}}=0.5 ϵ1=3+31+31+313=0.5,这个时候用上面新的u来训练 f 2 ( x ) f_2(x) f2(x), f 2 ( x ) f_2(x) f2(x)可以根据新的u得到 ϵ 2 < 0.5 \epsilon_2<0.5 ϵ2<0.5。
.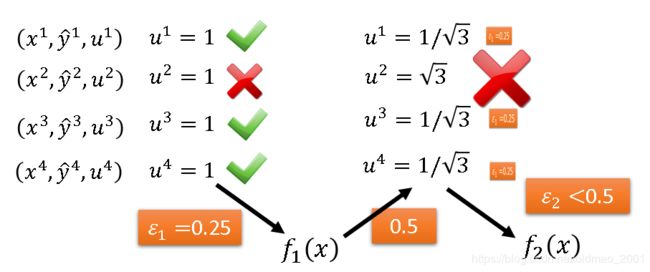
总结改变weight的操作如下,其中 d 1 > 1 d_1>1 d1>1,也就是思想是分类错误的数据权重乘以 d 1 > 1 d_1>1 d1>1增加,分类正确的数据权重除以 d 1 > 1 d_1>1 d1>1减少。

求d1(数学推导)
先把 ϵ 1 \epsilon_1 ϵ1的表达式copy下来:
(1) ϵ 1 = ∑ n u 1 n δ ( f 1 ( x n ) < > y ^ n ) Z 1 Z 1 = ∑ n u 1 n \epsilon_1=\frac{\sum_nu_1^n\delta(f_1(x^n)<>\widehat y^n)}{Z_1} \quad Z_1=\sum_nu_1^n \tag{1} ϵ1=Z1∑nu1nδ(f1(xn)<>y n)Z1=n∑u1n(1)
我们希望把公式(1)中的 u 1 n u_1^n u1n替换为u_2^n后weight的值为0.5,即:
(2) ∑ n u 2 n δ ( f 1 ( x n ) < > y ^ n ) Z 2 = 0.5 \frac{\sum_nu_2^n\delta(f_1(x^n)<>\widehat y^n)}{Z_2}=0.5 \tag{2} Z2∑nu2nδ(f1(xn)<>y n)=0.5(2)
根据上面一张图我们还有两个原则:
1、 f 1 ( x n ) < > y ^ n f_1(x^n)<>\widehat y^n f1(xn)<>y n的时候, u 2 n = u 1 n × d 1 u_2^n=u_1^n×d_1 u2n=u1n×d1
2、 f 1 ( x n ) = y ^ n f_1(x^n)=\widehat y^n f1(xn)=y n的时候, u 2 n = u 1 n / d 1 u_2^n=u_1^n/d_1 u2n=u1n/d1
在公式(2)中,分子中的 f 1 ( x n ) f_1(x^n) f1(xn)是不等于 y ^ n \widehat y^n y n的,所以,公式(2)的分子可以写为:
∑ n u 2 n δ ( f 1 ( x n ) < > y ^ n ) = ∑ f 1 ( x n ) < > y ^ n u 1 n × d 1 {\sum_nu_2^n\delta(f_1(x^n)<>\widehat y^n)}=\sum_{f_1(x^n)<>\widehat y^n}u_1^n×d_1 n∑u2nδ(f1(xn)<>y n)=f1(xn)<>y n∑u1n×d1
公式(2)的分母可以写为:
Z 2 = ∑ n u 2 n = ∑ f 1 ( x n ) < > y ^ n u 2 n + ∑ f 1 ( x n ) = y ^ n u 2 n = ∑ f 1 ( x n ) < > y ^ n u 1 n × d 1 + ∑ f 1 ( x n ) = y ^ n u 1 n / d 1 Z_2=\sum_{n}u_2^n=\sum_{f_1(x^n)<>\widehat y^n}u_2^n+\sum_{f_1(x^n)=\widehat y^n}u_2^n=\sum_{f_1(x^n)<>\widehat y^n}u_1^n×d_1+\sum_{f_1(x^n)=\widehat y^n}u_1^n/d_1 Z2=n∑u2n=f1(xn)<>y n∑u2n+f1(xn)=y n∑u2n=f1(xn)<>y n∑u1n×d1+f1(xn)=y n∑u1n/d1
整理后公式(2)变成:
(3) ∑ f 1 ( x n ) < > y ^ n u 1 n × d 1 ∑ f 1 ( x n ) < > y ^ n u 1 n × d 1 + ∑ f 1 ( x n ) = y ^ n u 1 n / d 1 = 0.5 \frac{\sum_{f_1(x^n)<>\widehat y^n}u_1^n×d_1}{\sum_{f_1(x^n)<>\widehat y^n}u_1^n×d_1+\sum_{f_1(x^n)=\widehat y^n}u_1^n/d_1}=0.5\tag{3} ∑f1(xn)<>y nu1n×d1+∑f1(xn)=y nu1n/d1∑f1(xn)<>y nu1n×d1=0.5(3)
把公式(3)等号两边同时取倒数:
(4) ∑ f 1 ( x n ) < > y ^ n u 1 n × d 1 + ∑ f 1 ( x n ) = y ^ n u 1 n / d 1 ∑ f 1 ( x n ) < > y ^ n u 1 n × d 1 = 2 \frac{\sum_{f_1(x^n)<>\widehat y^n}u_1^n×d_1+\sum_{f_1(x^n)=\widehat y^n}u_1^n/d_1}{\sum_{f_1(x^n)<>\widehat y^n}u_1^n×d_1}=2\tag{4} ∑f1(xn)<>y nu1n×d1∑f1(xn)<>y nu1n×d1+∑f1(xn)=y nu1n/d1=2(4)
公式(4)中的分子左边和分母相同,因此消掉这项后变成:
(5) ∑ f 1 ( x n ) = y ^ n u 1 n / d 1 ∑ f 1 ( x n ) < > y ^ n u 1 n × d 1 = 1 \frac{\sum_{f_1(x^n)=\widehat y^n}u_1^n/d_1}{\sum_{f_1(x^n)<>\widehat y^n}u_1^n×d_1}=1\tag{5} ∑f1(xn)<>y nu1n×d1∑f1(xn)=y nu1n/d1=1(5)
也就是:
(6) ∑ f 1 ( x n ) = y ^ n u 1 n / d 1 = ∑ f 1 ( x n ) < > y ^ n u 1 n × d 1 {\sum_{f_1(x^n)=\widehat y^n}u_1^n/d_1}=\sum_{f_1(x^n)<>\widehat y^n}u_1^n×d_1\tag{6} f1(xn)=y n∑u1n/d1=f1(xn)<>y n∑u1n×d1(6)
把公式(6)中左右两边的 d 1 d_1 d1提出来:
(7) 1 d 1 ∑ f 1 ( x n ) = y ^ n u 1 n = d 1 ∑ f 1 ( x n ) < > y ^ n u 1 n \frac{1}{d_1}{\sum_{f_1(x^n)=\widehat y^n}u_1^n}=d_1\sum_{f_1(x^n)<>\widehat y^n}u_1^n\tag{7} d11f1(xn)=y n∑u1n=d1f1(xn)<>y n∑u1n(7)
把公式(1)变一下,把 u 1 n u_1^n u1n提出来:
(8) ϵ 1 = ∑ f 1 ( x n ) < > y ^ n u 1 n Z 1 \epsilon_1=\frac{\sum_{f_1(x^n)<>\widehat y^n}u_1^n}{Z_1} \tag{8} ϵ1=Z1∑f1(xn)<>y nu1n(8)
把公式(8)移项:
(9) ∑ f 1 ( x n ) < > y ^ n u 1 n = Z 1 ϵ 1 {\sum_{f_1(x^n)<>\widehat y^n}u_1^n}={Z_1} \epsilon_1\tag{9} f1(xn)<>y n∑u1n=Z1ϵ1(9)
对于 f 1 ( x n ) = y ^ n f_1(x^n)=\widehat y^n f1(xn)=y n部分,则有:
(10) ∑ f 1 ( x n ) = y ^ n u 1 n = Z 1 ( 1 − ϵ 1 ) {\sum_{f_1(x^n)=\widehat y^n}u_1^n}={Z_1} (1-\epsilon_1)\tag{10} f1(xn)=y n∑u1n=Z1(1−ϵ1)(10)
公式(9)、(10)带入公式(7)的左、右两边,得:
Z 1 ( 1 − ϵ 1 ) / d 1 = Z 1 ϵ 1 d 1 Z_1(1-\epsilon_1)/d_1=Z_1\epsilon_1d_1 Z1(1−ϵ1)/d1=Z1ϵ1d1
最后算出: d 1 = ( 1 − ϵ 1 ) / ϵ 1 > 1 d_1=\sqrt{(1-\epsilon_1)/\epsilon_1}>1 d1=(1−ϵ1)/ϵ1>1大于1是因为 ϵ 1 < 0.5 \epsilon_1<0.5 ϵ1<0.5
Adaboost算法
上面的公式推导之后,下面就简单了,直接上ppt截图

红框部分有点绕, d t = ( 1 − ϵ t ) / ϵ t d_t=\sqrt{(1-\epsilon_t)/\epsilon_t} dt=(1−ϵt)/ϵt与 α t = l n ( 1 − ϵ t ) / ϵ t \alpha_t=ln\sqrt{(1-\epsilon_t)/\epsilon_t} αt=ln(1−ϵt)/ϵt等价,这样就可以把两个表达式写成一个(最下面那个)。
当 f t ( x n ) = y ^ n f_t(x^n)=\widehat y^n ft(xn)=y n的时候 y ^ n f t ( x n ) = 1 \widehat y^nf_t(x^n)=1 y nft(xn)=1;
当 f t ( x n ) < > y ^ n f_t(x^n)<>\widehat y^n ft(xn)<>y n的时候 y ^ n f t ( x n ) = − 1 \widehat y^nf_t(x^n)=-1 y nft(xn)=−1;
经过刚才的步骤,得到一把分类器function: f 1 ( x n ) , f 2 ( x n ) , . . . f t ( x n ) , . . . , f T ( x n ) f_1(x^n),f_2(x^n),...f_t(x^n),...,f_T(x^n) f1(xn),f2(xn),...ft(xn),...,fT(xn)
如何整合aggregate这些分类器?
Uniform weight:方式: H ( x ) = s i g n ( ∑ t = 1 T f t ( x ) ) H(x)=sign(\sum_{t=1}^Tf_t(x)) H(x)=sign(∑t=1Tft(x)),这里面的分类器有好有坏,直接平均不太妥
Non-uniform weight方式: H ( x ) = s i g n ( ∑ t = 1 T α t f t ( x ) ) H(x)=sign(\sum_{t=1}^T\alpha _tf_t(x)) H(x)=sign(∑t=1Tαtft(x)),这里吧分类器乘上权重,结果会好些。Smaller error _, larger weight for final voting.
α t \alpha _t αt咋上图红框中有摆出来公式,来通过实例看下它的具体含义,根据公式:
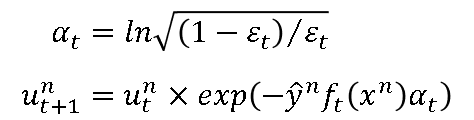
当 ϵ t = 0.1 \epsilon_t=0.1 ϵt=0.1时,错误率较低,分类器很好,根据公式 α t = 1.10 \alpha _t=1.10 αt=1.10, α t \alpha _t αt比较大;
当 ϵ t = 0.4 \epsilon_t=0.4 ϵt=0.4时,错误率较高,分类器很烂,根据公式 α t = 0.2 \alpha _t=0.2 αt=0.2, α t \alpha _t αt比较小。
Adaboost Toy Example
这里例子非常直观,三个迭代就完成了分类,计算就不赘述了,直接套的公式。要分类的数据如下图所示,共有十个点,5个﹢实例,5个﹣实例。总共迭代三次,T=3。
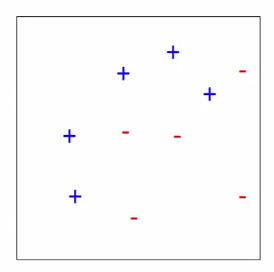
第一次迭代:t=1,初始权重都为1

使用简单分类器 f 1 ( x ) f_1(x) f1(x)在如下图左侧所示位置进行分类,左边为正分类,右边为负分类,右边有三个错误分类点(红色圈圈里面的),带公式计算出三个参数,然后计算出新权重(如下图右边所示)
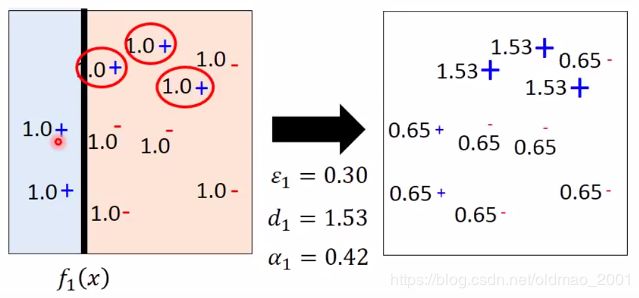
同理,用 f 2 ( x ) f_2(x) f2(x)进行分类,t=2:
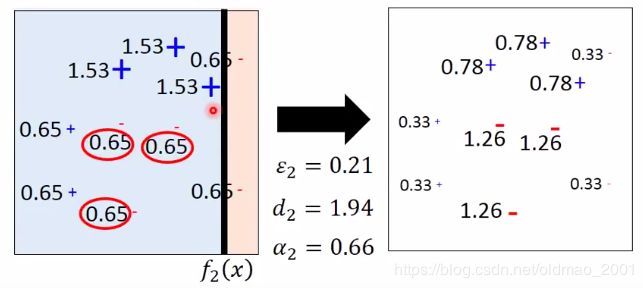
最后用 f 3 ( x ) f_3(x) f3(x)进行分类,t=3,说好只迭代三次,所以迭代结束:
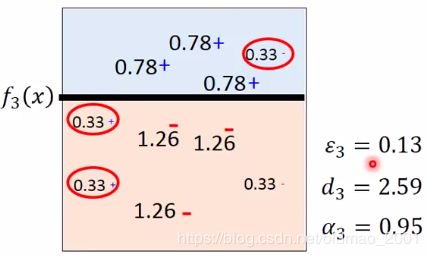
接下来就是三个分类器的组合,虽然刚才三个分类器在分类的时候没有哪个分类器能够完全分类正确,但是组合之后是什么情况?组合的时候要乘上每次迭代的权重 α t \alpha_t αt

三个分类器组合后的形状如下,把整个平面切成了六份:
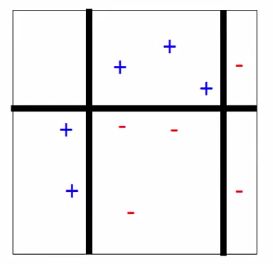
分类结果如下:
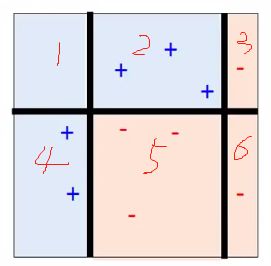
为了讲解方便,我手工添加了编号,例如1号区域,三个分类器都认为应该是蓝色,所以1号区域就是蓝色;2号区域 f 1 ( x ) f_1(x) f1(x)认为是黄色, f 2 ( x ) f_2(x) f2(x)和 f 3 ( x ) f_3(x) f3(x)认为是蓝色且权重加起来比 f 1 ( x ) f_1(x) f1(x)要大,所以2号区域就是蓝色。以此类推。
AdaBoost证明(Warning of Math)
算法简要回顾:AdaBoost算法中的终极分类器由若干个弱分类器 f t ( x ) f_t(x) ft(x)组成,每个分类器 f t ( x ) f_t(x) ft(x)进行分类的错误率为 ϵ t \epsilon_t ϵt,终极分类的分类结果如下:
(11) H ( x ) = s i g n ( ∑ t = 1 T α t f t ( x ) ) H(x)=sign(\sum_{t=1}^T\alpha _tf_t(x))\tag{11} H(x)=sign(t=1∑Tαtft(x))(11)
相当于所有弱分类器乘以分类器权重( α t = l n ( 1 − ϵ t / ϵ t ) \alpha_t=ln\sqrt{(1-\epsilon_t/\epsilon_t)} αt=ln(1−ϵt/ϵt))的求和,把输入 x x x丢进去,就可以得到 x x x的所属分类。
要证明的结论:随着 f t f_t ft中的 T T T增加, H ( x ) H(x) H(x)在training data上的错误率会慢慢变小。
先给出 H ( x ) H(x) H(x)在training data: x n x^n xn(有N笔数据)上的错误率:
(12) 1 N ∑ n δ ( H ( x n ) < > y ^ n ) \frac{1}{N}\sum_n\delta(H(x^n)<>\widehat y^n)\tag{12} N1n∑δ(H(xn)<>y n)(12)
把公式(11)中的右边用 g ( x ) = ∑ t = 1 T α t f t ( x ) g(x)=\sum_{t=1}^T\alpha _tf_t(x) g(x)=∑t=1Tαtft(x)代替,公式(12)变成:
(13) 1 N ∑ n δ ( y ^ n g ( x n ) < 0 ) \frac{1}{N}\sum_n\delta(\widehat y^ng(x^n)<0)\tag{13} N1n∑δ(y ng(xn)<0)(13)
由于是错误分类所以 y ^ n g ( x n ) < 0 \widehat y^ng(x^n)<0 y ng(xn)<0,公式(13)有一个upper bound:
(14) ≤ 1 N ∑ n e x p ( − y ^ n g ( x n ) ) ≤\frac{1}{N}\sum_nexp(-\widehat y^ng(x^n))\tag{14} ≤N1n∑exp(−y ng(xn))(14)
原理:
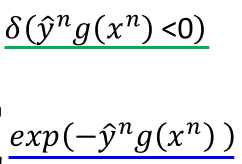
这里对应的函数图像为:
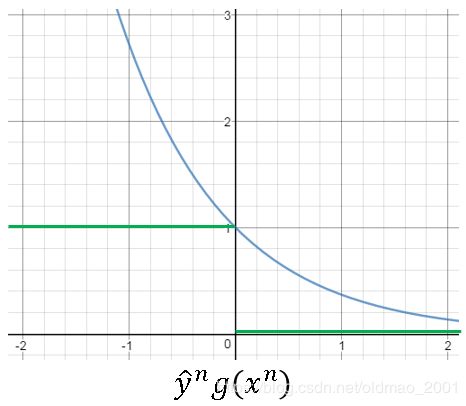
绿色对绿色,蓝色对蓝色。
现在的证明变成:upper bound会越来越小,算之前先看下 Z t Z_t Zt
Z t Z_t Zt:the summation of the weights of training data for training f t f_t ft,用公式表达为:
(15) Z T + 1 = ∑ n u T n + 1 Z_{T+1}=\sum_nu_T^n+1\tag{15} ZT+1=n∑uTn+1(15)
第一次迭代的权重为1: u 1 n = 1 u_1^n=1 u1n=1
第t+1次迭代的权重为: u t + 1 n = u t n × e x p ( − y ^ n f t ( x n ) α t ) u_{t+1}^n=u_t^n×exp(-\widehat y^nf_t(x^n)\alpha_t) ut+1n=utn×exp(−y nft(xn)αt),这个公式在AdaBoost算法那节的截图的红色框框里面有。
由 u 1 n u_1^n u1n和 u t + 1 n u_{t+1}^n ut+1n两个公式,可以推出来:
(16) u T + 1 n = ∏ t = 1 T e x p ( − y ^ n f t ( x n ) α t ) u_{T+1}^n=\prod _{t=1}^Texp(-\widehat y^nf_t(x^n)\alpha_t)\tag{16} uT+1n=t=1∏Texp(−y nft(xn)αt)(16)
将公式(16)带入(15)得:
(17) Z T + 1 = ∑ n ∏ t = 1 T e x p ( − y ^ n f t ( x n ) α t ) Z_{T+1}=\sum_n\prod _{t=1}^Texp(-\widehat y^nf_t(x^n)\alpha_t)\tag{17} ZT+1=n∑t=1∏Texp(−y nft(xn)αt)(17)
指数相乘相当于指数项相加,所以可以把公式(17)中的连乘号挪到指数项中变成求和,然后把括号中求和部分就是上面提的 g ( x ) g(x) g(x):
(18) Z T + 1 = ∑ n e x p ( − y ^ n ∑ t = 1 T f t ( x n ) α t ) = ∑ n e x p ( − y ^ n g ( x n ) ) Z_{T+1}=\sum _nexp\left(-\widehat y^n\sum _{t=1}^Tf_t(x^n)\alpha_t\right )=\sum_nexp(-\widehat y^ng(x^n))\tag{18} ZT+1=n∑exp(−y nt=1∑Tft(xn)αt)=n∑exp(−y ng(xn))(18)
观察公式(18),带入upper bound的公式(14)
公式(18)中括号中求和部分就是上面提的 g ( x ) g(x) g(x),变成:
(19) ≤ 1 N ∑ n e x p ( − y ^ n g ( x n ) ) = 1 N Z T + 1 ≤\frac{1}{N}\sum_nexp(-\widehat y^ng(x^n))=\frac{1}{N}Z_{T+1}\tag{19} ≤N1n∑exp(−y ng(xn))=N1ZT+1(19)
因此现在的证明目标变成公式(19)中的右边是越来越小。现在来分析一下 Z Z Z
Z 1 = N Z_1=N Z1=N初始化的时候所有权重都为1
Z t = Z t − 1 ϵ t e x p ( α t ) + Z t − 1 ( 1 − ϵ t ) e x p ( − α t ) Z_t=Z_{t-1}\epsilon_texp(\alpha_t)+Z_{t-1}(1-\epsilon_t)exp(-\alpha_t) Zt=Zt−1ϵtexp(αt)+Zt−1(1−ϵt)exp(−αt),其中 Z t − 1 ϵ t Z_{t-1}\epsilon_t Zt−1ϵt是 Z t − 1 Z_{t-1} Zt−1是错误分类的部分, Z t − 1 ( 1 − ϵ t ) Z_{t-1}(1-\epsilon_t) Zt−1(1−ϵt)是 Z t − 1 Z_{t-1} Zt−1是正确分类的部分。按AdaBoost算法中的截图红框中的公式,分类正确的乘以 e x p ( α t ) exp(\alpha_t) exp(αt),分类错误的乘以 e x p ( − α t ) exp(-\alpha_t) exp(−αt),接下来把 α t = l n ( 1 − ϵ t / ϵ t ) \alpha_t=ln\sqrt{(1-\epsilon_t/\epsilon_t)} αt=ln(1−ϵt/ϵt)带入 Z t Z_t Zt
(20) Z t = Z t − 1 ϵ t ( 1 − ϵ t / ϵ t ) + Z t − 1 ( 1 − ϵ t ) ϵ t / ( 1 − ϵ t ) = Z t − 1 × 2 ϵ t / ( 1 − ϵ t ) Z_t=Z_{t-1}\epsilon_t\sqrt{(1-\epsilon_t/\epsilon_t)}+Z_{t-1}(1-\epsilon_t)\sqrt{\epsilon_t/(1-\epsilon_t)}=Z_{t-1}×2\sqrt{\epsilon_t/(1-\epsilon_t)}\tag{20} Zt=Zt−1ϵt(1−ϵt/ϵt)+Zt−1(1−ϵt)ϵt/(1−ϵt)=Zt−1×2ϵt/(1−ϵt)(20)
由于 ϵ t \epsilon_t ϵt是错误率最大值为0.5,所以 2 ϵ t / ( 1 − ϵ t ) 2\sqrt{\epsilon_t/(1-\epsilon_t)} 2ϵt/(1−ϵt)最大是1,可以推断:
Z t < Z t − 1 Z_t<Z_{t-1} Zt<Zt−1
也就是 Z t Z_t Zt会越来越小:
(21) Z T + 1 = N ∏ t = 1 T 2 ϵ t / ( 1 − ϵ t ) Z_{T+1}=N\prod_{t=1}^T2\sqrt{\epsilon_t/(1-\epsilon_t)}\tag{21} ZT+1=Nt=1∏T2ϵt/(1−ϵt)(21)
将公式(21)带入上限公式把N消掉,上限可以表示为:
T r a i n i n g D a t a E r r o r R a t e ≤ ∏ t = 1 T 2 ϵ t / ( 1 − ϵ t ) < 1 Training Data Error Rate≤\prod_{t=1}^T2\sqrt{\epsilon_t/(1-\epsilon_t)}<1 TrainingDataErrorRate≤t=1∏T2ϵt/(1−ϵt)<1
AdaBoost结果分析
图中上面的线是testing set的结果,下面training set的结果。
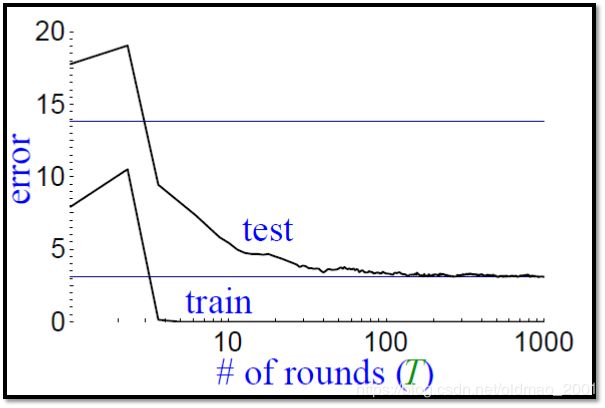
神奇的地方:Even though the training error(多个分类器组合后的结果) is 0, the testing error still decreases?为什么?
回顾上节的证明中拿到的终极分类器 H ( x ) H(x) H(x)
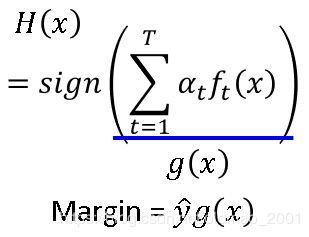
然后定义个Margin,意思是不但希望 y ^ g ( x ) \widehat yg(x) y g(x)的结果为正(分类正确),并且希望这个值越大越好(怎么听起来像SVM),如果观察margin变化的图就可以看到:
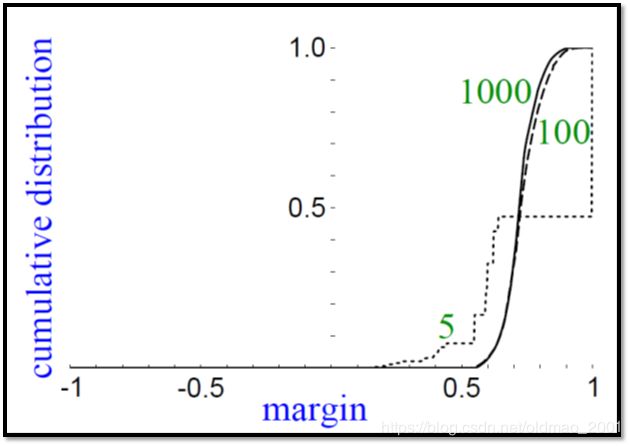
里面显示了5个,100个,1000个分类器组合后的margin变化,虽然迭代后错误率不在下降,但是margin不断变大,也就是 H ( x ) H(x) H(x)的鲁棒性越来越好,在testing上效果也就越来越好,
简单说明下margin为什么会不断增加,简单看看:
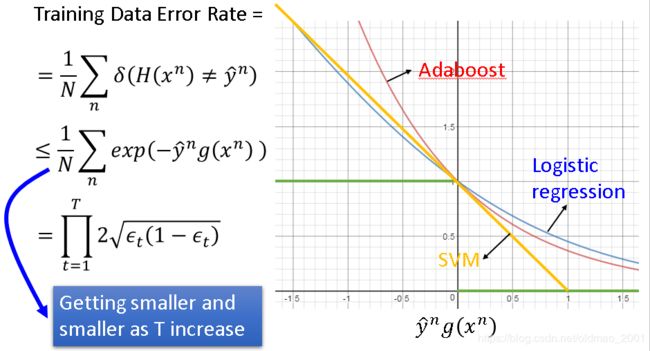
如果只是按绿色的线来看,只要 y ^ n g ( x n ) > 0 \widehat y^ng(x^n)>0 y ng(xn)>0错误率就为0了,没有什么改进空间。
反观红色的线,随着 y ^ n g ( x n ) \widehat y^ng(x^n) y ng(xn)增大错误率是慢慢减小的,当然逻辑斯蒂回归和SVM都有如此效果。
AdaBoost+决策树实例
Gradient Boosting
相当于boosting的一般形式,算法过程描述如下图:
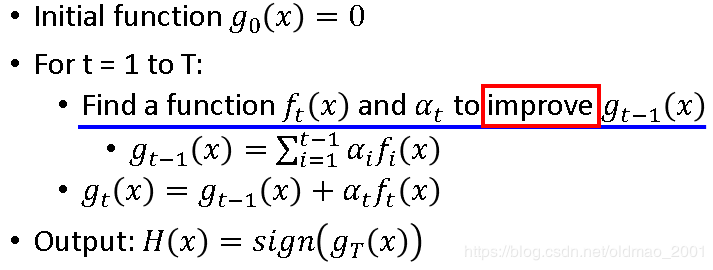
迭代T次,每次迭代都找一个弱分类器function: f t ( x ) f_t(x) ft(x)和它的权重 α t \alpha_t αt,两个东西会improve一个function: g t − 1 ( x ) g_{t-1}(x) gt−1(x),其公式见上图, g t − 1 ( x ) g_{t-1}(x) gt−1(x)和 f t ( x ) f_t(x) ft(x)是互补的,会使得 g t ( x ) g_{t}(x) gt(x)会变好。
g t ( x ) g_{t}(x) gt(x)怎么找到的?先设定它的learning target,就是cost函数
L ( g ) = ∑ n l ( y ^ n , g ( x n ) ) = ∑ n e x p ( y ^ n , g ( x n ) ) L(g)=\sum_nl(\widehat y^n,g(x^n))=\sum_nexp(\widehat y^n,g(x^n)) L(g)=n∑l(y n,g(xn))=n∑exp(y n,g(xn))
上面用指数函数作为衡量二者距离的标准是没问题的,因为在这个函数中,希望二者同号,且越大越好,就是可以最小化这个cost函数。下面用GD方法来解决这个问题:

这里比较抽象,思路大概这样,上面的红框是从GD列出来的式子,下面红框是从AdaBoost的算法得出来的式子,二者都是算 g t ( x ) g_t(x) gt(x),所以红框部分是要同向,才能使得迭代后越来越接近目标,绿色部分根据 L ( g ) L(g) L(g)的公式对g求偏导就这个绿箭头指向的结果。也就是想要下面两个式子同向
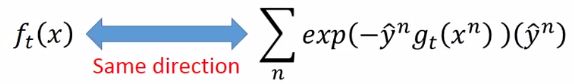
函数可以看做是vector,两个vector要同向,就是找到一个 f t ( x ) f_t(x) ft(x)使得两个连乘最大,so,把它们乘起来:
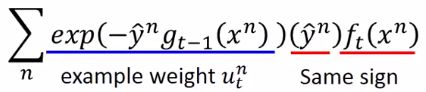
对于每一笔training data,都希望 y ^ n \widehat y^n y n和 f t ( x n ) f_t(x^n) ft(xn)同号,然后再乘上一个权重,这个权重刚好是之前在Adaboost算法中弄出来的,(具体位置在AdaBoost算法这节的截图中的红框下面一个公式)
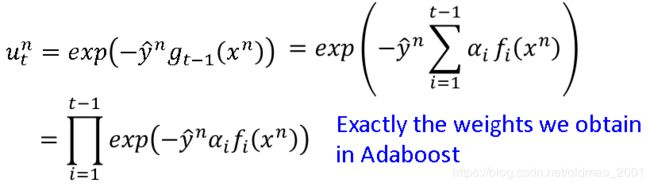
接下来讲的内容我也不是很理解,貌似是求出 f t ( x ) f_t(x) ft(x)之后, α t \alpha _t αt相当于learning rate
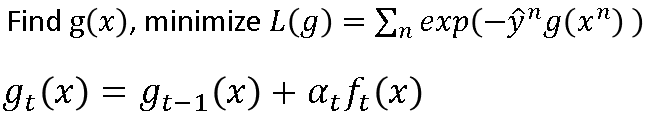
问题就变成找到 α t \alpha _t αt最小化 L ( g ) L(g) L(g),具体推导也没详细讲,就直接给了结论:
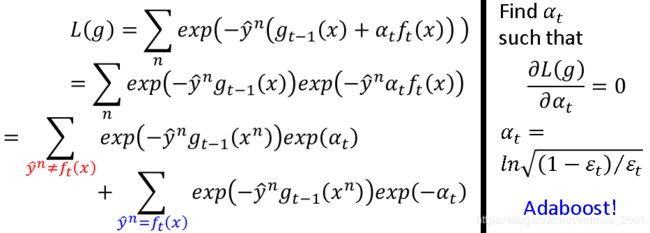
AdaBoost思想可以想象成为:Gradient是一个函数 f t ( x ) f_t(x) ft(x),learning rate是 α t \alpha _t αt,这样想了之后好处就是可以更换objective function,现在用的exp的目标函数,用GD的思想则可以换成别的目标函数,相当于自定义的AdaBoost。
Stacking
大概框架是这样: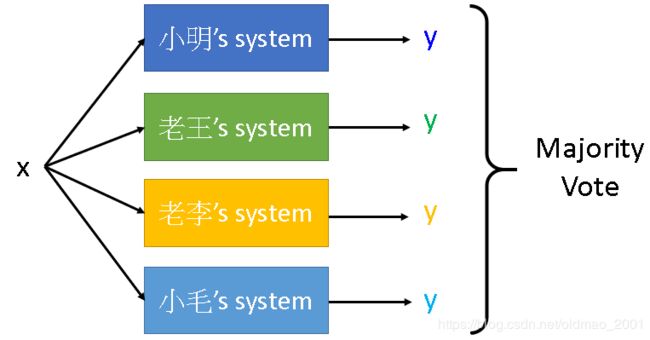
问题在于:小毛的系统可能很烂,输出都是随机的,因此在stacking的时候需要考虑权重,但考虑把小毛的系统权重设置太低小毛会伤心。把四个系统的输出y看做一个新feature,再输入到一个Final Classifier(因为前面已经处理过了,这里的classifier可以是简单的逻辑斯蒂回归等简单的分类器)

使用这个方法在划分数据集的时候要注意,一般方法都是一个training set,这里要吧training set分两部分,一部分用来训练四个系统,一个用来训练final classifier。分开原因很简单,如果不分开,大家都用同一个training set,小毛的系统作弊直接照抄training set的label(过拟合),Final Classifier由于使用的同一个training set,会觉得小毛的系统很强,最后造成在预测的时候会烂掉。使用不同的traini set,final classifier就能客观判断谁的系统很烂,然后给谁的系统很低的权重。