统计学习方法（5）集成学习（提升方法）：bagging和boosting

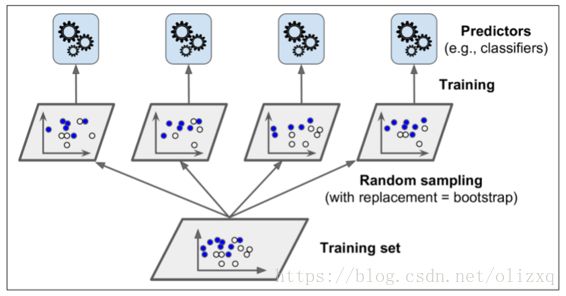
1、Bagging：

基于并行策略：基学习器之间不存在依赖关系，可同时生成。

基本思路：

• 利用自助采样法对训练集随机采样，重复进行 T 次;
• 基于每个采样集训练一个基学习器，并得到 T 个基学习器；
• 预测时，集体投票决策。

自助采样法：对 m 个样本的训练集，有放回的采样 m 次；
此时，样本在 m 次采样中始终没被采样的概率约为 0.368，即每次自助采样只能采样到全部样本的 63% 左右。

采样和训练过程:

特点：

• 训练每个基学习器时只使用一部分样本；
• 偏好不稳定的学习器作为基学习器；
• 每一个单独的分类器在原始训练集上都是高偏差，但是聚合降低了偏差和方差。

所谓不稳定的学习器，指的是对样本分布较为敏感的学习器。

为什么不稳定的学习器更适合作为基学习器？

• 不稳定的学习器容易受到样本分布的影响（偏差大），很好的引入了随机性；这有助于在集成学习（特别是采用 Bagging 策略）中提升模型的泛化能力。
• 为了更好的引入随机性，有时会随机选择一个特征子集中的最优分裂特征，而不是全局最优（随机森林）。

---

2、随机森林：

随机森林是bagging方法的典型应用，随机森林算法是以决策树算法为基础，通过bagging算法采样训练样本，再抽样特征，3者组合成的算法。对应scikit-learn中为RandomForestClassifier (RandomForestRegression)，它有着决策树(DecisionTreeClassifier)的所有参数，以及bagging(BaggingClassifier)的所有参数。

当处理高维(多特征)数据(例如: 图像)时，这种方法比较有用。同时对训练数据和特征进行抽样称为Random Patches，只针对特征抽样而不针对训练数据抽样是Random Subspaces。

随机的意义？
不管是对样本的随机采样，还是对特征的抽样，甚至对切分点的随机划分，都是为了引入偏差，使基分类器之间具有明显的差异，相互独立，提升模型的多样性，使模型不会受到局部样本的影响，从而减少方差，提升模型的泛化能力。

随机森林如何用于分类和回归？

• 分类
  随机森林采用投票的方式实现分类，对于训练好的随机森林模型，输入数据后，每棵树都会输出对应的分类，最终模型输出的分类结果是预测结果出现最多的分类（多数投票，硬投票）。
  如果基分类器支持输出每个分类的概率，则可以采用软投票的方式，对输入数据得到每个分类的预测概率，最终输出概率最大的分类。

• 回归
  随机森林的基分类器采用回归树，给定输入数据，每棵树都会输出对应的预测结果，最终的预测结果为每棵树预测输出的平均值。

---

3、Boosting：

基于串行策略：基学习器之间存在依赖关系，新的学习器需要根据上一个学习器生成。

基本思路：

• 先从初始训练集训练一个基学习器，初始训练集中各样本的权重是相同的；
• 根据上一个基学习器的表现，调整样本权重，使分类错误的样本得到更多的关注；
• 基于调整后的样本分布，训练下一个基学习器；
• 测试时，对各基学习器加权得到最终结果

特点：

• 每次学习都会使用全部训练样本

代表算法：

• AdaBoost 算法
• GBDT 算法

---

4、AdaBoost算法：

AdaBoost 算法还有另一个解释，即可以认为AdaBoost算法是模型为加法模型、损失函数为指数函数、学习算法为前向分步算法时的二类分类学习方法。

• AdaBoost 算法是前向分步算法的特例。
• 此时，基函数为基分类器，损失函数为指数函数L(y,f(x)) = exp(-y*f(x))

AdaBoost如何用于分类和回归？

• 分类
  AdaBoost算法串行训练生成一系列分类器，最终得到的模型如下：
  $$f(x)=sign(\sum _{k=1}^K{\alpha }_k{G}_k(x))$$
  给定输入数据$x$，每个分类器输出对应的预测结果（1，-1），预测结果乘以相应的权重${\alpha }_k$求和，对结果取sign可以获得输入数据的分类。

AdaBoost二元分类问题算法流程
输入为样本集$T=(x_1,y_1),(x_2,y_2),...(x_m,y_m)$，输出为$-1,+1$，弱分类器算法, 弱分类器迭代次数K。
输出为最终的强分类器f(x)
（1）初始化样本集权重为
$$D(1)=(w_{11},w_{12},...w_{1m});w_{1i}=\frac{1}{m};i=1,2...m$$
（2）对于$k=1,2，...K$:
\qquad a) 使用具有权重$D_k$的样本集来训练数据，得到弱分类器$G_k(x)$
\qquad b)计算$G_k(x)$的分类误差率
$$e_k=P(G_k(x_i)̸=y_i)=\sum _{i=1}^m{w}_{ki}I(G_k(x_i)̸=y_i)$$
\qquad c) 计算弱分类器的系数
$${\alpha }_k=\frac{1}{2}log\frac{1-e_k}{e_k}$$
\qquad d) 更新样本集的权重分布
$$w_{k+1,i}=\frac{w_{ki}}{Z_K}exp(-{\alpha }_k{y}_i{G}_k(x_i))i=1,2,...m$$
这里$Z_k$是规范化因子
$$Z_k=\sum _{i=1}^m{w}_{ki}exp(-{\alpha }_k{y}_i{G}_k(x_i))$$
（3）构建最终分类器为：
$$f(x)=sign(\sum _{k=1}^K{\alpha }_k{G}_k(x))$$
对于Adaboost多元分类算法，其实原理和二元分类类似，最主要区别在弱分类器的系数上。比如Adaboost SAMME算法，它的弱分类器的系数
$${\alpha }_k=\frac{1}{2}log\frac{1-e_k}{e_k}+log(R-1)$$
其中R为类别数。从上式可以看出，如果是二元分类，R=2，则上式和我们的二元分类算法中的弱分类器的系数一致。

• 回归
  回归算法利用每个样本相对于训练集上最大误差的相对误差来计算回归误差率，从而得到基学习器的权重，最终得到模型：
  $$f(x)=\sum _{k=1}^K(ln\frac{1}{{\alpha }_k})g(x)$$其中，$g(x)$是所有${\alpha }_k{G}_k(x),k=1,2,....K$的中位数。
  对于给定输入$x$，对所有基分类器输出加权求和得到回归结果。

AdaBoost回归问题的算法流程
输入为样本集$T=(x_1,y_1),(x_2,y_2),...,(x_m,y_m)$，弱学习器算法, 弱学习器迭代次数K。
输出为最终的强学习器$f(x)$
（1）初始化样本集权重为
$$D(1)=(w_{11},w_{12},...w_{1m});w_{1i}=\frac{1}{m};i=1,2...m$$
（2）对于$k=1,2,...,K$:
a) 使用具有权重$D_k$的样本集来训练数据，得到弱学习器$G_k(x)$
b) 计算训练集上的最大误差
$$E_k=max|y_i-G_k(x_i)|i=1,2...m$$
c) 计算每个样本的相对误差:
如果是线性误差，则$e_{k_i}=\frac{|y_i-G_k(x_i)|}{E_k}$；
如果是平方误差，则$e_{k_i}=\frac{(y_i-G_k(x_i){)}^2}{E_k^2}$；
如果是指数误差，则$e_{k_i}=1-exp(\frac{-|y_i-G_k(x_i)|}{E_k})$
d) 计算回归误差率
$$e_k=\sum _{i=1}^m{w}_{k_i}{e}_{k_i}$$
c) 计算弱学习器的系数
$${\alpha }_k=\frac{e_k}{1-e_k}$$
d) 更新样本集的权重分布为
$$w_{k+1,i}=\frac{w_{k_i}}{Z_k}{\alpha }_k^{1-e_{k_i}}$$
这里$Z_k$是规范化因子
$$Z_k=\sum _{i=1}^m{w}_{k_i}{\alpha }_k^{1-e_{k_i}}$$

3. 构建最终强学习器为：
   $$f(x)=\sum _{k=1}^K(ln\frac{1}{{\alpha }_k})g(x)$$
   其中，$g(x)$是所有${\alpha }_k{G}_k(x),k=1,2,....K$的中位数。

---

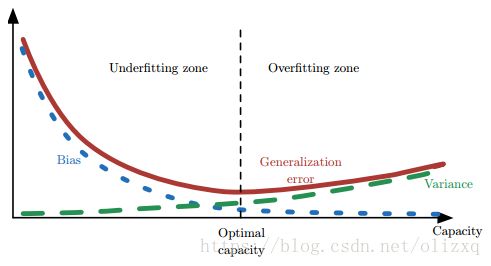
5、Boosting/Bagging 与 偏差/方差 的关系

• 简单来说，Boosting 能提升弱分类器性能的原因是降低了偏差；Bagging 则是降低了方差；

• Boosting 方法：

  • Boosting 的基本思路就是在不断减小模型的训练误差（拟合残差或者加大错类的权重），加强模型的学习能力，从而减小偏差；
  • 但 Boosting 不会显著降低方差，因为其训练过程中各基学习器是强相关的，缺少独立性。

• Bagging 方法：

  • 对 n 个独立不相关的模型预测结果取平均，方差是原来的 1/n；
  • 假设所有基分类器出错的概率是独立的，超过半数基分类器出错的概率会随着基分类器的数量增加而下降。

• 泛化误差、偏差、方差、过拟合、欠拟合、模型复杂度（模型容量）的关系图：
  

---

参考：
《统计学习方法》 李航
https://www.cnblogs.com/pinard/p/6133937.html