深度学习系列(六)：自编码网络的特征学习

在第三节我们已经介绍了
简单网络的自编码学习
知道了自编码学习其实就是学习到了输入数据的隐含特征，通过新的特征来表征原始数据，本节将介绍如何使用这些隐含特征进行模式分类；
还是以前面的三层自编码网络：

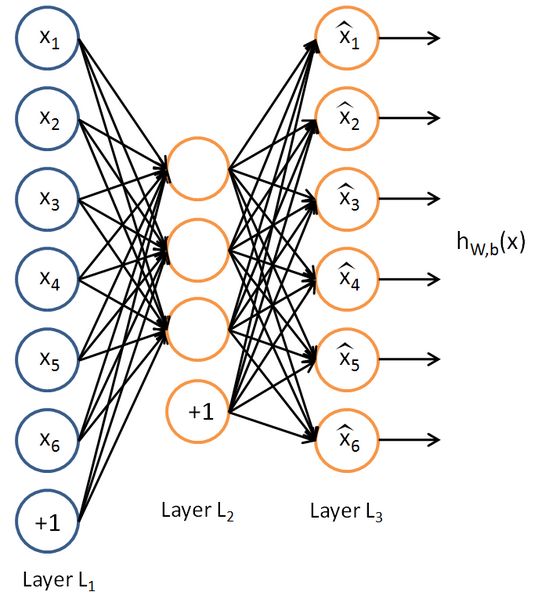
抽象一下如下：

其中学习到的权值系数W1与W1’是不一样的，我们把W1叫做编码权值，W1’叫做译码权值，原始数据在编码权值下的新数据Y就可以视为学习到了新维度下的数据，这在第三节也说过。那么如果我们用自编码学习并计算出到Y，再把Y用于分类，就可以构成神经网络的分类器了，网络深了就是深度网络的分类器了，当然后面接分类器可以是常用的分类器，比如SVM，贝叶斯，logistics，等等，也可以在接一个神经网络分类器。本实验为了比较我们在Y后面接SVM分类器看看，那么在上面一步完成后我们的分类器就变成下面这样子：

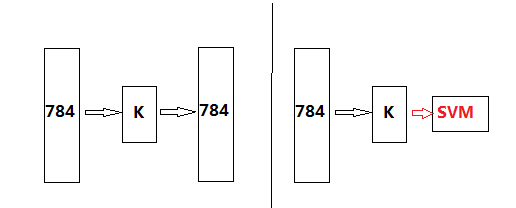
这里我们以手写体实验，所以输入固定了为784维。至于隐含层为多少是可以设计的k。

Ok理论分析到此，我们来看看上节介绍的工具箱如何实现吧
。
首先是三层自编码网络的实现，假设k=100吧，那么我们网络结构是不是[784,100,784]，像第三节做的那样，只不过第三节没有权值的稀疏性，而在这里我们要加入稀疏性了与一些去噪功能了。

Ok找到在工具箱DeepLearnToolbox\tests\test_example_SAE.m文件
把要说明的拿出来：

function test_example_SAE
load mnist_uint8;
choose_num_train = 10000;
choose_num_test= 200;
%初始化预处理
train_x = double(train_x(1:choose_num_train,:))/255;
test_x  = double(test_x(1:choose_num_test,:))/255;
train_y = double(train_y(1:choose_num_train,:));
test_y  = double(test_y(1:choose_num_test,:));

%%  ex1 train a 100 hidden unit SDAE and use it to initialize a FFNN
%  Setup and train a stacked denoising autoencoder (SDAE)
rand('state',0)
sae = saesetup([784 100]);%自编码网络的初始化，输出==输入，所以省略第三个784
sae.ae{1}.activation_function       = 'sigm';%将隐含层激活函数设置为sigm
sae.ae{1}.learningRate              = 1;%定义学习率
sae.ae{1}.inputZeroMaskedFraction   = 0.5;%定义0模板大小
opts.numepochs =   1;%重复迭代次数
opts.batchsize = 100;%数据块大小--每一块用于一次梯度下降算法
sae = saetrain(sae, train_x, opts);%训练
visualize(sae.ae{1}.W{1}(:,2:end)')%可视化编码矩阵的权值

对此在说明几点：
（1）自编码网络的初始化saesetup，打开看看

function sae = saesetup(size)
    for u = 2 : numel(size)
        sae.ae{u-1} = nnsetup([size(u-1) size(u) size(u-1)]);
    end
end

可以看到网络为[size(u-1) size(u) size(u-1)]，因为是自编码输出等于输入个数；

（2）关于自编码的nnsetup，在这个nnsetup里面，因为我们想适当的稀疏下权值，所以改变初始化的参数nn.nonSparsityPenalty，假设设置为0.05.

（3）关于另一个参数说明：sae.ae{1}.inputZeroMaskedFraction =0.5，这个参数是什么意思呢？就是以一定概率将输入值变成0，增加输入的鲁棒性，抗噪声能力。我们可以再nntrain里面看到代码：

  %Add noise to input (for use in denoising autoencoder)
        if(nn.inputZeroMaskedFraction ~= 0)
            batch_x = batch_x.*(rand(size(batch_x))>nn.inputZeroMaskedFraction);
        End

这就是当inputZeroMaskedFraction 不为0时需要执行的，看看执行了什么，是不是人为将一些输入改变成0了呀？更直观的解释为，比如一个输入来了，大小为784*1，假设里面有100个0，那么经过这么段程序后可能就变成了200个0了，防止过拟合作用，理解了吧，对于这种抗造性的网络修改操作，还有一篇相关论文专门介绍的可以看看http://www.cs.toronto.edu/~hinton/absps/dropout.pdf

最后就是可视化这个结果了，那么可视化的是编码权值矩阵，也就是W1。按照上面的设置我们先来看看可视化的结果吧（第三节我们也有可视化的介绍，在哪里效果可不怎么样）：
（注意需要设置的几个参数：要把nnsetup里面的nn.nonSparsityPenalty=0.05）

可以看到，编码矩阵的可视化结果，很明显的有一些手写体轮廓痕迹吧。把nn.nonSparsityPenalty调厉害点比如为0.2，结果为：

差了点吧，稀疏的越厉害，表示权值中需要归0或者很小的权值就越多，那么表示出来就是上面这个样子。这说明稀疏太狠了，就好像第四节中解释的那样子，本来一个向量至少需要3个基向量来表示才行，你非要稀疏到用一个基向量表示，结果能不差吗？

Ok，再来解释下这个可视化的结果到底是什么吧。把训练好的网络拿出来这样子的：

好了对于隐含层的100个单元的每一个单元，比如Y1,那么所有输入是不是有个权值到Y1，从Y(1,1)到Y(1,784),如上所示。那么再把这784向量变成28*28图像显示出来，就是输入相对于第一个隐含单元学到的特征权值，得到的值Y就是在这个隐含单元下的特征。这样还有其他99个隐含单元都显示出来就是上述见到的那个100个图了，每个图的大小为28*28。当然具体可视化的时候可能把数据归一化了等等处理了才显示出来的。

至此自编码特征学习、可视化到此了。784维数据经过编码就变成100维了，其实呢这个过程就是降维了，这就不经想起了这个过程非常像数据的PCA降维是不是，假设取784PCA一下变成100，你去研究发现他们出来的这100维结果其实很像，然而自编码更好，为什么？PCA毕竟给了个规则然后提取的特征，然而自编码呢？机器学习到的特征，这也就是为什么深度学习效果好，因为他的特征是自己学的，摆脱了传统意义上的手工设计的特征，相比之下，人再聪明，在其他条件一致的情况下，能比得过机器？而模式识别分类领域最重要的是什么？特征的选择，当特征的选择也可以用机器来做的时候，那么伟大的革新就即将诞生。

Ok扯远了，为了进一步比较深度学习学到的特征用于分类，以及与PCA的比较，待下回分享。