BP神经网络原理与应用-基于电影评分预测案例

BP神经网络简介

BP神经网络（Back Propagation Neutral Network）是1986年由Rumelhart和McCelland为首的科学家小组提出，是一种按误差逆传播算法训练的多层前馈网络，是目前应用最广泛的神经网络模型之一。BP神经网络使用最速下降法，通过反向传播不断调整网络的权值和阈值，是网络的误差平方和最小，从而实现模式识别等功能。

BP神经网络组成的结构包括有输入层、隐含层以及输出层，而每一层都有一定个数的神经元来接收、处理并输出数据。输入层主要负责接收输入参数，输入层神经元的数量取决于模型的输入特征数量，隐含层的层数以及每层所包含的神经元数量取决于对模型精度以及训练速度的要求，输出层神经元的数量取决于模型所要求的输出特征个数。

BP神经网络的训练在于对网络中各参数（神经元之间的权重以及阈值）的调整，使得整个模型误差最小。研究认为具有至少三层（单隐含层）的BP神经网络，考虑权重以及阈值的存在，可以无限逼近于任何有理函数。因此，不同于传统的多元线性回归方法，BP神经网络在解决非线性问题方面有着很好的优势，如异或（XOR）问题。

BP神经网络数学原理

BP神经网络结构图

上图显示了一个基本的BP神经网络构造图，其中包括5个输入节点（特征），5个隐含层节点，以及1个输出层节点

BP神经网络数学原理

• 本部分数学公式按照下部分案例进行讲解，设置输入层节点5个，隐含层节点5个，输出层节点1个
• 本案例中所有的激活函数，均采用 tan() 函数，没有采用不同的激活函数

1.参数定义

• 输入层输入值： xi(i为输入层节点个数) -> {x1,x2,x3,x4,x5}
• 隐含层净值： netHj(j表示隐含层节点个数) -> {netH1,netH2,netH3,netH4,netH5}
• 隐含层激活值： actHj -> {actH1,actH2,actH3,actH4,actH5}
• 输出层净值： netOz -> {netO1}
• 输出层激活值（网络预测值）： actOz -> {actO1}
• 输出层与隐含层间权重： wij -> {w11,w12,...,w54,w55}
• 隐含层与输出层间权重： vjz -> {v11,v21,v31,v41,v51}
• 隐含层偏置： bHj -> {bH1,bH2,bH3,bH4,bH5}
• 输出层偏置： bOz -> {bO1}
• 输出真实值： expz
• 学习速率： ρ

2.计算公式

(1) 向前传播过程

• 输入层到隐含层传播公式： netHj=∑5i=1xi∗wij；j=1,2,3,4,5
• 隐含层激活公式： actHj=f(netHj+bHj)；j=1,2,3,4,5
• 隐含层到输出层传播公式： netOz=∑5j=1actHj∗wij；z=1
• 输出层激活公式： actOj=f(netOz+bOz)；z=1

(2)反向传播调整误差过程

• 输出层神经元的梯度： δOz=(expz−actOz∗f(netOz)′)
• 隐含层神经元梯度： δHj=(∑1z=1(δOz∗vjz))∗f(netOz)
• 隐含层到输出层的权重调整量： Δvjz=ρ∗δOz∗actHj
• 输入层到隐含层权重调整量： Δwjz=ρ∗δHj∗xi
• 隐含层神经元偏置调整量： bHj=ρ∗δHj
• 输出层神经元偏置调整量： bOz=ρ∗δOz

BP神经网络应用案例-电影评分预测

1.数据描述

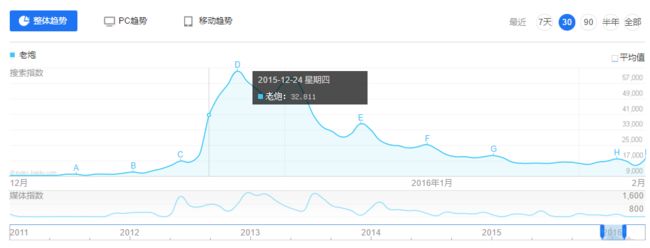
百度指数为本研究的数据收集提供了基础。通过在百度指数搜索器中输入电影名称，可以获得该关键词按时间范围上所有的次数，如图2所示，电影《老炮儿》于2015年12月24日上映，在该上映期间百度指数有明显的波动。

我们选择其中三个数据作为指标：
(1)电影上映前一天的百度指数 x1 ：在一定程度上反映了用户对于该电影的关注度，而这些关注度取决于商家对于电影的前期宣传
(2)电影上映当天的百度指数 x2 ：在一定程度上反映了电影上映初期用户对电影的喜欢程度
(3)电影上映后一天百度指数（相比上映当天）变化量百分比 x3 ：在一定程度上反映了用户对于电影的真实评价对搜索量的影响

此外，我们选择是否为国产电影 x4 ，以及是否为3D电影 x5 作为控制变量，共5个参数。收集2015年上映的25个电影作为训练样本（由于电影样本较少，因此采用重复训练的方式来扩大样本量），收集2014年上映的8个电影作为测试集。

2.第一次训练

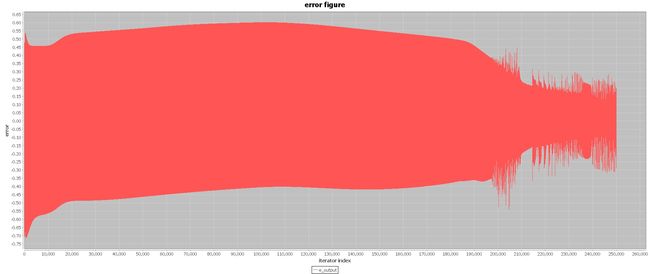
为了减少不同量纲的指标对网络的影响，在训练之前首先用excel将所有参数做归一化处理。采用重复训练的方式来进行第一次训练，学习速率为0.8，重复次数为10000次（共25个样本重复训练10000次，总共训练250000次）。训练结果如下：

训练在初期波动较大，在第210000次训练左右时，网络误差开始逐渐收敛，收敛的范围为±0.3之间。由于第一次训练我们采取快速的训练方式，网络中学习速率选择为0.8，防止陷入局部最优值，当网络开始收敛时，我们准备采用0.4较慢的学习速率寻找最优值，防止网络波动过大。

3.第二次训练

第二次训练过程，我们将学习速率调整到0.4，尝试得到全局最优解，网络中的权值以及阈值使用第一次训练结果进行初始化，重复训练次数2000次（共50000次训练），得到第二次训练结果如下：

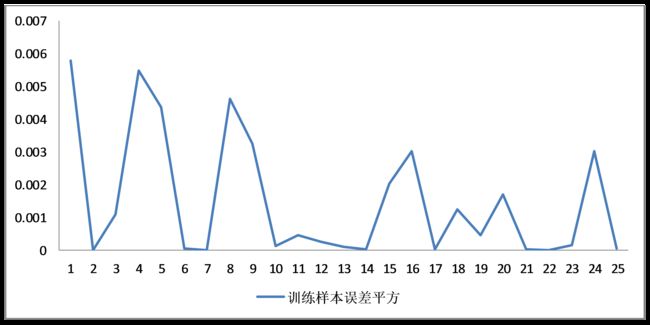
更小的学习速率的学习使得网络误差进一步收敛，误差范围为±0.075之间，相对于第一次训练，本次训练结果具有更好的收敛性，神经网络训练结束。

4.结果分析

网络训练最终结果（输入层与隐含层间权重）

输入层\隐含层	1	2	3	4	5
1	-12.2086	-12.8165	-4.07724	-4.4004	1.194808
2	-3.72075	-3.89653	-14.084	3.677251	1.773899
3	-20.3801	25.50715	-20.6775	-2.87621	-4.95111
4	15.73305	-9.14165	-11.8204	0.413969	-2.92611
5	-28.9022	26.19699	-0.85407	0.005734	6.469848

---

网络训练最终结果（隐含层与输出层间权重）

输出层\隐含层	1	2	3	4	5
1	5.903438	-11.6467	-10.4308	11.25273	8.904731

---

网络训练最终结果

偏置位置	1	2	3	4	5
隐含层	1.903043	-9.63593	6.906526	0.590284	3.239882
输出层	-7.43919	null	null	null	null

5.模型检验

使用训练好的参数初始化网络，对测试样本（2014年上映的8个电影）进行一次检验，得到训练结果图如下：

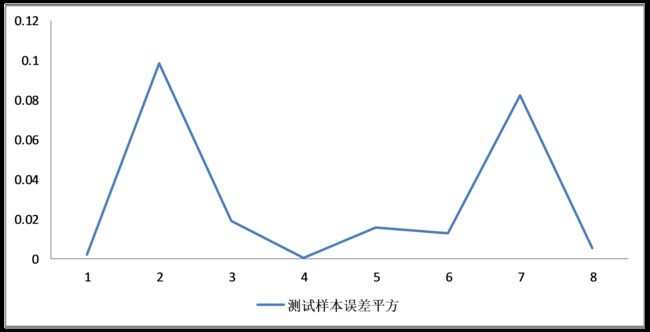
测试样本的误差在 {0.150 −0.3} 之间，误差平方小于0.1，模型的泛化能力得到了一定的验证，但是测试误差与训练误差有一些差距。

6.模型预测

尽管测试误差相比训练误差较大，但是从训练与测试的结果来看，我们认为在一定程度上用拥有预测能力，因此我们准备使用该网络对2016年上映的电影进行评分预测。研究选取的待预测样本为2016年4月8日上映的《伦敦陷落》，其特征值为 {32342，100893，126589，0，1} ，带入网络的参数为 {0.061266，0.06547，0.254686，0，1} ，输出结果为0.78，通过逆归一化，得出评分值为 。查询豆瓣现在对该电影的评分为6.30分。因此使用本研究模型，我们认为该电影评分未来可能有所增加。

关键部分JAVA源码

1.向前演算部分

public static void cal_forward(List input_array,List output_array){

        List hidden_active = new ArrayList();//隐层输出值
        //初始化
        for (int i=0;i0.0);
        }

        //输入层到隐层的向前推算
        for(int j=0;j//根据隐含层神经元个数限定次数
            for (int i=0;i//计算每一个隐含神经元权重输入值
                double x = input_array.get(i)*weight_input_hidden.get(i*hidden_number+j);
                hidden_active.set(j, hidden_active.get(j)+x);
            }
        }
        //计算隐层的激活输出值
        for(int i=0;iset(i, activefunction.cal_sigmoid(1,hidden_active.get(i)+bias_hidden.get(i))); 
        }

        List output_active = new ArrayList();//输出层输出值
        //初始化
        for (int i=0;i0.0);
        }
        //隐层到输出层的向前推算
        for(int j=0;jfor(int i=0;idouble x = hidden_active.get(i)*weight_hidden_output.get(i*output_number+j);
                output_active.set(j, output_active.get(j)+x);
            }
        }
        //计算输出层的激活输出值
            for(int i=0;iset(i, activefunction.cal_sigmoid(1,output_active.get(i)+bias_output.get(i))); 
            }

        //计算残差
            List e_output = new ArrayList();
            for(int i=0;iget(i)-output_active.get(i));
            }
            DecimalFormat df = new DecimalFormat("0.000"); 
            Label label_1  =   new  Label(0,index,index+""); 
            Label label_2  =   new  Label(1,index,e_output.get(0).toString()); 

            try {
                writesheet.addCell(label_1);
                writesheet.addCell(label_2);
            } catch (RowsExceededException e) {
                // TODO Auto-generated catch block
                e.printStackTrace();
            } catch (WriteException e) {
                // TODO Auto-generated catch block
                e.printStackTrace();
            }
            index = index+1;
            System.out.println(index);
            System.out.println(df.format(e_output.get(0)));
            xyseries_pingfang.add(index,(e_output.get(0))*(e_output.get(0)));
            xyseries_expectation.add(index,output_array.get(0)); 
            xyseries_actual.add(index,hidden_active.get(0));

2.反向传播调整权重

List output_gradient = new ArrayList();     
        for(int i=0;iget(i)*output_active.get(i)*(1-output_active.get(i)));
        }

        //计算隐层——————输出层权重调整
        List delta_hidden_output = new ArrayList();
        for(int i=0;ifor(int j=0;jget(j)*hidden_active.get(i));
            }
        }
        //计算输入层——————隐层权重调整 
        List delta_input_hidden = new ArrayList();
        List hidden_gradient = new ArrayList(); //
            for(int i=0;ifor(int j=0;j//计算隐层残差
                    double e_oper = 0.0;
                    for(int x=0;xget(x)*weight_hidden_output.get(j*output_number+x);
                    }
                    hidden_gradient.add(e_oper*hidden_active.get(j)*(1-hidden_active.get(j)));
                    delta_input_hidden.add(learning_speed*e_oper*hidden_active.get(j)*(1-hidden_active.get(j))*input_array.get(i)); 
                }
            }


        //调整参数
        //调整最外层权重
        for (int i=0; iset(i,weight_hidden_output.get(i)+delta_hidden_output.get(i));
        }
        //调整中间层权重   
        for (int i=0; iset(i,weight_input_hidden.get(i)+delta_input_hidden.get(i));
        }   
        //调整偏置      
        for (int i=0; iset(i, bias_output.get(i)+learning_speed*output_gradient.get(i));
        }
        for (int i=0; iset(i, bias_hidden.get(i)+learning_speed*hidden_gradient.get(i));
        }

参考文献

• [1] 周才庶. 电影票房与网络评分的关联性分析——以 2010 年票房过亿元的国产影片为例 [J]. 当代电影, 2011, 3): 109-13.
• [2] 李松, 刘力军, 翟曼. 改进粒子群算法优化 BP 神经网络的短时交通流预测 [J]. 系统工程理论实践, 2012, 32(9): 2045-9.
• [3] 熊熊, 马佳, 赵文杰, et al. 供应链金融模式下的信用风险评价 [J]. 南开管理评论, 2009, 12(4): 92-8.
• [4] 许兴军, 颜钢锋. 基于 BP 神经网络的股价趋势分析 [J]. 浙江金融, 2011, 11): 57-9.
• [5] 赵成, 柏岫, 毛春梅. 基于 ARIMA 和 BP 神经网络组合模型的我国碳排放强度预测 [J]. ResourceS and Environment in the Yangtze BaSin, 2012, 21(6):
• [6] 孙海峰, 甘明鑫, 刘鑫, et al. 国外电影推荐系统网站研究与评述 [J]. 计算机应用, 2013, 33(A02): 119-24.
• [7] 刘锋, 叶强, 李一军. 媒体关注与投资者关注对股票收益的交互作用: 基于中国金融股的实证研究 [J]. 管理科学学报, 2014, 17(1): 72-85.