DeepWalk 论文笔记

DeepWalk 论文笔记

针对论文[1]的阅读撰写阅读笔记。DeepWalk的代码实现

概述

这篇论文主要提出了在一个网络中，学习节点隐表达的方法——DeepWalk，这个方法在一个连续向量空间中对节点的社会关系进行编码，是语言模型和无监督学习从单词序列到图上的一个扩展。该方法将截断游走的序列当成句子进行学习。该方法具有可扩展，可并行化的特点，可以用来做网络分类和异常点检测。

贡献

论文贡献有三点：
1. 将深度学习应用到图分析中，构建鲁棒性的表示，其结果可应用于统计模型中
2. 将表示结果应用于一些社会网络的多标签分类任务中，与对比算法比较，大部分的 F1 值提高5-10%，有些情况下，在给定少于60%训练集的情况下，比其他对比方法要好
3. 论文通过构建互联网规模（例如YouTube）的并行化实现的表示，论证了方法的可扩展性，同时描述了构建流式版本的方法实现

问题描述

给定一个图 G=(V,E) ，以及部分标注的社会网络 GL=(V,E,X,Y) ，其中， X∈R|V|×S 是节点属性， S 是每个属性向量的特征空间的大小， Y∈R|V|×|y| 是节点的标签。论文的工作就是独立于标签 Y 的值，学习出 XE∈R|V|×d 的表示， d 是一个极小的隐空间维度。学习出来的社会化表示具有以下特点：

• 自适应性，真实的社会网络是不断变化的，新的社会化关系进来之后，应该不需要再重新执行一次学习过程
• 社区感知性，学出来的隐空间应该能够包含网络中同质节点或相似节点距离近的信息
• 低维度
• 连续性

---

论文选取的是随机游走序列，作为DeepWalk的输入。原因有：

• 随机游走能够包含网络的局部结构
• 使用随机游走可以很方便地并行化
• 当网络结构具有微小的变化时，可以针对变化的部分生成新的随机游走，更新学习模型，提高了学习效率
• 如果一个网络的节点服从幂律分布，那么节点在随机游走序列中的出现次数也应该服从幂律分布，论文通过实证发现自然语言处理中单词的出现频率也服从幂律分布。可以很自然地将自然语言处理的相关方法直接用于构建社区结构模型中。

---

针对一个自然语言处理问题，给定一个单词序列 Wn1=(w0,w1,...,wn) ，我们要用前 n−1 个单词来预测第n个单词，也就是最大化 Pr(wn|w0,w1,...,wn−1) 的问题。针对社会网络上的随机游走序列，我们自然会想到，要用前 n−1 个节点来预测第 n 个节点的出现 Pr(vn|v0,v1,...,vn−1) 。但是论文的目的是要学习一个隐表示，所以引入了一个映射函数 Φ:v∈V↦R|V|×d 。于是，问题变成估计 Pr(vn|Φ(v0),Φ(v1),...,Φ(vn−1)) 的问题。但是如果随机游走的长度变大，会降低该条件概率估计的效率。自然语言处理领域中，针对这个问题给出了几个解决方案：

• 把根据上下文预测一个单词的问题，变为根据一个单词预测上下文的问题
• 在一个给定单词的左边和右边都会出现上下文内容
• 去除单词出现的顺序约束

---

于是问题变成了最优化如下式子

minimizeΦ−logPr({vi−w,...,vi+w}∖vi|Φ(vi))

---

方法

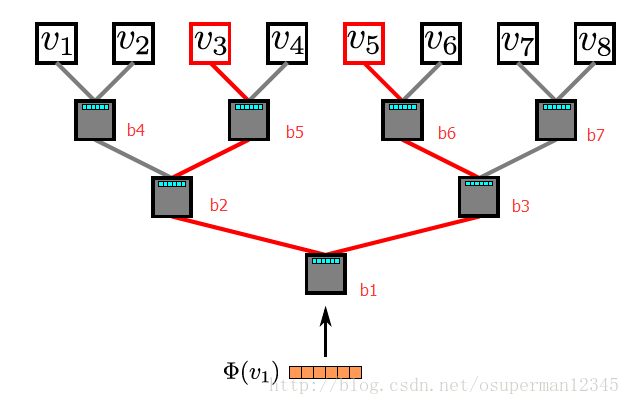
算法包含两个主要部分：一个随机游走生成器和一个更新过程。随机游走生成器随机均匀地选取网络节点，并生成固定长度的随机游走序列，每个节点生成长度为 t 的 γ 个随机游走序列，本文并没有使用重启的随机游走方法。为了加快算法的收敛，本文对图中所有的节点遍历一遍之后，再重新遍历所有节点，论文使用SkipGram算法来更新节点表示。SkipGram首先将每个节点 vi 与其表示一一映射，并有假设： Pr({vi−w,...,vi+w}∖vi|Φ(vi))=∏i+wj=i−w,j≠iPr(vj|Φ(vi)) ，通过最大化这个概率，来更新 Φ 的值。因为使用逻辑回归的方法，太耗时了，本文使用分层softmax的方法来训练。即将每个节点分配到二分类树的叶子节点上，本文使用哈夫曼编码对节点进行编码，将出现频繁的节点的路径设置较短。假设从根节点到一个节点 uk 的路径是一个树节点的序列 (b0,b1,...,b[log|V|]) ， b0 是根节点， b[log|V|] 表示节点 uk ，于是有 Pr(uk|Φ(vj))=∏[log|V|]l=1Pr(bl|Φ(vj)) ，其中， Pr(bl|Φ(vj))=1/(1+e−Φ(vj)∗Ψ(bl)) ， Ψ(bl) 是树上节点 bl 的父亲节点的隐表示。例如，在下图中，从根节点到 v3 节点的路径应为 b1,b2,b5,v3 将这些节点对应的概率累积算出来。

Pr(v3|Φ(v1))=1/((1+e−Φ(v1)∗Ψ(b1))(1+e−Φ(v1)∗Ψ(b2))(1+e−Φ(v1)∗Ψ(b5)))

这样算法复杂度就从 O(|V|) 降到了 O(log|V|) 。论文使用随机梯度下降的方法来优化参数，学习率在训练初始设置为2.5%，随着训练出节点的个数的增多，线性降低。

---

并行化

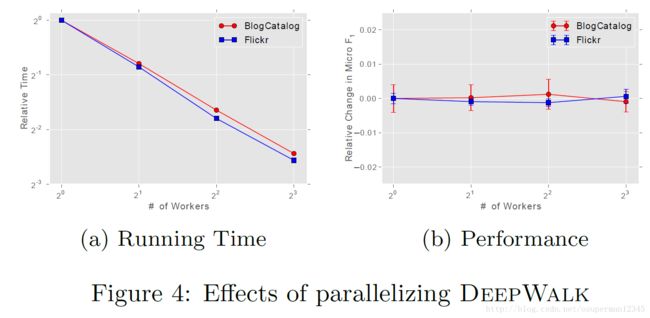
由于节的度服从长尾分布，因此针对 Φ 的更新的影响，会很稀疏。于是论文可以使用异步随机梯度下降的方法来更新 Φ 值。下图给出了DeepWalk的可扩展性的实验结果。

---

流式版本

这里，从图中获得一些随机序列，就直接应用到图的训练中。做了一些调整，将学习率 α 值设置的很低。另外，如果网络中的节点个数 V 是已知的，或者能够大致估计出来，那么我们还可以使用哈夫曼树对节点进行编码，否则就不能使用。

---

非随机游走

如果网络图是由相互交互的代理间的元素序列构成，例如用户在一个网站上的页面访问。那么我们可以直接使用这个序列作为输入，而不用使用随机游走来生成。一般这种网络，不仅包含结构信息，而且包含语义信息。

---

实验部分

实验部分就是各种说论文提出的算法有多么好了，对比的算法有，SpectralClustering，Modularity，EdgeCluster，wvRN，Majority。数据集有BlogCatalog，Flickr，YouTube。然后又做了参数敏感性分析，生成的隐表示的维度 d 的大小，不敏感。随机游走的个数越大越好，一般到了 25 以后算法提高的效果会比较低了，对学习率不是很敏感。

---

[1]: Perozzi B, Al-Rfou R, Skiena S. Deepwalk: Online learning of social representations[C]//Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining. ACM, 2014: 701-710.