CSDN机器学习笔记二 决策树、随机森林

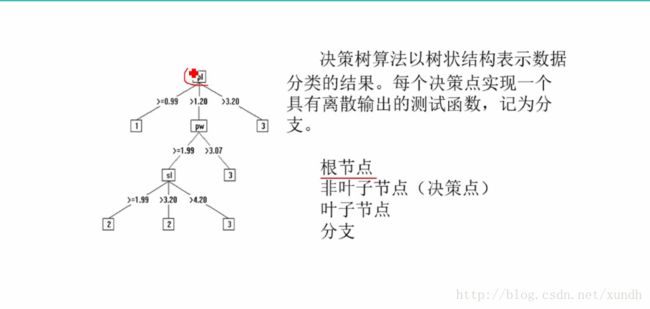
一、决策树

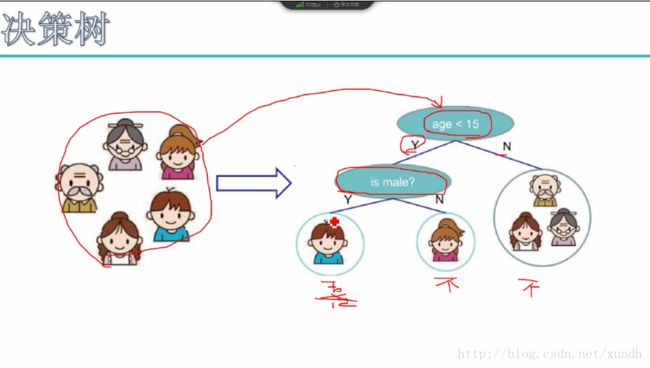
1..示例

要决策一个人喜不喜欢电子游戏。 

数据丢进去，数据通过节点一步步走，最终会到一个叶子节点，没有一个数据是在中间的。

1.训练阶段 
从给定的训练数据集DB，构造出一棵决策树

class=DecisionTree(DB)

• 1

• 1

2.分类阶段 
从根开始，按照决策树的分类属性逐层往下划分，直到叶节点，获得概念（决策、分类）结果。

y=DecisionTree(x)

• 1

• 1

另一个例子： 
明天有一个约会对象，要不要去见呢？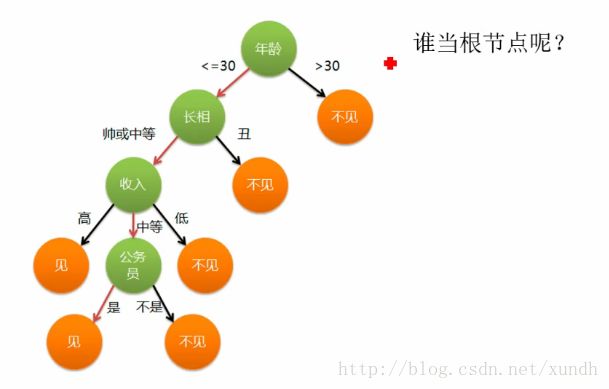 
 
年龄作用最大， 
长相其次，是按什么来决定 
哪些特征当根节点呢？当根节点，

2.决策树-熵

表示物体内部的混乱程度。

如：两个集合 
A：[1,2,3,4,2,1,3,5] 
B：[1,1,1,1,2,2,1] 
对于两个集合，它们的熵值A>B，因为A比较混乱。

越接近0，熵值越大。 
熵和Gini系数都是计算稳定系数。

计算熵的示例：

一批数据，明天去不去打球： 

首先选根节点， 
构造树的基本想法是随着树深度的增加，节点的熵迅速地降低。熵降低的速度越快越好，这样我们有望得到一棵高度最矮的决策树。 
在没有给定任何天气信息时，根据历史数据，我们只知道新的一天打球的概率是9/14，不打的概率是5/14。此时的熵为0.940：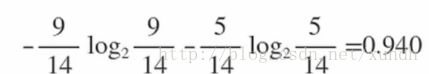 

属性有4个：outlook，temperature，humidity，windy。我们首先要决定哪个属性作为根节点。 
对每项指标分别统计：在不同的取值下打球和不打球的次数。

outlook=sunny时，2/5的概率打球，3/5的概率不打球，entropy=0.971 
outlook=overcast时,entropy=0 
outlook=rainy时,entropy=0.971

而根据历史编译数据，outlook取值为sunny，overcast，rainy的概率分别是5/14，4/14，5/14，所以当已知变量outlook的值时，信息熵为:5/14*0.971+4/14*0+5/14*0.971=0.693 
这样的话系统熵就从0.940下降到了0.693，信息增溢gain(outlook)为0.940-0.693=0.247 
同样可以计算出gain(temperature)=0.029,gain(humidity)=0.152,gain(windy)=0.048。 
gain(outlook)最大（即outlook在第一步使系统的信息熵下降得最快），所以决策树的根节点就取outlook。

然后同样的计算第二个节点。

如果加一个ID数据列，作为根节点的话。计算的熵值为0。其特征是属性非常多，每个分类的数据非常少。这样的数据我们最终希望把它剔除。

ID3：信息增益（很少使用） 
C4.5：信息增益率 
CART：Gini系数 
Gini系数和熵不要同时使用。

评价函数：建立完决策树，要评介它好不好。 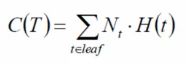 希望它越小越好，类似损失函数了。 
t是叶子节点，N_t代表一共的样本树。

对于连续值怎么处理（先要离散化）

选取（连续值的）哪个分界点？ 
贪婪算法

排序 
60

若进行“二分”，则可能有9个分界点。

例子： 
60 70 75,85 90 95 100 120 125 220

60 70 75 85 90 95,100 120 125 220 
分割成TaxIn<=97.5和Taxln>97.5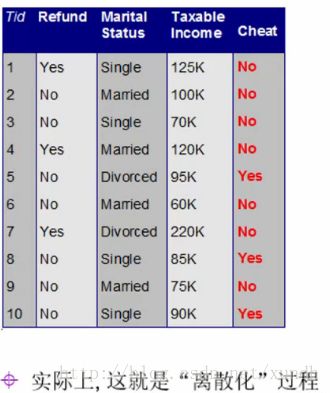 

 
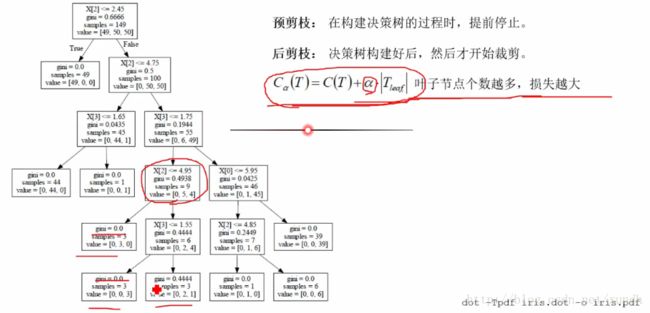
- 预剪树：数据太大了，在构建决策树的过程时，提前停止。 
- 后剪树：决策树构建好后，然后才开始裁剪。实际用的少。

C_α(T)=C(T)+α*|T_leaf| 
α就是个系数。 
叶子节点个数越多，损失越大。

二 、随机森林

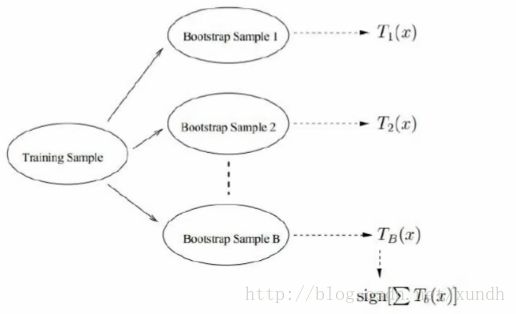
Bootstraping：有放回采样 
Bagging：有放回采样n个样本一共建立分类器

Forest：决策树是很多的，每个都要训练出来。 
Rand：随机，如现在有10个数据，这10个数据当中，有些在数据采集中出现了一些问题，如9号数据是错误数据，这些数据会使决策树看起来比较奇怪。 
随机森林进行了这样的假设：

• 第一重随机性，选择数据的时候随机选择其中6个，有放回的数据采样。每个树都是随机取了其中6个。不一定每棵树都会取到那个错误的数据。
• 第二重随机性，数据是由特征组成的，如一个数据有6个特征。每一个棵都随机从其中选4个特征。每个树评估标准、数据都是不一样的。 
  这样每个树就有了差异性，这样才能让结果更准。

三、sklearn

1. splitter best or random 随机选择
2. max_features 最多选多少个特征 特征小于50的时候一般使用所有的
3. mx_depth，
4. min_samples_split 对于某个叶子节点来说，指定小于10时不再划分
5. min_samples_leaf
6. min_weight_fraction_leaf 了样本权重
7. min_weight_fraction_leaf
8. max_leaf_nodes
9. class_weight 样本各类别的权重
10. min_impurity_split 这个值限制了决策树的增长