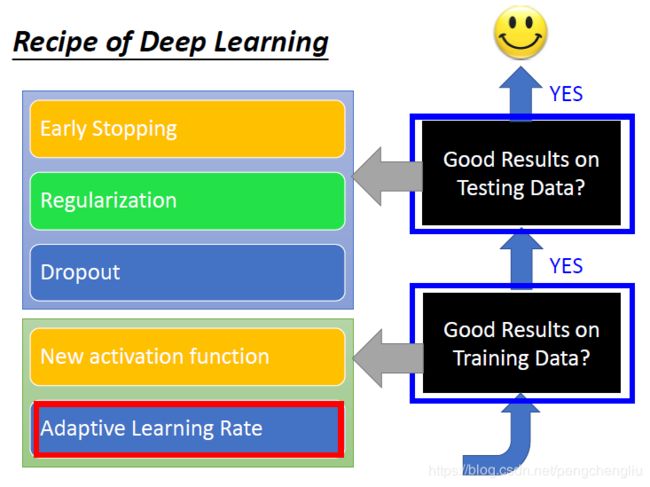
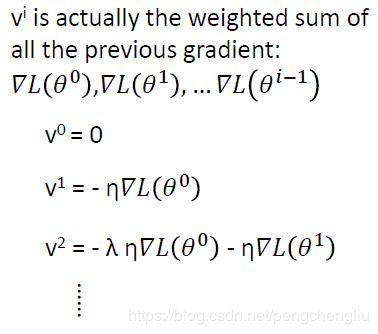神经网络的优化（2）----优化器、自适应学习率：Adagrad、RMSProp、Momentum、Adam

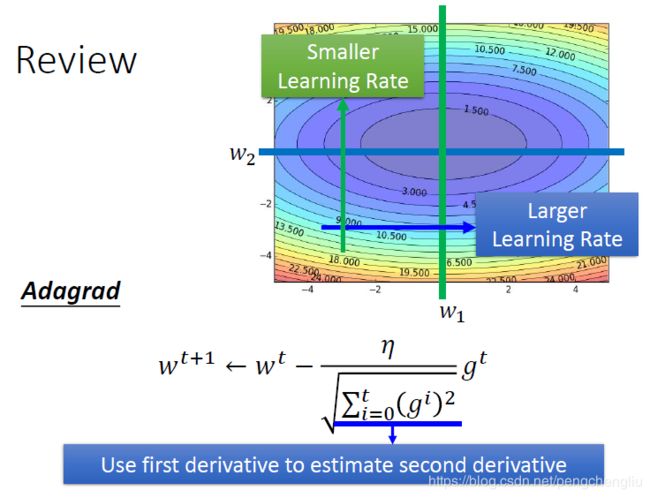
一、Adagrad        //这个优化器，带有自适应的学习率                                                                点击此处返回总目录 二、RMSProp      //Adagrad的进阶版，带有更好的自适应学习率 三、Momentum    //动量。 四、Adam            //RMSProp+Momentum。           下面开始讲，自适应学习率。                                     一、Adagrad 自适应的学习率，我们之前讲过。我们之前有讲过Adagrad。遗忘了可以回去看看。                                  但是实际上呢，我们面对的问题是有可能会比Adagrad可以处理的问题更加复杂的。也就是说，我们之前在做Linear Regression的时候呢，我们看到的Loss function是凸的。但是呢，我们在做deep learning的时候，loss function可以是任何形状。比如，它可以是下面这种怪异的月球的形状。当今天你的error surface是这个形状的时候，你会遇到的问题是，即使是同一个方向上，你的learning rate也必须能够快速地变动。对于convex的function，这个方向很平坦就一直很平坦，这个方向很陡峭，就一直很陡峭。但是，如果今天是更复杂的问题的时候，你考虑w1改变的这个方向，在某个区域它很平坦，所以它需要比较小的learning rate；但是到了另外一个区域，它又突然变得很陡峭，这时候需要比较大的learning rate。所以，要真正要处理deep learning的问题，用adagrad可能是不够的。你需要更动态地调整learning rate的方法。                               二、RMSProp 所以，这里有一个Adagrad的进阶版，叫RMSProp。RMSProp我觉得是一个蛮神奇的方法，你好像找不到他的paper，这个是在hitton的慕课里面提出来的。他在他的线上课程里面提出一个方法。大家引用的时候，要引用线上课程的youtoub链接。 这招还真的有用，RMSProp是这样做的。 我们用固定的learning rate eta除以一个值sigma，这个sigma是什么呢？在第一个时间点，sigma就是第一次算出来的gradient g0。在第二个时间点，算出来新的gradient g1，这个时候，sigma1就是原来的sigma的平方乘上alpha，再加上新的gradient的值g1的平方乘上(1-alpha),最后开根号。而这个alpha的值呢，是可以自由去调的。在下个时间点，也是这么算。 跟原来的adagrad不一样的地方是，原来的adagrad在分母放的值是g0,g1,g2的均方根。但是在RMSProp中，虽然也是包含g0,g1,g2的平方，但是可以给它乘上weight alpha或者是1-alpha，可以手动调整alpha的值（alpha的值可以手动设置）。当alpha的值设的小一点时，1-alpha比较大，那意思就是说你倾向于相信新的gradient所告诉你的这个error surface的平滑或陡峭的程度，而比较无视旧的gradient所给你的information。 所以当做RMSProp的时候，一样是在算gradient的均方根。但是你可以给现在的gradient比较大的weight，给过去的weight比较小的weight。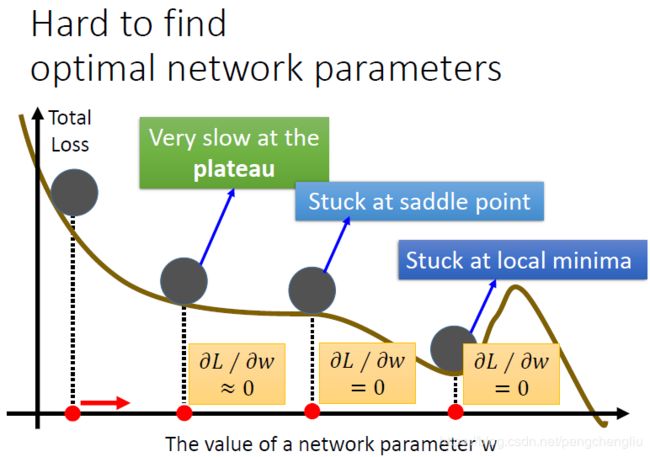                                     三、Momentum   好，那除了learning rate的时候，我们知道在做deep learning的时候，大家都会说我们回卡在local minimum的地方。我们之前说，不见得会卡在local minimum ,还有可能卡在saddle point，甚至卡在plateau的地方。大家听到这个问题都会非常的担心，说，做deep learning是非常困难的，因为随便做一下就有一大堆的问题。其实，lecun(没听清楚，应该是他)在07年的时候，就有一个蛮特别的说法，他说，你不用太担心local minimum的问题。他说，其实error surface上没有太多local minimum，所以不同太担心。为什么呢？他说，你要是一个local minimum，必须每一个dimension都是山谷的谷底，假设山谷谷底出现的几率是p，因为我们的网络有非常多的参数，假设有1000个参数，每个参数都是山谷的谷底，这个概率是p^1000。网络越大，参数越多，出现的记录就越低。所以，local minimum在一个很大的网络里面，其实没有想象的那么多。很大的网络其实搞不好是很平滑的。所以当走到你觉得是local minimum卡住的时候，他8成就是global minimum，或者很接近global minimum。这个想法给大家参考，如果有特别的想法，可以再交流。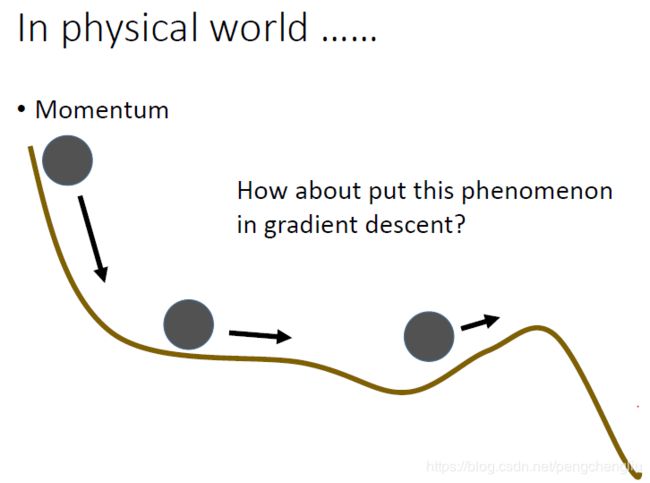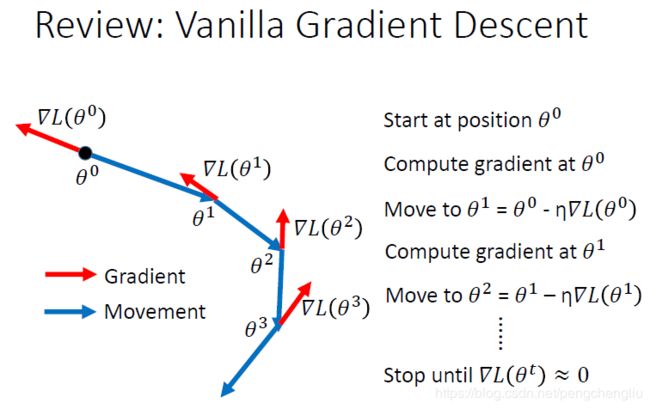                                        有一个方法可以处理local minima、saddle point 还有plateau的问题。这个想法呢，可以说是从真实的世界得到的灵感。在真实的世界里面，如果曲线是真实的地形。把球从上面滚下来，他滚到plateau的地方呢，不会停下来，因为有惯性，还会往前走。就算是走到上坡的地方，这要这个坡不是很陡，因为惯性的关系，它搞不好还是可以翻过这个山坡，最后就可以走到比当前的local minimum还要好的地方。所以我们要做的事情就是把惯性这个特性塞到gradient descent里面去。这件事情呢，就叫做Momentum。                                         这个东西怎么做呢？ 我们先来复习一下一般的gradient descent。可以看这里。首先计算gradient(红色箭头)，然后沿着反方向（蓝色箭头）走。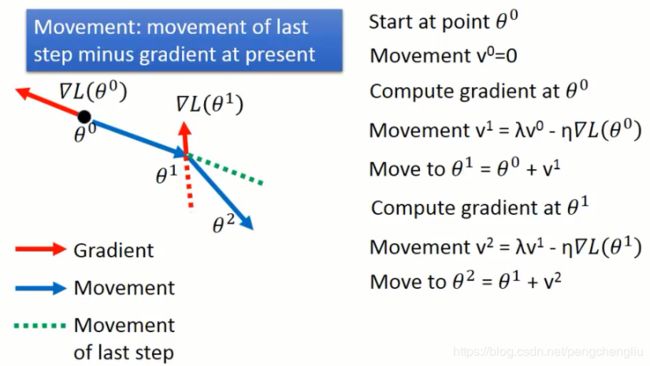                                          当我们加上Momentum的时候，我们是怎么做的呢？加上momentum之后，每次移动的方向不再是只有考虑现在的gradient，而是考虑现在的gradient加上在前一个时间点移动的方向。我们实际来看一下怎么运作的。 首先选一个初始值theta0，然后我们用一个v来记录我们在前一个时间点移动的方向。因为没有初始值，所以v0=0。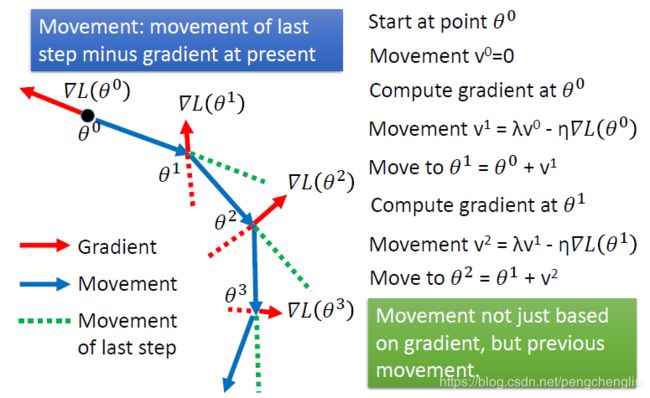                                  接下来计算theta0点的gradient，算出来是红色的箭头。然后呢，现在要移动的方向并不是红色箭头告诉我们的方向，而是前一个时间点的movement v0乘以lambda再加上负的梯度方向，其中lambda表示惯性的影响的大小。然后得到现在要移动的方向v1。这个就好像是惯性一样，如果我们之前走的方向是v0,那今天有一个新的gradient ，并不会让你现在参数更新的方向完全转到gradient的负方向，因为有惯性的关系，你原来走的方向还是有一定程度的影响。我们看下一步可能比较清楚。现在移动的方向是v1。                    再计算theta1处的gradient，接下来要决定说，在第二个时间点我们要走的方向v2是什么样的。我们看图上说，gradient告诉我们要走红色虚线的方向，而原来的方向告诉我们要走蓝色虚线的方向。这两个合起来，就走了新的方向v2。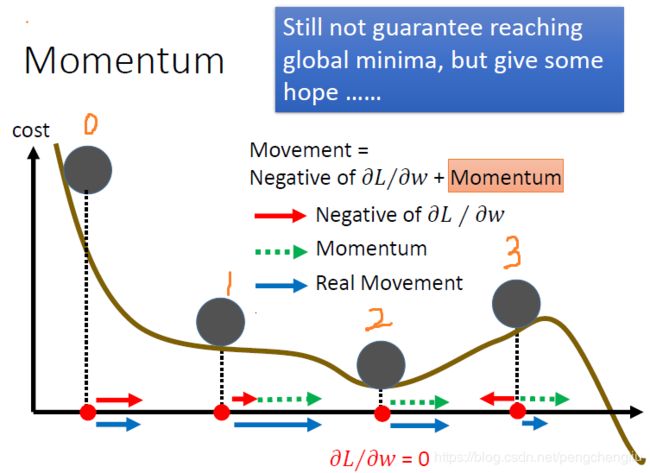                       然后以此类推                      我们可以用另外一个方法来理解这件事情。其实每一个点移动的方向vi，其实是过去所有算出来的gradient的总和。因为带入之后。vi的式子里面有前面的所有的gradient。只是他们的weight是不一样的。lambda设的越小的话，说明越之前的gradient越不去理它，越在意现在的gradient，但是之前的gradient也对update的方向有影响。                                                    如果你看数学式子，不太喜欢的话。可以直观来看一下。到底加入momentum以后，到底是怎么运作的。再加入momentum以后呢，每次移动的方向是负的梯度方向加上momentum建议我们要走的方向。这个momentum其实就是上一个时间点的movement。 所以假设在初试在0位置，gradient建议我们往右走，所以最后就往右移动。 移动到1位置，gradient建议我们往右走，而momentum也建议我们往右走（因为我们是从左边过来的），所以合起来得到蓝色的箭头。 移动到2这个local minimum的地方，gradient为0，gradient告诉说就停在这里。但是momentum告诉你说继续往右走，因为从左边过来的。所以最后参数update的方向会继续向右。 甚至你可以乐观地期待说，今天再往右的时候，走到3这个位置。gradient要求我们向左走。但是momentum建议我们继续向右走。如果今天momentum比较强的话，你就会还是向右走。所以你有可能会跳出local minimum，走到比较好的地方。                                         四、Adam 如果，今天把RMSProp加上Momentum的话，你就得到Adam。看着这个很复杂，但是很多人实现了。 m0就是前一个时间点的momentum。v0就是RMSProp里面的sigma。就是之前的Root Mean Square。 首先算一下gradient gt。根据gt就可以算出新的mt，也就是现在要走的方向。然后再算一下，要放在分母的vt。然后多加了一步，就是做了bias-corrected，至于为什么这么做，可以看paper。最后再更新。 其实不太懂，不过没关系，反正都是用工具，输一条命令而已。