1.概念
凸包(Convex Hull)是一个计算几何(图形学)中的概念。用不严谨的话来讲,给定二维平面上的点集,凸包就是将最外层的点连接起来构成的凸多边型,它能包含点集中所有点的。
这个算法是由数学大师葛立恒(Graham)发明的,他曾经是美国数学学会(AMS)主席、AT&T首席科学家以及国际杂技师协会(IJA)主席。
2.问题
给定平面上的二维点集,求解其凸包。
3.Graham's Scan
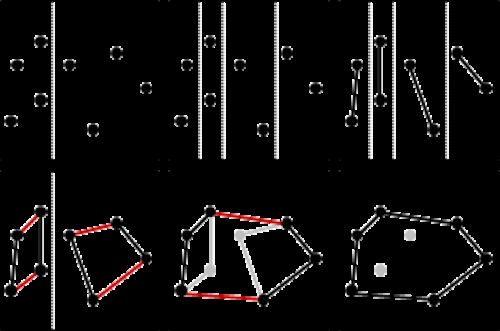
Graham's Scan尝试先将所有点依照时针顺序排好,再来做绕行一圈的动作,绕行途中顺便扫除凸包内部的点,如此就不必以穷举所有点的方式来寻找最外围的点。
要让所有点依照时针顺序排好,只要将中心点设定在凸包内部或者凸包上,然后让各点依照角度排序即可。如果把中心点设定在凸包外部,结果就不见得是时针顺序了。包覆时必须按照时针顺序,才能确保结果正确。
一般来说,选择凸包上的顶点当作中心点是比较好的,因为角度排序时的夹角皆小于180°,可以使用叉积运算来排序(大于180°叉积得负值、等于180°叉积等于零,导致排序错误)。另一个好处是,中心点也可以作为包覆的起点。
角度排序时,遇到角度相同的情况,要小心排序。通常是让距离中心点较近的点排前面。也可以排后面,但是不能乱排。
扫描的过程当中,经常株连许多点。使用stack数据结构来储存凸包,逐一判断stack顶端的点,逐一弹出凹陷的点。凹陷的点必定不是凸包上的顶点。
如果想找出凸包上重迭的点、共线的点,必须特别小心处理刚开始包、快包好时那些重迭的点、共线的点。一种解决方式是:从最低最左点开始,分头往左右两边包,包至最高最右点。相当麻烦。
至于凸包退化成线段或点的情况,则更难解决,此处不讨论。
总而言之,此算法无法漂亮的解决多点共线的问题。
复杂度分析:
这个算法可以直接在原数据上进行运算,因此空间复杂度为O(1)。但如果将凸包的结果存储到另一数组中,则可能在代码级别进行优化。由于在扫描凸包前要进行排序,因此时间复杂度至少为快速排序的O(nlogn)。后面的扫描过程复杂度为O(n),因此整个算法的复杂度为O(nlogn)。
4.Divide and Conquer
分治法的主要区别在Merge的过程,Merge的方法有很多,这里只说其中两种:
4.1找两个凸包的外公切线
一开始将所有点以X坐标位置排序。
Divide:将所有点分成左半部和右半部。
Conquer:左半部和右半部分别求凸包。
Merge:将两个凸包合并成一个凸包。
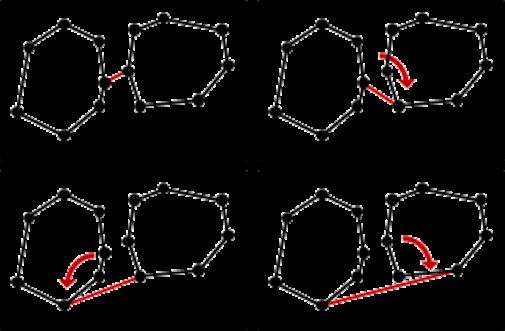
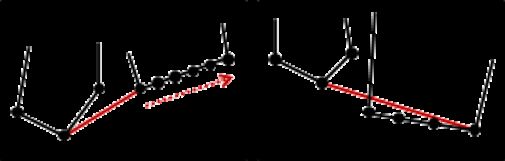
合并凸包,找到两条外公切线即可。从左凸包最右点、右凸包最左点开始,固定左端顺时针转、固定右端逆时针转,轮流前进直到卡死,就得到下公切线,时间复杂度为O(n)。
注意到,下公切线并不见得是左右两凸包的最低点联机,所以就算一开始抓的是左右凸包的最低点,运气不好时,仍需要O(n)时间才能找到下公切线。况且抓最低点有可能已经冲过头了。
正确性证明:找外公切线的过程中绝对不会与两凸包相交、找内公切线的过程中一定会与两凸包相交,卡死时即是相交与不相交的分际,分际即是公切线。
4.2对左右两个凸包上的所有点使用Graham算法
Preprocess: (时间复杂性为O(1))
(1) 如果|Q|<3,算法停止;
(2) 如果|Q|=3,按照逆时针方向输出CH(Q)的顶点;
Divide:(时间复杂性为O(n))
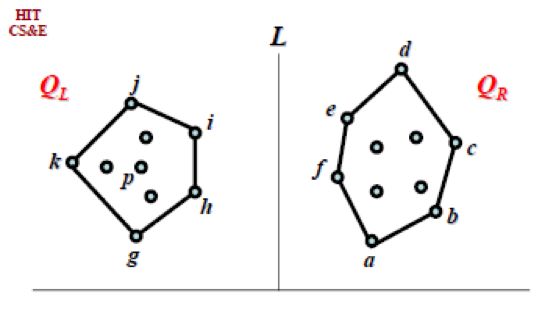
选择一个垂直于x-轴的直线把Q划分为基本相等的两个集合QL和QR,QL在QR的左边;
Conquer:(时间复杂性为2T(n/2))
递归地为QL和QR构造CH(QL)和CH(QR);
3个序列:
合并以后:
Merge:(时间复杂性为O(n))
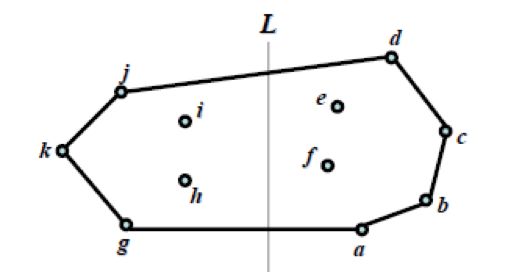
(1) 找一个QL的内点p;
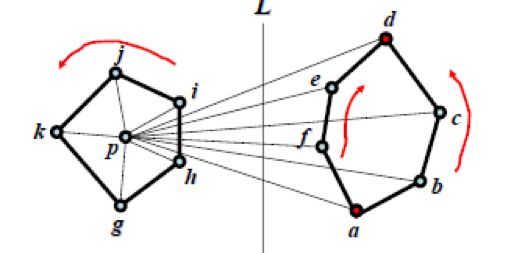
(2) 在CH(QR)中找与p的极角最大和最小顶点u和v;
(3) 构造如下三个点序列:
i. 按逆时针方向排列的CH(QL)的所有顶点,
ii. 按逆时针方向排列的CH(QR)从u到v的顶点,
iii. 按顺时针方向排列的CH(QR)从u到v的顶点;
(4) 合并上述三个序列;
(5) 在合并的序列上应用Graham-Scan.
使用Graham算法递归求左右部分的凸包。这样会过滤掉许多内部点。
QR按顺时针和逆时针分成两部分QR1和QR2(以y最大和y最小的点为界),得到这三个极角有序列表后,合并这三个有序表(merge的操作O(n),原理类似归排的merge)。
对新list直接进行GrahamScan,只需过滤掉极少的点即可得到凸包。
复杂度分析:
一次排序的时间,通常为O(nlogn);Divide and Conquer向下递归O(nlogn)深度,合并凸包需要O(n)时间,总共为O(nlogn)。
一开始可以不必排序,只要把所有点分成两等份即可。两个凸包合并成一个凸包时,两个凸包可能会重迭,仍然可以用O(n)时间解决,不过算法较复杂,此处省略之。
5.参考
Graham's Scan法求解凸包问题
http://www.cnblogs.com/devymex/archive/2010/08/09/1795392.html
Convex Hull
http://www.csie.ntnu.edu.tw/~u91029/ConvexHull.html