Java实现十大排序（动图、代码、注释、链接）

十大经典排序算法

概述

十种常见的排序算法可以分为两类：

• 比较类排序：通过比较来决定元素间的相对次序，由于其时间复杂度不能突破$O(nlogn)$，因此也成为非线性比较类排序。
• 非比较类排序：不通过比较来决定类决定元素间的相对次序，它可以突破基于比较排序的时间下界，以线性时间运行，因此也称为线性时间非比较内排序。

稳定与不稳定：指如果a=b，a原本在b前面，排序后仍在，视为稳定；反之则为不稳定。

时间复杂度：对排序数据的总操作次数。反映当n变化时，操作次数呈现的规律。

空间复杂度：指算法在计算机内执行所需存储空间的度量，也是规律规模n的函数。

排序算法

冒泡排序（Bubble Sort）

依次比较两个相邻的元素，如果它们顺序错误，则将它们位置换过来，这样，最大或者最小的元素就会浮动到两端。

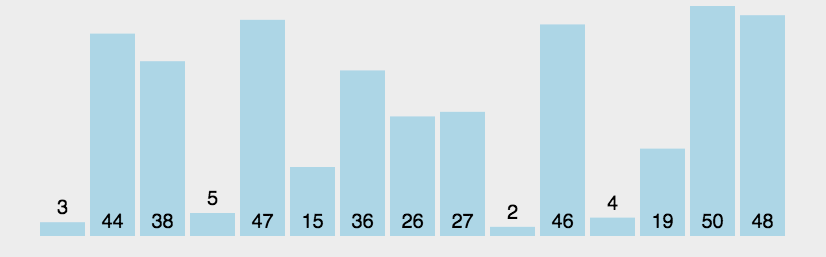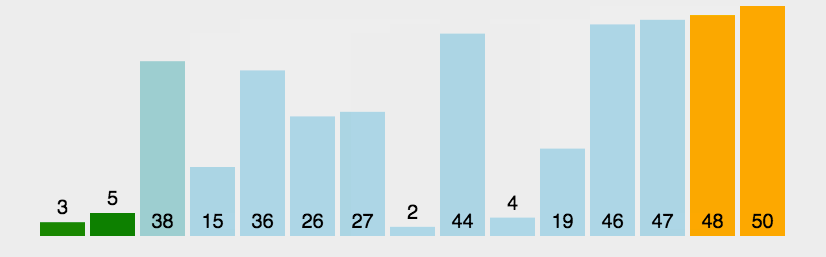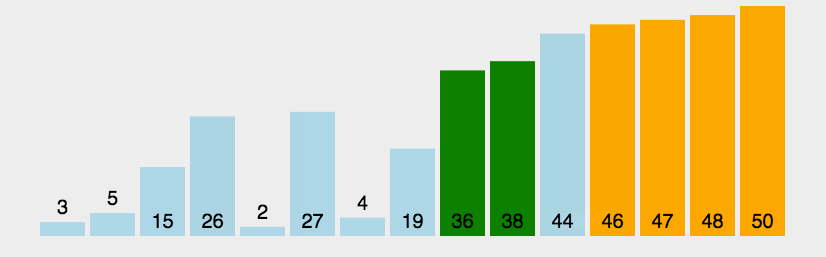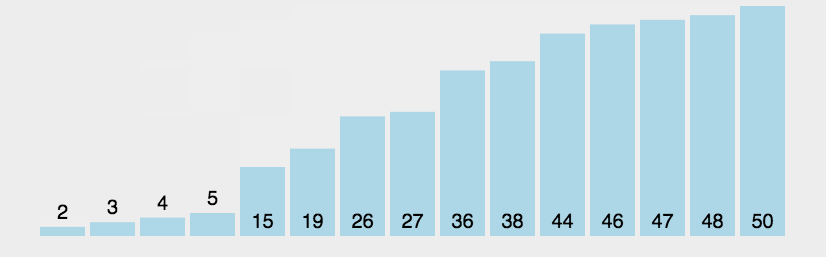
// 辅助代码，后续方法中会继续使用
// 利用异或操作，交换数组中指定角标的元素
private static void swap(int[] arr, int a_index, int b_index){
    if(arr[a_index] == arr[b_index])return;
    arr[a_index] ^= arr[b_index];
    arr[b_index] ^= arr[a_index];
    arr[a_index] ^= arr[b_index];
}

//i循环控制已排序的个数，j循环控制参与排序的元素，由于有j+1，故if判断中-1-i
public static void bubble(int[] arr) {
    for (int i = 0; i < arr.length; i++) {
        for(int j = 0; j < arr.length-1-i; j++){
            //改变正负可改变排序方式；比较的是j与j+1
            if(arr[j] > arr[j+1]){
                swap(arr, j, j+1);
            }
        }
    }
}

选择排序（Selection Sort）

首先从未排序的数组中选出最大/最小的元素，存放到数组的起始位置；然后，从未排序的数组中选出此时最大/最小元素，放入已排序的末尾。以此内推，直至所有元素均排序完毕。

public static void selection(int[] arr) {
    for (int i = 0; i < arr.length - 1; i++) {
        int point = i; // 此处定义最小元素的下标，从该处开始
        for (int j = i+1; j < arr.length; j++) {
            if(arr[point] > arr[j]) point = j; // 找到最小元素的下标
        }
        swap(arr, i, point);
    }
}

插入排序（Insertion Sort）

工作原理是通过构建有序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

public static void insertion(int[] arr) {
    for (int i = 1; i < arr.length; i++) {
        int current = arr[i]; // 必须记录下当前值
        int pre_index = i;
        // 注意while循环中两个判断的位置
        while (pre_index > 0 && current < arr[pre_index - 1]) {
            arr[pre_index] = arr[--pre_index]; // 写法帅气
        }
        arr[pre_index] = current;
    }
}

希尔排序（Shell Sort）

第一个突破$O(n^2)$的排序算法，是简单插入排序的改进版。它与插入排序的不同之处在于，它会优先比较距离较远的元素。希尔排序又称递减增量排序。

希尔排序是把记录按下标的一定增量分组，对每组使用简单插入排序算法排序；随着增量逐渐减少，每组包含的元素越来越多，当增量减至1时，整个区间恰被分为一组，算法便终止。

public static void shell(int[] arr) {
    int len = arr.length;
    for (int step = len / 2; step > 0; step /= 2) {
        for (int i = step; i < len; i++) {
            int current = arr[i];
            int j = i;
            while (j - step >= 0 && current < arr[j - step]) {
                arr[j] = arr[j-step];
                j -= step;
            }
            arr[j] = current;
        }
    }
}

归并排序（Merge Sort）

该算法是分治法(Divide and Conquer)的一个典型应用。先将序列划分为子序列，进行排序；再将已有序的子序列合并，得到完全有序的序列。

分治法：

• 分割：递归地把当前序列平均分割成两半。
• 集成：在保持元素顺序的同时将上一步得到的子序列集成到一起（归并）。

public static void merge(int[] arr, int[] temp, int left, int right) {
    // 在排序前，先建好一个长度等于原数组长度的临时数组，避免递归中频繁开辟空间
    // sort arr
    if (left >= right - 1)
        return;
    int mid = (left + right) / 2; // 求mid注意加法内存溢出错误
    merge(arr, temp, left, mid);
    merge(arr, temp, mid, right);
    // merge arr
    int i = left, j = mid, t = 0;
    while (i < mid && j < right) {
        if (arr[i] < arr[j]) {
            // 数组中的++，先赋值，再+1
            temp[t++] = arr[i++];
        } else {
            temp[t++] = arr[j++];
        }
    }
    while (i < mid)
        temp[t++] = arr[i++];
    while (j < right)
        temp[t++] = arr[j++];
    t = 0;
    // 利用left
    while (left < right)
        arr[left++] = temp[t++];
}

快速排序（Quick Sort）

基本思想：通过一趟排序将待排记录分隔成独立的两部分，其中一部分记录的关键字比另一部分小；再分别对这两部分记录进行排序，以达到整个序列有序。

算法描述：

快速排序使用分治法把一个序列分为两个序列。具体算法描述如下：

• 从数列中挑出一个元素，成为“基准“(pivot)；
• 排序数列，所有比基准小的摆放到基准左边；大的右边。在这个分区退出之后，基准就处于数列的中间位置。
• 递归把小于基准、大于基准的子数列进行排序。基准不参与排序；直至子串长度为1，结束递归。

public static void quick(int[] arr, int left, int right) {
    if (left >= right - 1)
        return;
    int pivot = arr[left]; // 将最左边元素作为基准
    int i = left;
    for (int j = left + 1; j < right; j++) {
        // 交换符号，可改变排序顺序
        if (arr[j] < pivot) {
            swap(arr, j, ++i);
        }
    }
    swap(arr, left, i); // 将基准元素换到中间去
    quick(arr, left, i);
    quick(arr, i + 1, right);
}

堆排序（Heap Sort）

堆排序是利用堆这种数据结构设计的一种排序算法，是一种选择排序。

堆是具有以下性质的完全二叉树：

• 每个结点的值都大于或等于其左右孩子结点的值，称为大顶堆（Max-Heap）；
• 或者每个结点都小于等于其左右孩子结点的值，称为小顶堆（Min-Heap)。

堆节点访问：

• 父节点i的左子节点在位置$(2i+1)$
• 父节点i的右子节点在位置$(2i+2)$
• 子节点i的父节点在位置$floor((i-1)/2)$

代码思路：

1. 将无序队列构建成一个堆，根据升序降序需求选择大顶堆或者小顶堆；
2. 将堆顶元素与末尾元素交换，将最大元素“沉”到数组末端；
3. 重新调整结构，使其满足堆定义，然后继续交换堆顶元素与当前末尾元素，反复执行调整+交换步骤，直到整数序列有序。

![在这里插入图片描述

// 参考代码 https://zh.wikipedia.org/wiki/%E5%A0%86%E6%8E%92%E5%BA%8F#Java
public static void heap(int[] arr) {
    // 1. 将数组堆化，buildHeap
    int len = arr.length - 1;
    int beginIndex = (len - 1) >> 1;
    for (int i = beginIndex; i >= 0; --i) {
        maxHeapify(i, len, arr);
    }
    // 2. 对堆化数据排序，每次都输移出最顶层的根节点，与其最尾部节点位置调换
    for (int i = len; i > 0; i--) {
        swap(arr, 0, i);
        maxHeapify(0, i-1, arr);
    }
}
// 调整索引为index出的数据，使其符合堆的特性
private static void maxHeapify(int index, int len, int[] arr) {
    int left = (index << 1) + 1; // 左子节点索引
    int right = left + 1;
    if (left > len) return; // 左节点超过长度，退出
    int max = left;
    // 右节点超出，就只判断左节点
    if(right <= len && arr[right] > arr[left]) max = right;
    if(arr[index] < arr[max]) {
        swap(arr, index, max); // 如果父节点被子节点调换，
        maxHeapify(max, len, arr); // 则继续判断换下后的父节点是否符合堆的特性
    }
}

计数排序（Counting Sort）

计数排序使用一个额外的数组$C$，其中第i个元素是待排序数组$A$中值等于$i$的元素的个数。然后根据数组$C$来将$A$中的元素排到正确的位置。$C$的长度取决于待排序数组中数据的范围（等于最大值与最小值的差加上1）。

由于用来计数的数组$C$的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上1），这使得计数排序对于数据范围很大的数组，需要大量时间和内存。

计数排序是用来排序0到100之间的数字的最好的算法。

算法步骤如下：

1. 找出待排序的数组中最大和最小元素
2. 统计数组中每个值为$i$的元素出现的次数，并存入数组$C$的第$i$项
3. 反向填充目标数组：将每个元素$i$放在新数组的第$C[i]$项，每放一个元素，就将$C[i]$减$1$

public static void counting(int[] arr) {
    // 获取最大最小值
    int max = arr[0], min = arr[0];
    for (int i = 0; i < arr.length; i++) {
        if (arr[i] > max) max = arr[i];
        if (arr[i] < min) min = arr[i];
    }
    // 创建计数数组C，并进行计数操作
    int[] c = new int[max-min+1];
    for (int i = 0; i < arr.length; i++) {
        c[ arr[i] - min ] ++ ;
    }
    // 反向填充目标数组
    int cnt = 0; // 利用计数器可以省略对数组c的累加操作，c[i] += c[i-1]，无法保证稳定性
    for (int i = 0; i < c.length; i++) {
        while (c[i] != 0) {
            arr[cnt++] = i + min;
            c[i] -- ;
        }
    }
}

桶排序（Bucket Sort）

桶排序是计数排序的升级版。它利用了函数的映射关系，高效与否的关键就在于映射函数。

原理：假设输入的数据服从均匀分布，将数据分到有限数量的桶里，每个桶再分别排序（有可能再使用别的排序算法或是以递归的方式继续使用桶排序）。

算法步骤：

1. 设置一个定量的数组当作空桶
2. 寻访序列，并且把数据一个一个放到对应的桶子里
3. 对每个不是空的桶子进行排序
4. 从不是空的桶子里把数据再放回到原来的序列中

public static void bucket(int[] arr) {
    // 1. 求最大值，用于求最大值的位数
    int max = arr[0], min = arr[0];
    for (int i = 0; i < arr.length; i++) {
        max = Math.max(max, arr[i]);
        min = Math.min(min, arr[i]);
    }
    // 2. 设置桶
    int bucketNum = max / 10 - min / 10 + 1; // 数量，映射函数
    // 创建桶
    List<List<Integer>> buckets = new ArrayList<>();
    for (int i = 0; i < bucketNum; i++) {
        buckets.add(new ArrayList<Integer>());
    }
    // 放入元素
    for (int i = 0; i < arr.length; i++) {
        buckets.get(arr[i] / 10 - min / 10).add(arr[i]);
    }
    // 3. 对每个非空桶中元素进行排序
    int index = 0; // 4. 赋值给arr
    List<Integer> bucket = new ArrayList<>();
    for (int i = 0; i < bucketNum; i++) {
        bucket = buckets.get(i);
        if(bucket.size() != 0){
            insertSort(bucket);
            for (int j = 0; j < bucket.size(); j++) {
                arr[index++] = bucket.get(j);
            }
        }
    }
}
// 对每个非空桶中元素进行排序
private static void insertSort(List<Integer> list) {
    for (int i = 1; i < list.size(); i++) {
        int cur = list.get(i);
        int pre = i;
        while (pre > 0 && cur < list.get(pre-1)) {
            list.set(pre, list.get(--pre));
        }
        list.set(pre, cur);
    }
}

基排序（Radix Sort）

原理：将整数按位数切割成不同的数字，然后按每个位数分别比较。

具体实现：将所有待比较数值（正整数）统一为同样的数字长度，数字较短的数前面补零。然后从最低位开始，依次进行排序。这样从最低位排序一直到最高位排序完成后，数列就变成了一个有序序列。

public static void radix(int[] arr) {
    int mod = 10, dev = 1; // 用于求每位的值
    // 求最大值，用于求最大值的位数
    int max = arr[0];
    for (int i = 1; i < arr.length; i++) {
        max = Math.max(max, arr[i]);
    }
    int maxDigit = 1; // 最大位数
    while (max > mod) {
        max /= 10;
        maxDigit ++ ;
    }
    // 对每一位进行排序
    for (int i = 0; i < maxDigit; i++, dev *= 10) {
        // 采用计数排序
        int[] cnt = new int[10];
        // 计数排序的第二种方法，利用新的数组记录arr值
        int[] temp = new int[arr.length]; 
        for (int j = 0; j < arr.length; j++) {
            int cn = (arr[j] / dev) % mod;
            cnt[cn] ++ ;
        }
        for (int j = 1; j < cnt.length; j++) {
            cnt[j] += cnt[j-1];
        } // 从小到大
        // for (int j = cnt.length-2; j >=0; --j) {
        //     cnt[j] += cnt[j+1];
        // } // 从大到小
        for (int j = arr.length-1; j >= 0; --j) {
            temp[-- cnt[(arr[j] / dev) % mod]] = arr[j];
        } // 必须从后往前遍历，记录第一轮顺序
        // 将temp赋值给arr
        for (int j = 0; j < arr.length; j++) {
            arr[j] = temp[j];
        }
    }
}

注意：内部排序使用的是计数排序。注意此处与之前计数排序算法的区别。上述计数排序利用一个cnt记录元素个数，这样得到的结果不满足稳定性。第二种方法，通过从后往前给temp赋值，之前在后面的元素，赋值到temp中还在后面（体现在-- cnt[index]）。

LeetCode题解

TopK问题

利用堆来实现。小顶堆解决最大k个数问题；大顶堆解决最小k个数问题。

自定义堆，在堆排的基础上稍作修改，buildHeap与heapify函数都是一样的实现，不难理解。

思路：堆排利用的大（小）顶堆所有子节点元素都比父节点小（大）的性质来实现。这里故技重施，既然一个小顶堆的顶是最小的元素，那么我们要找最大的k个元素，是不是可以建立一个包含k个元素的堆，然后遍历集合，如果集合的元素比堆顶的元素大（说明它目前应该在k个最大之列），那么就用该元素来替换堆顶元素，同时继续维护堆的性质，那么在遍历结束的时候，堆中包含的k个元素就是我们要找的k个最大的元素，其中堆顶元素是第k大的元素，小于其子节点k-1个元素。

public static int topk2(int[] arr, int k) {
    int[] heap = new int[k];
    for (int i = 0; i < k; i++) {
        heap[i] = arr[i];
    }
    int len = k - 1;
    int index = (len - 1) >> 1;
    for (int i = index; i >= 0; --i) {
        minHeapify(i, len, heap); // 注意，传进来的数组是heap
    }
    for (int i = k; i < arr.length; i++) {
        if(arr[i] > heap[0]){
            heap[0] = arr[i];
            minHeapify(0, len, heap);
        }
    }
    return heap[0];
}
// 小顶堆
private static void minHeapify(int index, int len, int[] arr) {
    int left = (index << 1) + 1;
    int right = left + 1;
    if(left > len) return;
    int min = left;
    if(right <= len && arr[right] < arr[min]) min = right;
    if(arr[min] < arr[index]){
        swap(arr, index, min);
        minHeapify(min, len, arr);
    }
}

利用优先级队列，该队列内部实现了堆

思路：先利用堆维护扫描到的前k个数，其后每一次扫描到元素，若大于堆顶，则入堆，然后删除堆顶；依此往复，直至扫描完所有元素。

public static int topk(int[] arr, int k) {
    PriorityQueue<Integer> pq = new PriorityQueue<>();
    for (int num : arr) {
        if(pq.size() < k || num > pq.peek()) pq.offer(num);
        if(pq.size() > k) pq.poll();
    }
    return pq.peek();
}

利用快速排序

利用快排的思想来解决TopK问题，必然要用到分治法

思路：

Quick Select的目标是找出第k大元素，所以

• 若切分后的左子数组的长度 > k，则第k大元素必出现在左子数组中；
• 若切分后的左子数组的长度 = k-1，则第k大元素为pivot；
• 若上述两个条件均不满足，则第k大元素必出现在右子数组中。

思路2，topk4方法。分治函数会返回一个position，在position左边的数都比第position个数小，在position右边的数都比第position大。我们不妨不断调用分治函数，直到它输出的position = K-1，此时position前面的K个数（0到K-1）就是要找的前K个数。

public static int topk3(int[] arr, int k) {
    return quickSelect(arr, k, 0, arr.length-1);
}
// quickSelect
private static int quickSelect(int[] arr, int k, int left, int right) {
    if(left == right) return arr[left];
    int position = position(arr, left, right);
    if(position - left == k - 1) return arr[position];
    else if (position - left > k - 1) return quickSelect(arr, k, left, position-1);
    else return quickSelect(arr, k-1-position+left, position+1, right);
}
// 不改变k个大小，始终根据返回的position值判断
public static int topk4(int[] arr, int k) {
    int position = position(arr, 0, arr.length-1);
    while (position != k - 1) {
        if(position > k - 1) position = position(arr, 0, position-1);
        if(position < k - 1) position = position(arr, position+1, arr.length-1);
    }
    return arr[k-1];
}
// getPosition
private static int position(int[] arr, int left, int right) {
    int pivot = arr[left];
    int position = left;
    for (int i = left+1; i <= right; i++) {
        if(arr[i] > pivot){
            swap(arr, i, ++position);
        }
    }
    swap(arr, position, left);
    return position;
}