海量数据挖掘MMDS week2: 局部敏感哈希Locality-Sensitive Hashing, LSH
http://blog.csdn.net/pipisorry/article/details/48858661
海量数据挖掘Mining Massive Datasets(MMDs) -Jure Leskovec courses学习笔记之 Locality-Sensitive Hashing(LSH) 局部敏感哈希
LSH第一部分。第二部分参考[海量数据挖掘MMDS week7: 局部敏感哈希LSH(进阶)]
局部敏感哈希LSH简介
LSH聚焦在很可能相关的事物上,而避免对不可能是我们想要查找的事物进行检测,这个和原始的hash有一定相似,也就是直接查找到我们想要的记录而不用遍历整个数据集。A fundamental problem of scale: If we have even a million sets, the number of pairs of sets is half a trillion.We don't have the resources to compare them all, so we need some magic defor,focus us on the pairs that are likely to be highly similar,never looking at the vast majority of pairs.
shingling, a way to convert the informal notion of similar documents into a formal test for similarity of sets.
min hashing, allows us to replace a large set by a much smaller list of values.the similarity of the small lists,called signatures,predicts the similarity of the whole sets.
locality sensitive hashing,is another bit of magic.we are pointed right at the similar pairs without having to wade through the morass of all pairs.find similar sets or similar documents without doing anything that involves searching all pairs.
哈希
hash的查找时间复杂度是O(1),有着极高的查找性能。
我们通常的哈希,比如有一个hash function: f(x)=(x*7)%10,有两个数据x1=123,x2=124,现在用f(x)把它们hash一下,f(x1)=1,f(x2)=8,这想说明什么呢?看看原来的数据,是不是很相似?(假设用欧氏距离度量)再看hash后的数据,那就差得远了,说明这个hash它并没有保持相似性,那么这种就不是局部敏感哈希。
局部敏感哈希LSH
那什么叫“局部敏感”的哈希?它的意思就是:如果原来的数据相似,那么hash以后的数据也保持一定的相似性。LSH在hash之后能保持一定的相似性,这里为什么说是“保持一定的相似性”?我们知道,hash函数的值域一般都是有限的,但是要哈希的数据却是无法预知的,可能数据大大超过其值域,那么就不可能避免地会出现一个以上的数据点拥有相同的hash值。假设有一个很好的hash function,好到可以在hash之后很好地保持原始数据的相似性,假设它的不同取值数是10个,然后现在我有11个截然不相似的数据点,想用这个hash function来hash一下,必然会出现一个hash桶中有1个以上的数据点,只能在hash之后保持一定的相似性。其根本原因就是在做相似性度量的时候,hash function通常是把高维数据映射到低维空间上,高维空间上计算复杂度太高。
LSH是如何做的?
LSH思想一句话总结:它是用hash的方法把数据从原空间哈希到一个新的空间中,使得在原始空间的相似的数据,在新的空间中也相似的概率很大,而在原始空间的不相似的数据,在新的空间中相似的概率很小。
在用LSH前通常会进行一些降维操作
整个流程:一般的步骤是先把数据点(可以是原始数据,或者提取到的特征向量)组成矩阵,然后通过第一步的hash functions(有多个哈希函数,是从某个哈希函数族中选出来的)哈希成一个“签名矩阵(Signature Matrix)”,这个矩阵可以直接理解为是降维后的数据;然后再通过LSH把Signature Matrix哈希一下,就得到了每个数据点最终被hash到了哪个bucket里;如果新来一个数据点,假如是一个网页的特征向量,我想找和这个网页相似的网页,那么把这个网页对应的特征向量hash一下,看看它到哪个桶里了,于是bucket里的网页就是和它相似的一些候选网页,这样就大大减少了要比对的网页数,极大的提高了效率。
皮皮blog
寻找相似集
集合相似性的应用及需求
Note: entity resolution实体分辨: People create records of data about themselves at many different sites,Google, Amazon, Facebook and so on.We may want to figure out when two records refer to the same individual. 右图:相似文档。
寻找相似集的Outline
文档相似性度量的三大基本技术
shingling是将文档转换为可用于比较的string集合(或者进一步tokens)的矩阵。
minhashing是在保持文档相似性的基础上,对原始shinglings矩阵进行压缩,压缩文档的维度,变成signatures矩阵。得出的结果其实可以直接计算文档相似度了,不过为了进一步减少比较次数从而减少计算量要再使用lsh。The result of minhashing a set is a short vector of integers.The key property,which we'll prove, is that the number of components in which the two of these vectors agree is the expected value of the similarity of the underlying sets. minhash的主要作用:the reason we want to replace sets by their signatures is that the signatures take up much less space.we'd like to be able to work in main memory.
lsh是选出需要比较的文档(相似性较高的),形成候选对的才进行比较,减少需要比较的文档signatures数目。当然使用lsh可以不用minhashing阶段,直接使用shinglings,不过大多时候使用minhashing比较量会减少很多。
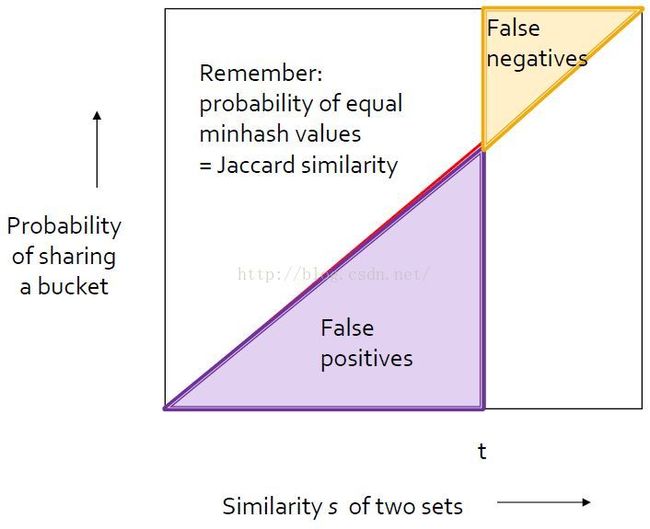
Note: 从上可知,LSH整个方法存在false positives 和 false negatives,但是我们可以通过小心选择使用的参数,可以让false的概率变得足够小。
皮皮blog
Shingles文档表示
将原始文档进行表示和转换,转换成文档-shingles(列-行)矩阵。Shingling是我们将文档转换成集合的方法,这样有很多text相同的文档会被转换成有很多元素members相同的集合。
shingles相关概念
k-shingle(k-gram): 文档中k个consecutive(连续的) 字符序列。
字符characters: 空白符也当成字符,但是html文档可以保留也可以去掉一些tag字符。The blanks that separate the words of the document are normally considered characters. If the document involves tags such as an HTML document then the tags may also be considered characters or they can be ignored.
空白串的处理:对于空白串(空格、tab及回车等)的处理存在多种策略。将任意长度的空白串替换为单个空格或许很合理,采用这种做法,会将覆盖2个或更多词的shingle和其他shingle区分开来。
Note: 这里同一文档中的shingles只计数一次,所以后面的相似性度量是使用Jaccard相似性。
shingles大小k的选择
k的取值: k一般取值在5 - 10。k应该选择得足够大,以保证任意给定的shingle出现在任意文档中的概率较低。
如邮件文档取k=5,而研究论文一样的大文档选择k=9。也就是越可能出现shingle相似的文档,k应该取更大些。
k-shinglings示例
shingles保持文档相似性的intuition
将文档表示成shingles仍然可以让我们检测到直观上(intuitively)相似的文档对。
进一步Shingles还可以hash压缩表示成tokens
我们构造shingle集合然后hash每个shingles得到新的shingles,一般称为token。
将shingles压缩成tokens的好处:
一个原因是:大多的k-shingles在文档中不出现,压缩之后这些k-singles也不会有太大的冲突(哈希冲突:几乎不发生。There's a small chance of a collision where two shingles hashed to the same token, but that could make two documents appear to have shingles in common when in fact they have different shingles.But such an an occurrence will be quite rare),大多tokens还是不会出现在文档中,对相似性的度量影响不大但是却可以节省太多空间。Because documents tend to consist mostly of the 26 letters(或者256个字符), and most shingles do not appear in a document,we are often forced to use a large value of k, like k = 10. But the number of different strings of length ten that will actually appear in any document is much smaller than 256^10 or even 26^10.Thus, it common to compress shingles to save space while still preserving the property that most shingles do not appear in a given document.
另一个原因是:Shingling方法里的k值比较大时,可以对每个片段进行一次hash。比如k=9,我们可以把每个9字节的片段hash成一个32bit的整数。这样既节省了空间又简化了相等的判断。这样两步的方法和4-shingling占用空间相同(共有文档字符个数N个9-shingling或者4-shingling,但是9-shingling占用9bytes,而4-shingling只占用4bytes = 32bits),但是会有更好的效果。因为字符的分布不是均匀的,在4-shingling中实际上大量的4字母组合没有出现过,而如果是9-shingling再hash成4个字节就会均匀得多。Since documents are much shorter than 2^32 byte, we still can be sure that a document is only a small fraction of the possible tokens in it's sets.
皮皮blog
Minhashing 压缩featutes
在有些情况下我们需要用压缩的方式表示集合,但是仍然希望能够(近似)计算出集合之间的相似度,也就是通过Minhashing方法压缩文档-shingles(列-行)矩阵 为 文档-signatures矩阵后再进行文档相似性比较。
Note: 针对不同的相似度测量方法,局部敏感哈希的算法设计也不同:使用Jaccard系数度量数据相似度时的min-hash,使用欧氏距离度量数据相似度时的P-stable hash。[http://blog.sina.com.cn/s/blog_67914f2901019p3v.html]
文档的布尔矩阵表示及Jaccard相似性
Jaccard similarity相似性
文档shingles的集合表示到布尔矩阵表示
universal set:如果集合来自k-shingling文档,则the universal set就是所有K字符或者K tokens序列的所有可能集合。
布尔矩阵:每行即属性(K字符或者K tokens序列),每列即集合/文档。
两列(两文档/集合)的Jaccard similarity
两列有4种不同类型的行abcd
文档shingles的minhash压缩表示-签名矩阵signature matrix
signature: 对每一列,signature就是通过轮流应用这些minhash函数到这些列column得到的行号的序列sequence。
设计多个哈希函数,每个hash函数对所有列进行一次hash,如hash列C得到列 C对应的hash值 {而hash列C的hash值等价为:对所有行随机排列后,列C第一个值为1的那一行的行号。这个看上去跟hash没关系?对,没关系,但是这个行号可以通过hash模拟实现,在实际编程中就是使用hash函数hash得到的},这样每个hash函数hash所有列就可以得到新的一行,即所有列的signature表示。重复上述过程,使用k个hash函数对所有列进行hash,就可以得到一个k行的signature矩阵,这个矩阵就是原有矩阵的压缩表示。
故minhash的思想应该就是相似的两列经过多个hash函数hash得到相同hash值的概率如果能保证比不相似的两列大得多,那么minhash后的列signature能保持一定的相似性不变。所以重点在于如何hash才能有这样的保证?
Note:
1 行号可以从0或1开始,结果好像不一样,但都可以。建议如mmds书,从0开始。
2 每一个Minshashing hash函数是和矩阵行的排列permutation关联在一起的,hash函数数目一般选择100个左右。并且对整个矩阵我们选择minhash函数一次并应用同一个minhash函数到每一列中。
下面的示例将会解释 具体minhash是怎么做的?为什么minhash后文档/集合的相似性会保持?
Minhashing示例
假设现在有4个网页(document),页面中词项的出现情况用以下矩阵来表示,1表示对应词项出现,0则表示不出现。
minhash的目标
接下来我们就要去找一种hash function h(),使得在hash后尽量还能保持这些documents之间的Jaccard相似度。目标就是找到这样一种哈希函数h(),如果原来documents的Jaccard相似度sim(C1, C2)高,那么它们的hash值相同h(C1)=h(C2)的概率高,如果原来documents的Jaccard相似度低,那么它们的hash值不相同h(C1)≠h(C2)的概率高。
Min-hashing的定义和获得

首先生成一堆随机置换,把Signature Matrix的每一行进行置换,然后hash function就定义为把一个列C hash成置换后的列C上第一个值为1的行的行号(这里的hash仅仅是一个排列+选择,如何使用真正的hash函数模拟这种排列+选择见下面它的具体实现)。
图中展示了三个置换(彩色的那三条)。比如现在看蓝色的那个置换,置换后的Signature Matrix(不用真的置换,使用索引就OK)为:
然后看第一列的第一个是1的行是第2行,第二列的第一个是1的行号是2, 同理再看三四列,分别是2,1,因此这四列(document)在这个置换下,被哈希成了2,1,2,1,对应图右图蓝色部分,也就相当于每个document现在是1维的。再通过另外两个置换然后再hash,又得到右边的另外两行,于是最终结果是每个document从7维降到了3维。也就是说最后通过minhash,我们将input matrix压缩成了n个维度(n为minhash函数个数)。注意,每置换(排列)对应生成签名矩阵的一行。
[MinHashing基本原理]
Minhashing的性质
为什么minhash后文档/集合的相似性会保持?对于两个document,在Min-Hashing方法中,它们hash值相等的概率等于它们降维前的Jaccard相似度,也就是说在signature矩阵中计算两列的相似度约等于在原有shingles矩阵两列的相似度。
Minhashing性质的证明
如果C1、C2在某个排列(置换)中遇到的第一个非0行是类型a <1,1>的行,那么C1、C2的minhash值相同。否则C1、C2对应的minhash值不同(也就是仍然是类型a的行在控制两列C1C2之间的相似度)。
同一行的两个元素的情况有三种:a.两者都为1;b+c.一个1一个0;d.两者都为0。
一方面,易知原始两列间的Jaccard相似度为a/(a+b+c)。
另一方面,两列的minhash值相同的概率是abc类型的行中类型a占的概率,若排列(置换)是等概率的,则第一个出现的a出现在b+c之前的概率也为a/(a+b+c),而只有这种情况下两集合的minhash值才相同。Thus the probability that the two columns will have the same MinHash value is the probability that the first row that isn't of type-d is a type-a row.That probability is the number of type-a rows divided by the number of rows of any of the types a, b or c.That is, a/(a+b+c).证毕。
这标志着我们找到了需要的hash function。于是方法就有了,我们多次抽取随机排列得到n个minhash函数h1,h2,…,hn,依此对每一列都计算n个minhash值。对于两个集合,看看n个值里面对应相等的比例,即可估计出两集合的Jaccard相似度。可以把每个集合的n个minhash值列为一列,得到一个n行C列的签名矩阵。因为n可远小于R,这样我们就把集合压缩表示了,并且仍能近似计算出相似度。
Note: 现在这个hash function只适用于Jaccard相似度,并没有一个万能的hash function。
Minhashing的严格证明
设有一个词项x(就是Signature Matrix中的行上的值),它满足下式:
就是说,词项x被置换之后的位置,和C1,C2两列并起来(就是把两列对应位置的值求或)的结果的置换中第一个是1的行的位置相同。(π是一个随机排列)
那么有下面的式子成立:
就是说x这个词项要么出现在C1中(就是说C1中对应行的值为1),要么出现在C2中,或者都出现。这个应该很好理解,因为那个1肯定是从C1,C2中来的。
那么词项x同时出现在C1,C2中(就是C1,C2中词项x对应的行处的值是1)的概率,就等于x属于C1与C2的交集的概率。
那么现在问题是:已知x属于C1与C2的并集,那么x属于C1与C2的交集的概率是多少?其实就是看看它的交集有多大,并集有多大,那么x属于并集的概率就是交集的大小比上并集的大小,而交集的大小比上并集的大小,就是Jaccard相似度,于是有下式:
签名signatures的相似度
通过minhash压缩得到的signatures矩阵计算文档/集合的相似度,两列的相似度就是两列中行数值相同的比例。
如果我们使用several hundred Minhash函数,这样可以得到足够小的standard deviation来估计原始的jaccard相似性。
降维后的相似度
右下角那个表给出了降维前和降维后的document两两之间的相似性的对比。在原来的Input matrix矩阵中,列col1和col3的相似度为0.75,而在minhashing后的signature matrix矩阵中,列sig1和sig3的相似度为0.67。以此类推。原本就没有相似性的两列,minhashing后也不可能有,如列1、2。It turns out that when the similarity is zero it is impossible for any min hash function to return the same value for these two columns. 可以看出,使用signature矩阵代替input矩阵计算文档间相似度还是挺准确的。
Minhashing的实现
在具体的计算中,可以不用(也不大可能实用)真正生成随机排列,只要有一个hash函数从[0..R-1]映射到[0..R-1]即可。因为R是很大的,即使偶尔存在多个值映射为同一值也没大的影响。
随机排列的模拟实现
模拟实现排列而不实际对行进行排列。每个main hash函数hash整数值到一些buckets中。假设行R在排列中的位置是H(R),其中H是一个hash函数。这样,对每一列,我们寻找行r将r作为signature值,其中行r在这列中的值为1,且h(r)的值是最小的。每次hash,同一个h()函数hash行r得到的值不同,相当于对行进行了一次随机排列。而每一次hash,第一个碰到的列号模拟成对列c上值为1的所有行号最小的hash值作为h(c)的值,相当于使用hash函数对rows进行了排列。当然实际实现时,可以一行一行处理,而不用一次性将h()对所有行进行hash,而是一次hash一行,如果碰到1而其h(r)比现在signature对应的数小,则替换就可以了,具体看下面的示例1。同时,使用不同的hash函数得到signature也不同,记录下signature矩阵不同行上。
那么,每个hash函数hi()相当于一次不同的排列,我们要计算所有列c的最小哈希minhash值,得到一个M矩阵,其中M(i,c)表示第i个hash函数hash得到的列c列号随机排列后值1对应的最小行号,如果有100个minhash函数,那么slots的维度就是100*列c的数目。具体来说见下图:
Note: 可能的冲突:It's Entirely possible that h_i, maps two or more rows to the same designation.But if we make the number of buckets into which h of i hash is very large,larger than the number of rows,then the probability of a collision at the smallest value is very small, and we can ignore the probability of a collision.
Min-Hashing简易算法
M初始化为无穷大
lz认为上面的算法只是其中一种,只要遍历了所有的行和hash函数,M中的值记录的是最小的那个hash值算法就是可以了。
要注意的是每个h(i,r)只需要计算一次,所以在算法中在每行迭代开始时都先计算好h(i,r),在下面的内循环中重复使用。我们只需要在每行对每个hash函数计算h(r)一次(It is important we compute h(r) only once for each hash function in each row)。
Min-Hashing算法实现实例1
下面选取的hash函数将整数映射到5个桶buckets中(桶初始为无穷大)。
行1的分析: 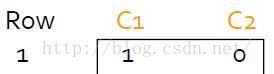 对应的是
对应的是 ,故只更新了sig1(由于row 1 第二列值为0,所以sig2值不变,仍为无穷大)。
,故只更新了sig1(由于row 1 第二列值为0,所以sig2值不变,仍为无穷大)。
所有row遍历完后,sig1的第1个值应该是h(r)最小的行号r,所以每次计算新的h(r)时,如果碰到1,总是将更小的r值替换当前r值。
从上面结果看出,两个signatures在两个componets上都不同,所以估计的列之间的Jaccard相似度为0,同时两列真实的Jaccard相似度为1/5。
Min-Hashing算法实现实例2
Exercise 3.3.3 : InFig. 3.5 is a matrix with six rows.
(a) Compute the minhash signature for each column if we use thefollowing three hash functions: h1(x) = (2x + 1) mod 6; h2(x) = (3x + 2) mod 6; h3(x) = (5x + 2) mod 6.
(b) Which of these hash functions are true permutations(行号经过变换后还是一个完整的序列)?
a) 每次行迭代产生的新signatures为:
row0:
[[10 1 10 1]
[10 2 10 2]
[10 2 10 2]]
row1:
[[10 1 10 1]
[10 2 10 2]
[10 1 10 2]]
row2:
[[ 5 1 10 1]
[ 2 2 10 2]
[ 0 1 10 0]]
row3:
[[5 1 1 1]
[2 2 5 2]
[0 1 5 0]]
row4:
[[5 1 1 1]
[2 2 2 2]
[0 1 4 0]]
row5:
[[5 1 1 1]
[2 2 2 2]
[0 1 4 0]]
最终得到的minhash signatures结果为:
|
|
S1 |
S2 |
S3 |
S4 |
| 0 |
5 |
1 |
1 |
1 |
| 1 |
2 |
2 |
2 |
2 |
| 2 |
0 |
1 |
4 |
0 |
b)
不同hash函数对行号的hash值为:
|
|
h1(x) = (2x + 1) mod 6 |
h2(x) = (3x + 2) mod 6 |
h3(x) = (5x + 2) mod 6 |
| 1 |
3 |
5 |
1 |
| 2 |
5 |
2 |
0 |
| 3 |
1 |
5 |
5 |
| 4 |
3 |
2 |
4 |
| 5 |
5 |
5 |
3 |
| 0 |
1 |
2 |
2 |
从表中看出只有h3(x) = (5x + 2) mod 6是真的排列hash函数。
minhash程序实现python代码:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
"""
__title__ = '局部敏感哈希LSH'
__author__ = '皮'
__mtime__ = '6/1/2016-001'
__email__ = '[email protected]'
"""
实现过程要注意的地方
Note:The algorithm we describe as soon as we can visit the matrix row by row.But often the data is available by columns and not by rows.For instance,if we have a file of documents,it's natural to process each document once, computing its shingles.That, in effect,gives us one column of the matrix.
Start with a list of row column pairs where the ones are.Initially sort it by column,and sort these pairs by row.
[Locality Sensitive Hashing 详解]
皮皮blog
局部敏感哈希Locality-Sensitive Hashing,LSH
LSH基本思想
上面通过minhash降低了文档相似性比较复杂度(features减少了),但是即使文档数目很少,需要比较的数目可能还是相当大。所以要生成候选对,只有形成候选对的两列才进行相似度计算,相似度计算复杂度又降低了。
基本思想::只有两列有比例fraction t的元素是一样的才当成一个candidate pair。列c和d要成为候选集,其signatures相同比例至少为t,也就是signatures矩阵中行相同的个数即M(i,c)=M(i,d)的数目占的比例至少为t。threshold t是成为候选集的最小阈值。我们想要达到的目的是:保证相似的列(signatures)尽可能地hash到同一个bucket中,而不是不相似的两列。
由于列c和d要成为候选集,其signatures相似度至少为t。对signature矩阵,我们通过创建很大数目的hash函数(普通的hash函数,不是minhash函数)。对每个选择的hash函数,我们把列hash到buckets中,并将同一个bucket中的所有pairs作为候选pair。也就是说只要有一个hash函数将两列hash到同一个bucket中,它们就成为一个候选对,之后进行相似度计算。可以看出这样做同一个bucket中列两两之间才进行相似度计算,而不是所有列两两之间进行相似度计算,减少了计算量。
哈希函数数目和桶数目的协调:为了使每个bucket中的signatures数目相对较少,从而生成较少的候选pairs,我们需要调整hash函数和每个hash函数的buckets数目。但是也不能使用太多的buckets,否则真正相似的pairs都不会被任意一个hash函数wind up到同一个bucket中。
LSH的实现
1 首先将Signature Matrix分成一些bands,每个bands包含r行rows。b*r就是signatures的总长度(也就是在minhash阶段用于创建signatures的min hash函数的数目)。

2 然后把每个band哈希到一些bucket中(不同的band使用不同的hash函数,也就是对每个band我们都要创建一个hash函数)。使用不同hash函数同一个buckets数组?
这个方法的直觉含义就是,只要两个signatures在某个片断band上相似(hash到同一个bucket中),它们在整体上就有一定的概率相似,就要加入候选pairs进行比较!同一个bucket中的两列是局部相似的(因为只要某个band相似就会至少hash一次到同一个bucket中,这应该就是局部敏感哈希名称的来源),所以同一个bucket中的两两对都是候选对。如果两个signatures大部分都是相同的,那么存在bands 100%相同就有很大的机会。而两列如果不相似,即很少有相同的片段,那他们被hash到同一个bucket中的概率就相当小,只要bucket的数量要足够多,两个不一样的bands就会被哈希到不同的bucket中。There's a small chance that these segments of these columns are not identical, but they just happen to hash to the same bucket.We will generally neglect that probability as it can be made tiny,like 1 in 4 billion,if we use 2 to the 32nd power buckets.
Hash策略:This hash function hashes the values that a given column has in that band only.Ideally, we would make one bucket for each possible vector of b values that a column could have in that band.That is, we'd like to have so many buckets that the hash function is really the identity function, but that is probably too many buckets. 桶数目的计算的大小:For example, if b = 5 and the components of a signature are 32-bit integers,then they would be 2 ^ (5 * 32) or 2^160 of buckets.We can't even look at all these buckets to see what is in them at the end.So we'll probably want to pick a number of buckets that is smaller,say, a million or a billion.
也可以对所有bands使用一个hash函数,但是要对每个bands使用独立的桶数组,这样就算不同bands有相同的行也不会hash到同一个bucket中。而且这样lz觉得可能比上面的使用不同hash函数同一个buckets数组更好,不容易产生冲突。
bands大小和相似度阈值的选取准则
如果b很大(设置的bands很多),r很小,则会有很多pairs会分到同一个bucket中。也就是b很大时,更可能判定有相似性,这样我们应该设置相似性阈值相对低点。
相反,如果b设置的很小,r很大,这样就很难将两个signatures哈希到同一个bucket中,所以最好将相似性阈值设置高些。(相似性阈值是指原始文档中我们认为文档相似的阈值)
Note: lz这里并不说明b和r具体选取什么样的值,但是bucket的值越大越好,只要内存足够大就好。
LSH示例
可能比较的paris数目的计算:5,000,000,000个=(100,000 2),即100,000中选出两个,100,000*99999/2.
because of the randomness involved in minhashing, the columns C1 and C2 may agree in more or fewer than 80 of their rows but approximately.
LSH能保持文档相似性的示例
假设有两个document,它们对应的Signature Matrix矩阵的列分别为C1,C2,Signature Matrix还是分成20个bands,每个bands有5行。
假设C1、C2实际上有80%相似,则:
0.328是8成相似的两列C1、C2在某个band(一个band中有5个components)中完全一样的概率0.8^5,虽然很小,但计算得到C1、C2在20个bands中都不相似的概率为0.00035,几乎为0,也就是说20个bands中总有一个band检测到C1、C2是相似的,并且LSH检测他们相似的概率(hash到同一个bucket中的概率)相当大为0.99965。同时0.00035=1/3000,是false negative的概率。
假设C1、C2实际上有40%相似,则:
可以看出这时有20% false positives,but the false positive rate falls rapidly as the similarity of underlying sets decreases.For example, for 20% Jaccard similarity,we get less than 1% false positives.
假设C1、C2实际上有30%相似,则:
C1中的一个band与C2中的一个band完全一样的概率就是0.3^5=0.00243,那么C1与C2在20个bands中至少有一个一样的概率是1-(1-0.00243)^20=0.0474,换句话说就是,如果这两个document是30%相似的话,LSH中判定它们相似的概率是0.0474,也就是几乎不会认为它们相似。
LSH准确率分析
我们想要的LSH理想情况
设s是2个sets(docs、colums、signatures)真实相似度,t是相似度阈值,共享同一个bucket的概率为1时(也就是两列总是hash到同一bucket中,其应该推断出相似度是100%),那么两列的相似性越大,并且大于这个阈值t,说明两列是相似的(与应该推断出相似度是100%相符)。
理想阶跃函数:当两个sets相似度很高时(>t),总是分到同一个bucket中,相反相似度低时,总是不会分到同一个bucket中(分到同一bucket中的概率为0)。
实际情况:分析signature matrix的单行(两列)
阈值为t时的false pos和false neg。感觉图中false pos填充的区域不直观,反直觉,但是要记得false pos是相似性t小但是分到同一buckets中的概率。
由于两个minhash值相等的概率=underlying set的Jaccard相似度,所以单行对应的是图中对角线(红线)。
可知此时false比较多:That's not too bad.At least the probability goes in the right direction, but it does leave a lot of false positives and negatives.
False pos和neg的概率大小控制
这些false pos和false neg的概率是可以通过选取不同的band数量b以及每个band中的row的数量r来控制的。b和r都越大,也就是signatures的长度(signature矩阵的行数)越长,S曲线就越接近于阶跃函数,false positives and negatives相应就会减小,但是signatures越长,它们占用的空间的计算量就越大,minhash阶段就需要更多工作。通俗点就,就是在minhash阶段多弄几个minhash函数,就可以使LSH阶段的错误更小一些。
S曲线分析:阈值t的确定
直接在signature matrix中比较相似度不容易确定threshold t,而添加s,r后,可以根据理论很好的设置一个t=(1/b)^1/r,但是我们不管b和r的值是多少,怎么确定。
s是2个sets(docs、colums、signatures)真实相似度。则可得出以下概率计算公式:
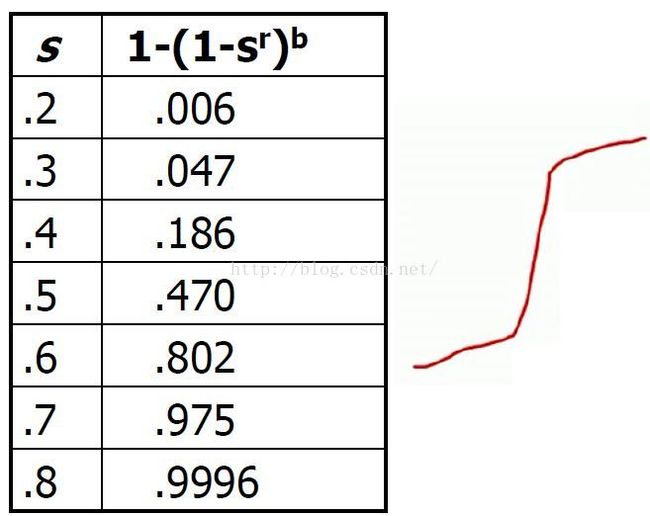
当b和r变大时,函数1-(1-s^r)^b (阈值s下相似的列hash到至少同一个桶中的概率)的增长类似一个阶跃函数step function。当阈值在大概(1/b)^1/r这个位置时跳跃。
这个阈值实际上是函数f(S) = (1-S^r)^b的不动点(近似值),也就是输入一个相似度S,得到一个相同的概率p(hash到同一个bucket中的概率)。当相似性相对不动点变大时,其hash到同一个bucket中的概率也变大,反之相似性相对不动点变小时,其hash到同一个bucket中的概率也变小了。Threshold t will be approximately (1/b)^1/r.But there are many suitable values of b and r for a given threshold. 所以应该选择t = (1/b)^1/r作为阈值,这样大于这个阈值说明两列相似,否则不相似。
除此之外,还可以通过AND和OR操作来控制,同样得到相同的S曲线。实际上上面的bands方法只是and-or操作的特例而已。[海量数据挖掘MMDS week7: 局部敏感哈希LSH(进阶)]
LSH分析实例
从上表中看出,0.4-0.6之间的跳跃最大,幅度超过0.6,thresh取值在这个范围内最优。实际计算(1/b)^1/r也正好在这个范围内。
LSH总结
[Locality Sensitive Hashing 详解]
皮皮blog
LSH的应用(LSH的三个变型)
应用一:entity resolution实体分辨(LSH变型1)
实体分辨会出现很多问题,例如通过人名合并人物可能的问题:people with the same name,so grouping by name will merge records for different people and worse, the same person may have their name written:middle initials,nickname - formal name,misspellings。
匹配消费者记录
Note:
1. We gave 100 points each for identical names, addresses, and phone numbers, so 300 was the top score.only 7,000 pairs of records received this top score, although we identified over 180 thousand pairs that were very likely the same person.Then we penalize differences in these three fields.Completely different names addresses or phones got zero score but small changes gave scores close to 100.
2. small spelling difference in the first names.the score for the name would be 90.If the last names were the same but the first name's completely different the score for the names would be 50.
3. how we set the threshold without knowing ground truth.That is, which pairs of records really were created by the same individuals.this is not a job you can do with machine learning, because there's no training set available.
Note:
1. we used exactly three hash functions.One had a bucket for each possible name.The second had a bucket for each possible address.And the third had a bucket for each possible phone number.Now, the candidate pairs were those placed in the same bucket by at least one of these hash functions.
2. finding those extra missed pairs would probably have cost more than they were worth to either company.
Names, address, phone怎么hash
How do we hash strings such as names so there is one bucket for each string?
第一种hash方法:现实中名字太多,可以不用hash,直接对names进行排序,相同名字的记录就连在一起了,这样之后再去score。How we hash to one bucket for each possible name since there are an infinite number of possible names.But we didn't really hash to buckets,rather we sorted the records by name and then the records with identical names appear consecutively in the list and we can score each pair with identical names.After that we resorted by address and did the same thing with records that had identical addresses.
第二种hash方法:Another option was to use a few million buckets, and deal with buckets that contain several different strings.follow the strategy we used when we did LSH for signatures we could hash say several million buckets and compare all pairs of records within one bucket.如果bucket的数目远远大于数据中实际出现的名字数目,发生冲突的概率是极小的。
结果确认Result validation: score多少分才算sure?
Note:
1. For the identical pairs, we looked at the creation dates at companies A and B.It turns out that there was a 10 day lag on average between the time the record was created by company A and the time that the same person went to company B to begin their service.
2. In order to reduce further the pairs of records we needed to score we only looked at pairs of records where the A record was created between 0 and 90 days before the B record, you'll get an average delay of 45 days.
3. 如果匹配池matches pool中的平均延迟时间lag time是10天(也就是所有都是validated)则有(45-10)/35=100%的是valid,反之,如果平均延迟时间lag time是45天(也就是所有的都超过45天的最长时限,都不是validated)则有(45-45)/35=0%的是valid。
什么数据field可以用于validation?
Any field not used in the LSH could have been used to validate, provided corresponding values were closer for true matches than false.
应用二:Minutiae:A New Way of Bucketing
(并不需要原始的LSH来创建buckets,更不用shingles和minhashing)
Fingerprint Matching指纹匹配
指纹表示
Note: minutiae: particular locations where something interesting happens to the ridges that form a fingerprint.Examples are where two ridges merge into one or where a ridge ends.So, the image of a fingerprint is replaced by a set of coordinates in the two dimensional space where minutiae are located.
指纹匹配中的LSH
通过方格(minutiaes)的集合来表示指纹
Note:
1. The grid must be scaled and orientated properly.
2. Since some minutiae will be right on or near a boundary, it is useful to regard such minutiae as present in the squares on both sides of the boundary.
3. 指纹匹配问题转化:we have reduced the problem of finding matching fingerprints to the problem of finding similar sets of grid squares that have minutiae.
指纹匹配的难点:矩阵是稠密的,Min-Hashing对稀疏矩阵更有效,否则可能分不开不同的指纹。The problem is that the resulting matrix is not sparse.The grid cannot be too fine or it will be unclear where minutiae belong.And as a result,the matrix's rows are the grid squares and its columns or the fingerprints sets will not be sparse.That means min hashing will not work very well.Each min hash will have relatively few different values, so we don't get a good distribution into a large number of buckets when we do the LSH.
Discretizing Minutiaes离散化Minutiaes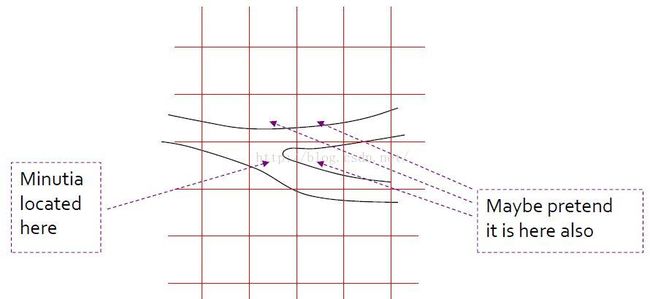
Note: 图中交叉点就是一个minutiaes,要加入到指纹表示中,同时其周围很近的方格也要加入到sets中。It appears the point of merger lies within this grid square.So, we add that square to the set representing the fingerprint.we might also want to add the squares that are very close to the exact point of merger, because in another image of the same fingerprint,the grid might be shifted slightly to the left or down.
LSH在指纹中的应用
表示成bit-vector
指纹候选对
Note:
1. 随机选出1024个集合,每个集合中有3个方格。For every LSH, if we pick some member of sets of grid squares or components of the bit-vectors that represent fingerprints.In our example, we'll use 1,024 sets of three grid squares each.For each set of three squares,we look at all the prints that have minutiae in each of these three squares.
2. 如果存在某个集合,两个指纹对应的3个方格都是1,那么这两个指纹就是候选对(要进一步比较是否相同)。
3. 选出的集合就像是LSH中的bucket。但是unlike a hash function, a fingerprint can be placed in many buckets.
LSH/Fingerprint示例
1. 每个指纹有20%的方格存在minutiaes,两个相同的指纹有80%的方格是agree的。The fact that we place minutiae in nearby squares if they are at the boundary helps make this assumption true.
2. if the fingerprints come from different fingers,then the probability that both prints are placed in this bucket(含3个squares的set) is really tiny.
3. 一个指纹在3个squares中有minutiaes的概率是(0.2)^3,两个指纹就是(0.2)^6.
相同指纹匹配成功概率分析
Note: And by using a larger number of sets of squares and perhaps four or five squares per set,we can reduce the false positive rate substantially while still keeping the false negative rate low.
应用三:A New Way of Shingling: Bucketing by Length
(LSH变型3:变型的shingling技术,实际上并没有使用MinHashing或者LSH)
寻找重复新闻文章
与文档相似度计算的不同点是:there is a special way of shingling that works well when the difference are mostly in the ads associated with the article.We shall also talk about a simple bucketing method that works when the number of sets is not too great.
minhashing + LSH方法实现
invented a form of shingling that is probably better than the standard approach we covered for those webpages that are of the type we just described.And they invented a simple substitute for LSH that worked adequately well for the scale of problem.They partitioned the pages into groups of similar length and they only compared pages in the same group or nearby groups.
minhashing + LSH运行更快更好:But they found that minhashing + LSH was better as long as the similarity threshold was less than 80%.
Note: 提高效率和减小错误的小tips: do the minhashing row by row,where you compute the hash value for each row number once and for all rather than once for each column.Remember that the rows correspond to the shingles and the columns to the web pages.
特殊的shingling技术
Note:
1. The key observation was to give more weight to the articles themselves than to the ads and other elements surrounding the article.That is, they did not want to identify as similar two articles from the same newspaper with the same ads and other elements, but different underlying stories.
2. buy sudzo是广告,i recommend ...是正文(包含较多stop words)。
3. 根据他们定义的shingle,正文变成shingles是:I recommend that, that you buy...
4. Notice that there are relatively few shingles and it does not guarantee that each word is part of even one shingle.
shingling变型的分析
The reason this notion of shingle makes sense is that it biases the set of shingles for a page in favor of the news article.文章中含有stop words,他们选用的是比较文章而不是广告,So these two pages have almost the same shingles, and therefore have very high Jaccard similarity.
皮皮blog
Review复习
Shingles
Note:2-shingles for ABRACADABRA : AB BR RA AC CA AD DA 7个
2-shingles for BRICABRAC : BR RI IC CA AB RA AC 7个
2-shingles in common : BR CA AB RA AC 5个
Jaccard similarity: 5/(7+7-5) = 5/9
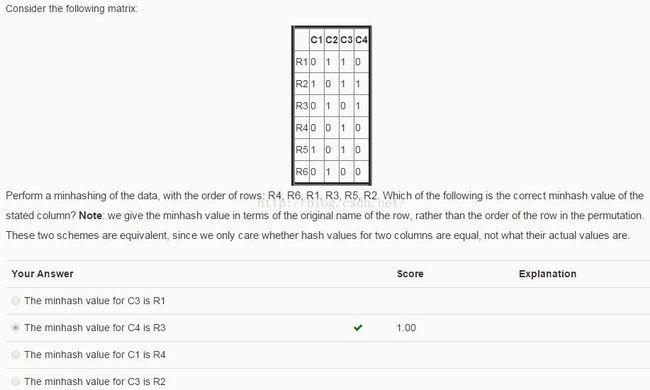
Min-Hashing
Note: R4得C3-R4;R6得C2-R6;R1过;R3得C4-R3;R5得C1-R5;R2过。
故:C1 C2 C3 C4
R5 R6 R4 R3
LSH
Note: band1中hash到同一bucket中的候选pairs是C1-C4, C2-C5
band2中hash到同一bucket中的候选pairs是C1-C6
band3中hash到同一bucket中的候选pairs是C1-C3, C4-C7
from:http://blog.csdn.net/pipisorry/article/details/48858661
ref: Mining Massive Datasets - week2: LSH的距离度量方法
海量数据挖掘MMDS week7: 局部敏感哈希LSH(进阶)