关联规则常用算法

  关联规则（Association Rules）是海量数据挖掘（Mining Massive Datasets，MMDs）非常经典的任务，其主要目标是试图从一系列事务集中挖掘出频繁项以及对应的关联规则。关联规则来自于一个家喻户晓的“啤酒与尿布”的故事，本文通过故事来引出关联规则的方法。

啤酒与尿布的故事
  在一家超市里，有一个有趣的现象：尿布和啤酒赫然摆在一起出售。但是这个奇怪的举措却使尿布和啤酒的销量双双增加了。这不是一个笑话，而是发生在美国沃尔玛连锁店超市的真实案例，并一直为商家所津津乐道。沃尔玛拥有世界上最大的数据仓库系统，为了能够准确了解顾客在其门店的购买习惯，沃尔玛对其顾客的购物行为进行购物篮分析，想知道顾客经常一起购买的商品有哪些。沃尔玛数据仓库里集中了其各门店的详细原始交易数据。在这些原始交易数据的基础上，沃尔玛利用数据挖掘方法对这些数据进行分析和挖掘。一个意外的发现是："跟尿布一起购买最多的商品竟是啤酒！经过大量实际调查和分析，揭示了一个隐藏在"尿布与啤酒"背后的美国人的一种行为模式：在美国，一些年轻的父亲下班后经常要到超市去买婴儿尿布，而他们中有30%～40%的人同时也为自己买一些啤酒。产生这一现象的原因是：美国的太太们常叮嘱她们的丈夫下班后为小孩买尿布，而丈夫们在买尿布后又随手带回了他们喜欢的啤酒。

  关联规则是一种大数据挖掘的任务，最初的动机是针对购物篮分析(Market Basket Analysis)问题提出的，例如上述的“啤酒与尿布”的故事，如果超市能够发现一些具有相关联的商品购物行为，通过对商品的适当调整可以提高顾客的购物体验，提升超市的销售额，因此如何发现这些潜在的规律呢？

本文首先介绍关联规则的任务，以及相关概念，其次介绍相关算法，目录索引如下：

1、关联规则形式化描述

  设$I=\{I_1,I_2,...,I_m\}$是一个项集（Item Set），$m$为项的个数，其中$I_i$表示第$i$个项，对应于一个个商品。事务（Transaction）$t_i$表示$I$的一个子集，对应于一个个订单。事务组成的集合记做$D=\{t_1,t_2,...,t_n\}$，通常也称作事务数据库。通常描述中，每一个事务都有唯一的编号，记做TID，每个事务中都包含若干个项Items。
  关联规则是形如$X\to Y$的蕴涵式，其中， $X$和$Y$分别称为关联规则的先导(antecedent或left-hand-side, LHS)和后继(consequent或right-hand-side, RHS) 。其中，关联规则$XY$，存在支持度和置信度，定义如下：

• 支持度（$X\to Y$）$=\frac{同时包含X和Y的事务数量}{所有事务数量}$，理解为某一个项出现的概率。通常设置一个阈值minsupport，当支持度不小于该值时认为是频繁项；
• 置信度（$X\to Y$）$=\frac{同时包含X和Y的事务数量}{包含X的事务数量}$，理解为在X事务的基础上，X和Y均出现的条件概率。

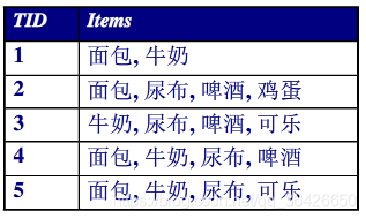
例题1：分别计算3-项集“面包，牛奶，尿布”和“面包→牛奶，尿布”对应支持度和置信度。

1.可统计“面包，牛奶，尿布”同时出现的TID有4和5，所以支持度是2/5；
2.面包出现的TID有1,2,4,5，因此支持度为2/4。

因此关联规则实际上包含两个子任务：

• 频繁模式发现：也称频繁模式挖掘、频繁项挖掘等，是指从一系列候选的项中选择频繁的部分，通常衡量频繁的程度可以是对每一项出现的频率，当超过某一阈值是则任务这个项是频繁的。
• 生成关联规则：在已经发现的最大频繁项目集中，寻找置信度不小于用户给定的minconfidence的关联规则。

2、Apriori算法

  Apriori算法是经典的关联规则算法，其主要思路如下图所示：

算法流程：

1. 首先对数据库中进行一次扫描，统计每一个项出现的次数，形成候选1-项集；
2. 根据minsupport阈值筛选出频繁1-项集；
3. 将频繁1-项集进行组合，形成候选2-项集；
4. 对数据库进行第二次扫描，为每个候选2-项集进行计数，并筛选出频繁2-项集；
5. 重复上述流程，直到候选项集为空；
6. 根据生成的频繁项集，通过计算相应的置信度来生成管理规则。

  其中如果项集中包含k个不同的项，称之为k-项集。候选k-项集记做$C_k$，频繁k-项集记做$L_k$。

  频繁模式挖掘的基本前提是：

• 如果一个集合是频繁项集，则它的所有子集都是频繁项集。
• 如果一个集合不是频繁项集，则它的所有超集都不是频繁项集。

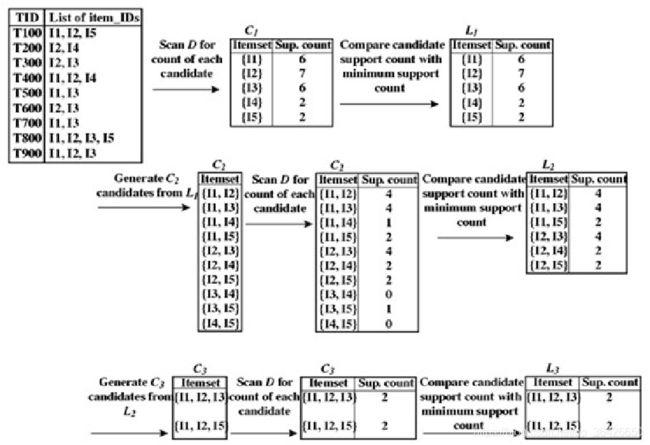
例题2：使用Apriori算法对事务集$D$进行频繁项挖掘，其中minsupport.count=2.

  首先对事务数据库$D$进行扫描，统计各个1-项的计数。由于最小计数阈值minsupport.count=2，因此可以筛选出频繁1-项集“$l_1,l_2,l_3,l_4,l_5$”。其次两两组合，形成$5\times 4÷2=10$个候选2-项集$C_2$，并进行第二次扫描数据库进行计数，发现$(l_1,l_4),(l_3,l_4),(l_3,l_5),(l_4,l_5)$低于阈值，所以剔除掉。对剩余的频繁2-项集$L_2$进行两两组合，去除重复的组合后形成候选3-项集$C_3$，以此类推，最终得到频繁3-项集为$(l_1,l_2,l_3),(l_1,l_2,l_5)$。

Apriori算法的特点：

• 简单且易于实现，是最具代表性的关联规则挖掘算法
• 随着数据集规模的不断增长，逐渐显现出一定的局限性：
    （1）需多次扫描数据库，很大的I/O负载，算法的执行效率较低；
    （2）产生大量的候选项目集，尤其是候选2-项集占用内存非常大，会消耗大量的内存；
    （3）对于每一趟扫描，只有当内存大小足够容纳需要进行计数的候选集时才能正确执行。如果内存不够大，要么使用一种空间复杂度更小的算法，要么只能对一个候选集进行多次扫描，否则将会出现“内存抖动”的情况，即在一趟扫描中页面频繁地移进移出内存（页面置换算法也无法避免内存抖动问题），造成运行时间的剧增。

3、PCY算法

  为了改进Apriori算法，PCY由Park，Chen和Yu等提出，其目标是为了降低Apriori算法频繁的扫描数据库，其次降低候选项集所占用的内存。其主要创新点有：

• 将哈希函数应用到频繁项挖掘中；
• 第一次扫描事务数据库时，将剩余的空间存放哈希表，从而降低第二次扫描时占用的大量空间。

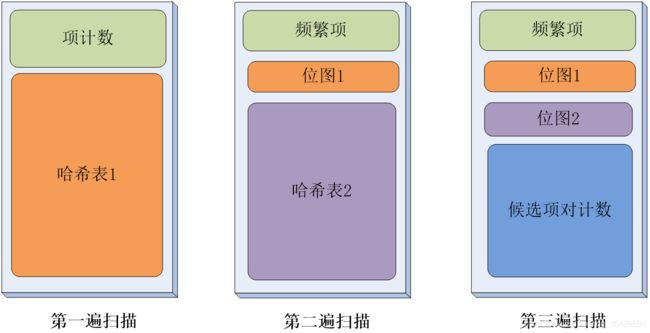
  如上图，左边两个图表示Apriori算法的前两次扫描过程，可知第一次扫描内存空闲很大，而第二次扫描占用空间很多；右侧两个图则表示PCY算法的两次扫描，第一次扫描除了对1-项集进行计数外，额外利用一个2-项哈希表存储每个2-项的计数，再第二次扫描时则利用该哈希表对应的位图来判断是否保留该2-项，从而减少候选2-项集大小。

  PCY主要思想可总结如下：

1. 首先第一次扫描事务数据库$D$，并对候选1-项集$C_1$进行计数，根据阈值筛选出频繁1-项集$L_1$；
2. 在第一次扫描的同时，对事务集中每个事务中各个项进行两两组合，并通过哈希函数映射到相应的桶中，并将相应的桶计数+1；
3. 第二次扫描之前，首先根据每个桶中的计数来判断是否为频繁桶，频繁桶是指计数不低于某个阈值的桶。频繁的桶对应的位图记做1，否则记做0；
4. 第二次扫描事务数据库，此时根据频繁1-项集$L_1$生成一系列的2-项组合，分别通过哈希函数获得其桶的编号，并根据位图来判断。如果对应的位图值为1，则将其保留，否则剔除。因此最后保留的就是候选2-项集$C_2$，对其进行计数并筛选频繁2-项集$L_2$

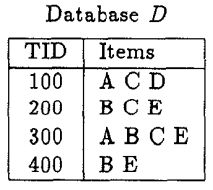
例题3：使用PCY算法生成频繁2-项集，其中minsupport.count=2，哈希函数为：

事务及集合$D$：

1.首先对1-项集进行计数，筛选出频繁1-项集$L_1$为{A}，{B}，{C}，{E}；
2.其次根据事务集中每个事务的项两两组合，并通过哈希函数映射到7个桶中。例如$\{A,C\}$哈希值为$(1\times 10+3)mod7=6$，所以其映射到下标为6的桶中；最终形成的桶如下图所示，如果桶的计数超过不小于2，则为频繁桶，位图对应为1。所有桶的计数分别为3,1,2,0,3,1,3，位图对应为1,0,1,0,1,0,1。
3.频繁1-项集$L_1$，中两两组合，并将每一个组合通过哈希函数得到对应的桶编号，如果对于的位图为1，则保留为候选2-项。最终从6个项中筛选出$\{A,C\},\{B,C\},\{B,E\},\{C,E\}$共4个作为候选项集$C_2$；
4.最后第二次扫描计数，得到对应的频繁2-项集$L_2$为$\{A,C\},\{B,C\},\{B,E\},\{C,E\}$

  因此总的来说，PCY算法的关键在于在第一次和第二次扫描之间通过哈希计数提前过滤掉一部分2-项集，使得候选2-项集规模变小，而这种筛选的规则则是根据频繁桶来确定。

PCY算法特点：

• 优点
    高效地产生频繁项集，提升了性能
    减少了数据库的扫描次数
    减少计数所需的内存空间的大小
• 分析
    最差的情况：所有桶都是频繁桶，则第二遍扫描中PCY算法需要计算的相对数目与Apriori算法相比没有任何减少
    在寻找频繁3-项集以及更多项集时，PCY算法与Apriori算法相同
    如果桶的个数越多，每个桶内分的项数量变少
    如果不频繁的项映射到频繁的桶中，则可能不易过滤（改进：多阶段算法）

4、多阶段算法

  事实上，PCY算法面临一个问题，即由于哈希函数的原因，有些非频繁项被映射到了频繁桶中，导致这部分非频繁项很难被过滤掉，因此多阶段算法旨在解决这个问题。其主要思路是：

1. 在PCY的第一遍和第二遍之间插入额外的扫描过程，将2-项集哈希到另外的独立的哈希表中（使用不同的哈希函数）
2. 在每个中间过程中，只需哈希那些在以往扫描中哈希到频繁桶的频繁项。

如图所示：

1. 首先进行第一次扫描。该扫描与PCY第一次扫描一样，首先对1-项集计数，并将每个事务中各个项两两组合，通过第一个哈希函数映射到哈希表1中；
2. 在第二次扫描时，使用第二个哈希表。当2-项集$\{i,j\}$同时满足
   （1）$i,j$均为频繁项、（2）$\{i,j\}$在第一个哈希表中映射到频繁桶中；
   时，该2-项集可以映射到第二个哈希表中；
3. 在第三次扫描时，根据频繁1-项集中各项两两组合，对于每个2-项集，当前仅当同时满足：
   （1）$i,j$均为频繁项、（2）$\{i,j\}$在第一个哈希表中映射到频繁桶中、（3）$\{i,j\}$在第二个哈希表中映射到频繁桶中；
   时，才保留其作为候选2-项集$C_2$。
4. 对所有候选2-项集筛选出频繁2-项集$L_2$

多阶段算法特点：

1. 因为在第二趟扫描时，不是所有的2-项集都被散列到桶中，因此桶的计数值变得比第一趟扫描时更小，最终结果是更多的桶变成非频繁桶；
2. 由于两次扫描采用的哈希函数不同，那些在第一趟扫描时被散列到频繁桶中的非频繁2-项集很可能在第二趟扫描时被哈希到一个非频繁桶中
3. 多阶段算法寻找频繁2-项集不只局限于使用3次扫描

5、多哈希算法

  多哈希算法与PCY算法基本一致，不同在于PCY算法只使用一个哈希表，而多哈希算法则是使用了多个哈希表，其算法思想与PCY一致，只是在判断是否是候选2-项集时，需要同时判断多个对应位图是否均为1，如下图所示：

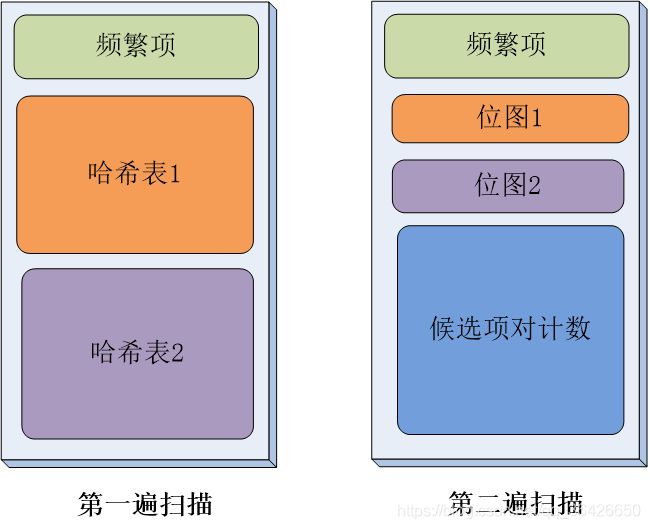
多哈希算法特点：

1. 只要桶的平均计数不小于阈值，频繁桶的数目仍然比较多，这样一个非频繁2-项集同时哈希到两个哈希表的频繁桶内的概率就更低，可以减少第二遍扫描的运算量
2. 风险：
     使用两个哈希表时，每个哈希表仅有PCY算法的一半的桶，这样每个桶上的平均计数会翻倍，必须保证大多数桶的计数不会达到阈值
     桶的平均计数可能会超过阈值
3. 多哈希算法也不只局限于使用两个哈希表：

6、FP-Tree算法

  先前的方法均存在一个问题，即频繁的对数据库进行扫描，而每次扫描的目的则是为了计数，因此如何只对数据库进行两次扫描便可以对所有可能的频繁项进行计数呢？FP-Tree算法巧妙的解决了这个问题。
  FP-Tree算法主要分为两个步骤：构建FP树和频繁模式挖掘。

一、构建FP树算法：

1. 对事务数据库$D$进行一次扫描，统计所有项的计数，并根据最小支持度阈值保留频繁1-项集；
2. 对频繁1-项集中所有的项递减顺序排列，形成对应的Head Table，其中Head Table每个元素表示频繁1-项集及其计数，指针默认为空；
3. 创建一个根结点，扫描第二遍事务数据库$D$，每一个事务对应的所有排序的项依次插入树中，计数默认为1，如果已存在该节点，则计数+1（同一个项在每个事务记录内排号相同时，此时两个结点是同一个，则直接+1）。若相同的项不在同一个分支时，通过指针相连。

二、频繁模式挖掘

1. 根据Head Table自底向上顺序依次进行频繁项挖掘，此时对于的元素作为条件模式基；
2. 在FP树中寻找相应的路径，且计数取最小值，去除掉小于阈值的项，保留不小于阈值的项；
3. 根据条件模式基获得相同基的频繁项。

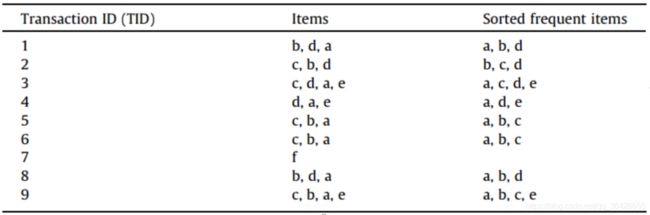
例题4：已知最小支持度阈值为3，使用FP-Tree算法进行频繁项挖掘，事务数据库如图所示：

  如图可知，事务数据库中共有9个事务，6个项。此时可知a,b,c,d,e,f的计数分别为7,6,5,5,3,1。首先第一次扫描后可过滤掉“f”，其次根据各自计数在每个事务记录内降序排列。
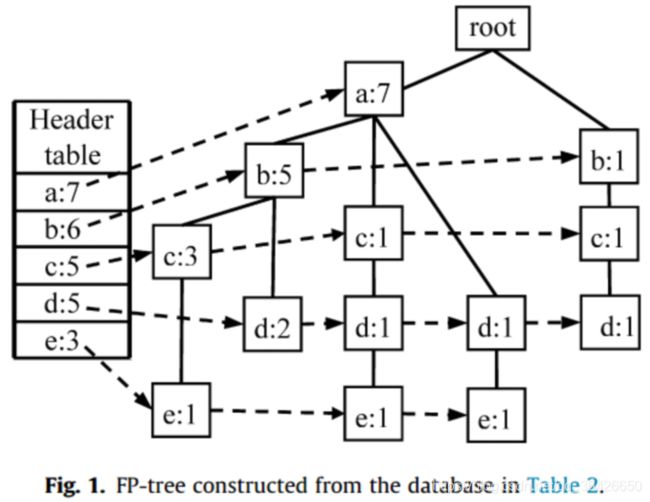
  根据计数生成Head Table；
  其次构建FP树，例如事务记录TID=1开始，向根结点依次插入结点(a:1)，(b:1)，(d:1)，此时Head Table中的a,b,d指针分别指向新增的结点。当TID=2时，从根结点插入(b:1)，(c:1)，(d:1)，需要注意的是，虽然当前也插入了b和c，但由于其层数与TID1不同，所以是在新的分支上。而对于TID=3时，第一个项是a，所以直接在(a:1)上计数，变为(a:2)。
  以此类推，即可生成如下图所示的FP-树：
  其次进行频繁项挖掘，先以e开始，可知所有路径以e结尾的有(a:7,b:5,c:3,e:1)、(a:7,c:1,d:1,e:1)，(a:7,d:1,e:1)。根据条件模式基，需要将每个结点的计数变为最小的值，即变为(a:1,b:1,c:1,e:1)、(a:1,c:1,d:1,e:1)，(a:1,d:1,e:1)。此时可以发现每个项的计数有(a:3)，(b:1)，(c:2)，(d:2)，(e:3)，由于阈值为3，则只保留(a:3)和(e:3)。因此可以得到频繁项有(ae:3)和(e:3)。需要注意的是，当前的基底是e，因此必须包含e，例如(a:3)不是e的条件模式基，则不能包含该项。

FP-Tree算法特点：

1. FP-Tree算法只需要进行两次扫描即可完成频繁模式挖掘，大大减少了I/O开销；
2. 通过Head Table可对相同的项进行计数，省去了重复计数的时间开销，计数完全可以在内存内外存。

7、XFP-Tree算法

  FP-Tree算法有许多可改进之处，例如如果当事务的数量非常庞大时，构建FP树会占用大量的时间，XFP-Tree算法旨在并行的构建FP树来提升效率。

  XFP-Tree算法需要创建两个数据结构，分别是XFP-Tree和位图矢量：

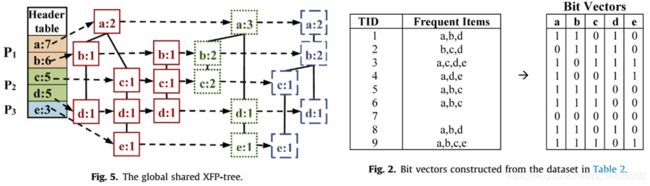
1. XFP树：与FP树构建方式相同，不同点在于使用多核机制。首先对Head Table进行划分，划分的数量与内核数成整数倍，划分时尽量保证相对平均；其次在不同的分区上用不同的CPU核创建FP树，该过程是并行执行的，如下图所示（例4的示例），3个CPU核并行构建，每个颜色代表不同的CPU核，不同核构建的FP树通过指针连接。
   
2. 位图矢量：按照项对每个事务进行记录，例如TID1的事务只有abd三个项，所以位图为1，其他为0，即11010。位图矢量的功能是用于对项进行计数，而计数也可以通过多核机制进行并行。例如项ab，cd和e分别分配给P1，P2和P3执行计数。

8、GPApriori算法

  有相关工作对Apriori进行了改进，除了先前介绍的PCY，多阶段、多哈希外，使用GPU进行频繁模式挖掘也是一种改进之处。 GPApriori算法则使用GPU进行频繁项挖掘。

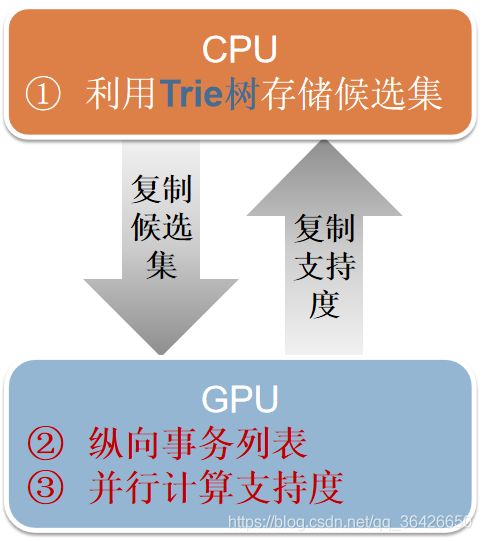
  GPApriori算法主要创新点为：（1）使用字典树来保存候选项，（2）使用纵向事务列表，（3）可并行实现支持度计算；

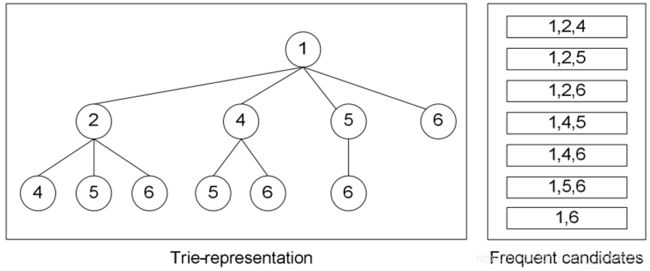
一、字典树
  由于许多的候选项可能有相同的前缀，例如候选3-项“1,2,4”和“1,2,5”都有相同的前缀“1,2”，因此可以使用字典树保存。

二、事务的纵向表示

  存储一个对应于每个候选集的事务id列表（tidset），每个列表也可以被表示为一个位掩码（bitset）。例如下图，左侧为传统的事务表示，右侧为纵向表示，Candidate表示候选的项集，tidset则表示对应项集包含的事务记录，其可以使用bit码表示。例如1-项集只有第1和第4个事务存在，所以bit码可以写成1001。
  之所以可以使用纵向表示，是因为：
（1）当判断两个项的组合是否是频繁项时，直接将二者对应的bit码按位求与计算，结果中1的个数即为支持度计数值。例如判断2-项集(1,3)的计数，则直接求1001和1111的按位与，结果为1001，则说明有两个事务满足这个20项集，再例如3-项集(1,3,5)，则可以表示为(1,3)的1001和(5) 的1101按位与，结果为1001，说明也有两个事务同时包含项1、3、5。
（2）使用纵向表示法，可以并行的对支持度进行计数，这也是第三个贡献。

三、并行支持度计算
  当使用纵向表示时，可以将纵向事务表划分为多个分块，每个分块置于GPU计算节点上，最后使用并行归约法获得总计数。

参考文献
【4】Zhang F, Zhang Y, Bakos J. Gpapriori: Gpu-accelerated frequent itemset mining[C]//Cluster Computing (CLUSTER), 2011 IEEE International Conference on. IEEE, 2011: 590-594.

---

  博客记录着学习的脚步，分享着最新的技术，非常感谢您的阅读，本博客将不断进行更新，希望能够给您在技术上带来帮助。