CS224D 课程学习笔记 L05
Lecture 5. Neural Networks
这节课我们将要学习神经网络。教授本节课slides是按照单层神经网络的前向计算、损失函数、后向计算,两层神经网络的前向计算,损失函数,后向计算两个方面来讲解以及推导梯度公式。notes III是按照神经元、单层神经网络、最大间隔目标函数、元素级别的后向传播训练、向量级别的后向传播训练这些神经网络的基础来讲解。因为本章的Back Propagation是神经网络最最最重要和艰难的知识点,所以我的本次笔记会包含slides和notes的每个知识点,务必把BP研究明白!
首先,先从Notes III里讲解的神经网络的基础知识着手,然后结合课上的单层神经网络和两层神经网络的计算。
文章目录
- Lecture 5. Neural Networks
- 神经网络的基础(Notes III)
- 1. 神经元
- 2.神经网络的某一层
- 3. 前向计算
- 4. 最大间隔目标函数
- 5. 后向传播训练--元素级别
- 6. 后向传播训练--向量级别
- 单层神经网络(slides)
- 两层神经网络(slides)
神经网络的基础(Notes III)
在前面的课堂上我们了解了建立非线性分类器的必要性,因为现实中的大部分数据都不是线性可分的。接下来我们从几个方面来学习神经网络:
1. 神经元
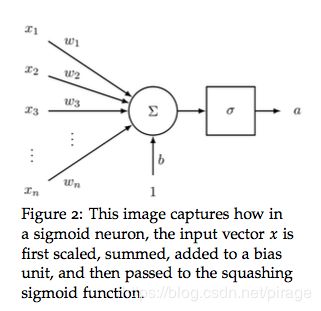
神经元就是一个 n n n 个输入产生一个输出的计算单元。不同的神经元通过它们的参数(也叫做权重)生成不同的输出。sigmoid或者叫二元逻辑回归单元是一种比较流行的神经元,它能够输入 n维向量 x x x生成一个标量激活值 a a a,同时它还有一个 n维权重向量 w w w 以及偏置标量 b b b。sigmoid神经元的输出为:
a = 1 1 + e x p ( − ( w T x + b ) ) = 1 1 + e x p ( − ( [ w t b ] ⋅ [ x 1 ] ) ) a = \frac{1}{1 + exp(-(w^Tx+b))} = \frac{1}{1 + exp(-([w^t\ \ b]\cdot[x\ \ 1]))} a=1+exp(−(wTx+b))1=1+exp(−([wt b]⋅[x 1]))1
sigmoid神经元的可视化如下图:
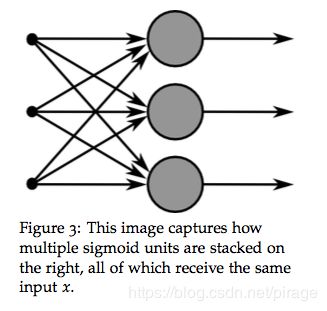
2.神经网络的某一层
我们将神经元扩展一下,考虑这种情况:当输入向量 x x x 被送入到多个单个的神经元中,那么这就构成了神经网络中的一层。如下图所示:
假设不同神经元的权重为 { w ( 1 ) , … , w ( m ) } \{w^{(1)},…,w^{(m)}\} {w(1),…,w(m)}, 偏置为 { b 1 , … , b m } \{b_1,…,b_m\} {b1,…,bm}, 各自的激活值为 { a 1 , … , a m } \{a_1,…,a_m\} {a1,…,am},则:
a 1 = 1 1 + e x p ( w ( 1 ) T x + b 1 ) a_1 = \frac{1}{1+exp(w^{(1)T}x+b_1)} a1=1+exp(w(1)Tx+b1)1
…
a m = 1 1 + e x p ( w ( m ) T x + b m ) a_m = \frac{1}{1+ exp(w^{(m)T}x + b_m)} am=1+exp(w(m)Tx+bm)1
我们定义一些简写用来简化,同时对后续复杂的网络也很有帮助:
σ ( z ) = [ 1 1 + e x p ( z 1 ) ⋮ 1 1 + e x p ( z m ) ] \sigma(z) = \begin{bmatrix}{\frac{1}{1+exp(z_1)}}\\\vdots\\{\frac{1}{1+exp(z_m)}}\\\end{bmatrix} σ(z)=⎣⎢⎡1+exp(z1)1⋮1+exp(zm)1⎦⎥⎤
b = [ b 1 ⋮ b m ] ∈ R m b = \begin{bmatrix}b_1\\\vdots\\b_m\end{bmatrix} \in R^m b=⎣⎢⎡b1⋮bm⎦⎥⎤∈Rm
W = [ − w ( 1 ) T − … − w ( m ) T − ] ∈ R m ∗ n W = \begin{bmatrix}-\ w^{(1)T}\ -\\\dots\\-\ w^{(m)T}\ -\end{bmatrix} \in R^{m*n} W=⎣⎡− w(1)T −…− w(m)T −⎦⎤∈Rm∗n
然后,我们可以得到变换后的输出为: z = W x + b z = Wx + b z=Wx+b
则,sigmoid函数的激活值就是:
a = [ a ( 1 ) ⋮ a ( m ) ] = σ ( z ) = σ ( W x + b ) a = \begin{bmatrix}a^{(1)}\\\vdots\\a^{(m)}\end{bmatrix} = \sigma(z) = \sigma(Wx+b) a=⎣⎢⎡a(1)⋮a(m)⎦⎥⎤=σ(z)=σ(Wx+b)
这些激活值代表了什么呢?这些值可以看成是数据的特征结合权重后的表现的指标,然后我们就可以用这些激活值来完成分类任务。
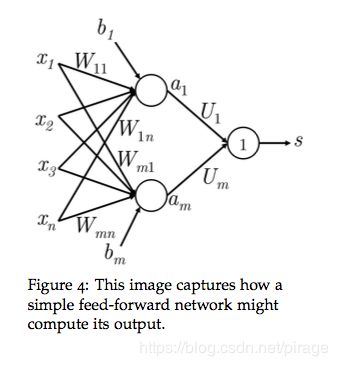
3. 前向计算
到目前为止我们了解了单层sigmoid神经元输入 x ∈ R n x\in R^n x∈Rn 后是如何创建激活值 a ∈ R m a \in R^m a∈Rm的,但是这样做的直观意义是什么?我们以NLP中的实体命名识别任务为例,假设句子:
“Museums in Paris are amazing.”
我们想要对中心词“Paris”是否是命名实体进行分类。在这种情况下,我们可能不会需要掌握窗口中词的词向量的意义,而是想要根据窗口中的词的顺序来分类。例如,“Museums”作为句首的词,只有紧接着的第二个词是“in”的时候才重要。这种非线性决策边界通常不是把输入直接传递到softmax中就可以得到,而是需要通过上一小节中的中间层网络的得分才能得到。
我们定义一个矩阵 U ∈ R m ∗ 1 U \in R^{m*1} U∈Rm∗1 ,作用于激活值 a a a , 得到非规范化的得分,用来完成分类:
s = U T a = U T f ( W x + b ) s=U^Ta = U^Tf(Wx+b) s=UTa=UTf(Wx+b)
f f f 表示激活函数。
维度分析:假设我们定义词向量的维度为 4 维,输入的窗口大小为 5 ,那么输入向量 x x x 的维度为20 , x ∈ R 20 x\in{R^{20}} x∈R20。假设我们在隐藏层使用 8 个sigmoid单元,然后激活后生成一个输出得分, 则有 W ∈ R 8 ∗ 20 W\in{R^{8*20}} W∈R8∗20, b ∈ R 8 b \in {R^8} b∈R8, U ∈ R 8 ∗ 1 U \in {R^{8*1}} U∈R8∗1, s ∈ R s \in {R} s∈R。
前向传播计算的过程为:
z = W x + b z = Wx + b z=Wx+b
a = σ ( z ) a = \sigma(z) a=σ(z)
s = U T a s = U^Ta s=UTa
前向过程网络可视化如下图:
4. 最大间隔目标函数
和其他机器学习算法一样,神经网络也需要目标函数,通过最大化或者最小化目标函数度量产生的有益点或者误差。这一小节,我们来讨论一个流行的误差矩阵,叫做最大间隔目标,它的原理是保证分类正确的数据的得分,比分类错误的数据的得分高。
沿用上小节的例子,我们将正确的窗口“Museums in Paris are amazing”的得分标记为 s s s , 将错误的窗口"Not all museums is Paris"的得分标记为 s c s_c sc。那么,我们的目标函数就是最大化 ( s − s c ) (s-s_c) (s−sc) 或者最小化 ( s c − s ) (s_c - s) (sc−s)。
我们调整目标函数,保证只有当 ( s c ) > s = > ( s c − s ) > 0 (s_c) > s => (s_c - s)>0 (sc)>s=>(sc−s)>0时,才计算误差。这样调整的原因是:我们只关心比错误数据得分更高的正确数据,其他的不重要。也就是,当 s c > s s_c > s sc>s时误差为 ( s c − s ) (s_c - s) (sc−s),否则误差为0。所以,优化目标就调整为:
最小化 J = m a x ( s c − s , 0 ) J = max(s_c -s, 0) J=max(sc−s,0)
然而,上式并不能创造一个安全的间隔,从这个意义上说,这个目标函数是由风险的。我们期望正确类别数据的得分比错误类别数据的得分能高出一个间隔 Δ \Delta Δ,换句话说,我们期望当 ( s − s c < Δ ) (s-s_c < \Delta) (s−sc<Δ) 时计算误差,而不是 ( s − s c < 0 ) (s - s_c < 0) (s−sc<0)时计算。优化函数又调整为:
最小化 J = m a x ( 0 , Δ + s c − s ) J = max(0, \Delta + s_c - s) J=max(0,Δ+sc−s)
我们通过设置 Δ = 1 \Delta = 1 Δ=1来规范化间隔。
如果想要了解更多关于最大间隔的信息,可以查阅SVM算法中经常会出现的功能和几何间隔。
最终,我们定义所有训练窗口的优化函数为:
最小化 J = m a x ( 0 , 1 + s c − s ) J = max(0, 1+s_c-s) J=max(0,1+sc−s)
上式中, s c = U T f ( W x c + b ) s_c = U^Tf(Wx_c+b) sc=UTf(Wxc+b), s = U T f ( W x + b ) s = U^Tf(Wx+b) s=UTf(Wx+b)。
5. 后向传播训练–元素级别
这一小节是本节课最重要的部分,也是这门课程最难的部分!
接下来我们讨论下第4小节得到的损失函数,在 J > 0 J>0 J>0 的时候如何对各个变量进行训练, J = 0 J = 0 J=0时说明得到的预测时正确的,不需要更新。我们还是选择使用梯度下降(或其变种SGD)来更新梯度,所以依旧需要每个参数的梯度信息。
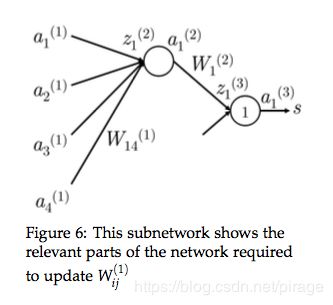
后向传播是一种允许使用链式法则来分化计算每个参数的损失梯度的手段,下图可以帮助我们进一步了解后向传播:
上图是一个单隐层和单输出的神经网络,第 k k k 层的第 j j j 个神经元接收输入 z j ( k ) z_j^{(k)} zj(k) ,激活产生输出 a j ( k ) a_j^{(k)} aj(k)。我们也对其他变量做一些标记,便于后续公式推导:
- x i x_i xi 是神经网络的输入。
- s s s 是神经网络的输出,是一个标量。
- 每个层(包括输入层和输出层)都有接收输入和产生输出的神经元,第 k k k 层的第 j j j 个神经元接收输入 z j ( k ) z_j^{(k)} zj(k) ,激活产生输出 a j ( k ) a_j^{(k)} aj(k)。
- 将 z j ( k ) z_j^{(k)} zj(k) 处的累积传播误差记为 δ j ( k ) \delta_j^{(k)} δj(k)。
- 第1层是指输入层,而不是第一个隐含层,输入层的 x j = z j ( 1 ) = a j ( 1 ) x_j = z_j^{(1)} = a_j^{(1)} xj=zj(1)=aj(1)。
- W ( k ) W^{(k)} W(k) 是转移矩阵,将第 k k k 层的输出映射到第 k + 1 k+1 k+1 层的输入。第3小节中的 W ( 1 ) W^{(1)} W(1) 和 W ( 2 ) W^{(2)} W(2) 分别表示 W W W和 U U U。
开始推导:假设损失 J = ( 1 + s c − s ) J = (1+s_c - s) J=(1+sc−s)为正,我们想要更新参数 W 14 ( 1 ) W_{14}^{(1)} W14(1),我们要记住的一点, W 14 ( 1 ) W_{14}^{(1)} W14(1)只对 z 1 ( 2 ) z_1^{(2)} z1(2)和 a 1 ( 2 ) a_1^{(2)} a1(2)有贡献。只有它们贡献过的值才对后向传播梯度有影响,明白这点很重要!下图可以帮助我们理解接下来的求导过程:
对参数 W i j ( 1 ) W_{ij}^{(1)} Wij(1)求梯度:
回顾一下前向计算的公式:
z = W ( 1 ) x + b z = W^{(1)}x +b z=W(1)x+b a = σ ( z ) = f ( z ) a = \sigma(z) = f(z) a=σ(z)=f(z) s = W ( 2 ) a s = W^{(2)}a s=W(2)a
目标是求 ∂ J ∂ W i j ( 1 ) \frac{\partial{J}}{\partial{W_{ij}^{(1)}}} ∂Wij(1)∂J,首先由最大间隔损失可以得到: ∂ J ∂ s = − ∂ J ∂ s c = − 1 \frac{\partial{J}}{\partial{s}} = -\frac{\partial{J}}{\partial{s_c}} = -1 ∂s∂J=−∂sc∂J=−1,所以简单起见,我们计算 ∂ s ∂ W i j ( 1 ) \frac{\partial{s}}{\partial{W_{ij}^{(1)}}} ∂Wij(1)∂s:
∂ s ∂ W i j ( 1 ) = ∂ W ( 2 ) a ( 2 ) ∂ W i j ( 1 ) = ∂ W i ( 2 ) a i ( 2 ) ∂ W i j ( 1 ) = W i ( 2 ) ∂ a i ( 2 ) ∂ W i j ( 1 ) \frac{\partial{s}}{\partial{W_{ij}^{(1)}}} = \frac{\partial{W^{(2)}a^{(2)}}}{\partial{W_{ij}^{(1)}}} = \frac{\partial{W_i^{(2)}a_i^{(2)}}}{\partial{W_{ij}^{(1)}}} = W_i^{(2)} \frac{\partial{a_i^{(2)}}}{\partial{W_{ij}^{(1)}}} ∂Wij(1)∂s=∂Wij(1)∂W(2)a(2)=∂Wij(1)∂Wi(2)ai(2)=Wi(2)∂Wij(1)∂ai(2)
= W i ( 2 ) ∂ a i ( 2 ) ∂ z i ( 2 ) ∂ z i ( 2 ) ∂ W i j ( 1 ) = W_i^{(2)} \frac{\partial{a_i^{(2)}}}{\partial{z_i^{(2)}}}\frac{\partial{z_i^{(2)}}}{\partial{W_{ij}^{(1)}}} =Wi(2)∂zi(2)∂ai(2)∂Wij(1)∂zi(2)
= W i ( 2 ) f ′ ( z i ( 2 ) ) ∂ z i ( 2 ) ∂ W i j ( 1 ) = W_i^{(2)} f\prime(z_i^{(2)}) \frac{\partial{z_i^{(2)}}}{\partial{W_{ij}^{(1)}}} =Wi(2)f′(zi(2))∂Wij(1)∂zi(2)
= W i ( 2 ) f ′ ( z i ( 2 ) ) ∂ ∂ W i j ( 1 ) ( b i ( 1 ) + a 1 ( 1 ) W i 1 ( 1 ) + a 2 ( 1 ) W i 2 ( 1 ) + a 3 ( 1 ) W i 3 ( 1 ) + a 4 ( 1 ) W i 4 ( 1 ) ) = W_i^{(2)} f\prime(z_i^{(2)}) \frac{\partial}{\partial{W_{ij}^{(1)}}}(b_i^{(1)} +a_1^{(1)}W_{i1}^{(1)} +a_2^{(1)}W_{i2}^{(1)}+a_3^{(1)}W_{i3}^{(1)}+a_4^{(1)}W_{i4}^{(1)} ) =Wi(2)f′(zi(2))∂Wij(1)∂(bi(1)+a1(1)Wi1(1)+a2(1)Wi2(1)+a3(1)Wi3(1)+a4(1)Wi4(1))
= W i ( 2 ) f ′ ( z i ( 2 ) ) ∂ ∂ W i j ( 1 ) ( b i ( 1 ) + ∑ k a k ( 1 ) W i k ( 1 ) ) = W_i^{(2)} f\prime(z_i^{(2)})\frac{\partial}{\partial{W_{ij}^{(1)}}}(b_i^{(1)} + \sum_ka_k^{(1)}W_{ik}^{(1)}) =Wi(2)f′(zi(2))∂Wij(1)∂(bi(1)+k∑ak(1)Wik(1))
= W i ( 2 ) f ′ ( z i ( 2 ) ) a j ( 1 ) ( 只 与 相 关 的 元 素 有 关 ) = W_i^{(2)} f\prime(z_i^{(2)})a_j^{(1)} (只与相关的元素有关) =Wi(2)f′(zi(2))aj(1)(只与相关的元素有关)
= δ i ( 2 ) a j ( 1 ) =\delta_i^{(2)}a_j^{(1)} =δi(2)aj(1)
从上式我们可以看到,梯度减少到 δ i ( 2 ) \delta_i^{(2)} δi(2)和 a j ( 1 ) a_j^{(1)} aj(1)的乘积, δ i ( 2 ) \delta_i^{(2)} δi(2)是第2层第 i i i个神经元处累积得到的后向传播误差, a j ( 1 ) a_j^{(1)} aj(1)是第2层第 i i i个神经元被 W i j W_{ij} Wij规约后的输入。
下面我们从 “误差共享/分布”这个概念来更好的理解上面对 W 14 ( 1 ) W_{14}^{(1)} W14(1)的更新:
- 首先 ,我们在 a 1 ( 3 ) a_1^{(3)} a1(3) 处收到了误差为1的信号。
- 然后,我们用此处神经元的局部梯度乘以这个误差,这个神经元的作用是将 z 1 ( 3 ) z_1^{(3)} z1(3) 映射到 a 1 ( 3 ) a_1^{(3)} a1(3),正巧在这个例子中也为1,所以误差 = 1, 此处神经元的累积传播误差 δ 1 ( 3 ) = 1 \delta_1^{(3)} = 1 δ1(3)=1。
- 这时误差传播到达 z 1 ( 3 ) z_1^{(3)} z1(3),现在我们需要分发这个误差信号,所以误差传到了 a 1 ( 2 ) a_1^{(2)} a1(2) 。
- 在分发的过程中,误差信号的总量为 ( δ 1 ( 3 ) = 1 ) ∗ W 1 ( 2 ) = W 1 ( 2 ) (\delta_1^{(3)} = 1) * W_1^{(2)} = W_1^{(2)} (δ1(3)=1)∗W1(2)=W1(2)。这样, a 1 ( 2 ) a_1^{(2)} a1(2)处的误差 = W 1 ( 2 ) W_1^{(2)} W1(2)。
- 同步骤2,在映射 z 1 ( 2 ) z_1^{(2)} z1(2)到 a 1 ( 2 ) a_1^{(2)} a1(2)这个神经元处,仍然是将误差乘以这个神经元的局部梯度,这个局部梯度正好是 f ′ ( z 1 ( 2 ) ) f\prime(z_1^{(2)}) f′(z1(2))。
- 这时得到 z 1 2 z_1^{2} z12处的误差 = f ′ ( z 1 ( 2 ) ) W 1 ( 2 ) f\prime(z_1^{(2)})W_1^{(2)} f′(z1(2))W1(2),累积传播误差 $\delta_1^{(2)} =f\prime(z_1{(2)})W_1{(2)} $。
- 继续向前分发误差,因为只有输入 a 4 ( 1 ) a_4^{(1)} a4(1)与 W 14 ( 1 ) W_{14}^{(1)} W14(1)有关,所以到这里只要误差乘以 a 4 ( 1 ) a_4^{(1)} a4(1)即可。
- 这时得到误差 = a 4 ( 1 ) f ′ ( z 1 ( 2 ) W 1 ( 2 ) a_4^{(1)}f\prime(z_1^{(2)}W_1^{(2)} a4(1)f′(z1(2)W1(2)。
总得来看,传播过程的误差 = a 4 ( 1 ) ∗ f ′ ( z 1 ( 2 ) ) ∗ W 1 ( 2 ) ∗ 1 ∗ 1 a_4^{(1)}*f\prime(z_1^{(2)})*W_1^{(2)}*1*1 a4(1)∗f′(z1(2))∗W1(2)∗1∗1,我们得到的结果和用公式推导得到的结果一样。
总结:我们可以使用两种方法推导参数梯度:链式法则推导或者误差共享和分发。两种方法做的工作是一样的,我们可以借助两者来互相加深理解。
对偏置 b i ( 1 ) b_i^{(1)} bi(1)求梯度:
从数学角度来看,到 z 1 ( 2 ) z_1^{(2)} z1(2)处对偏置求导和对权重求导是一样的,但是与 b i b_i bi相乘的是1,所以,第 k k k层第 i i i个神经元的偏置梯度是 δ i ( k ) \delta_i^{(k)} δi(k)。
例如,我们把上面的公式中对 W 14 ( 1 ) W_{14}^{(1)} W14(1)求导换成对 b 1 ( 1 ) b_1^{(1)} b1(1)求导,得到的梯度为 f ′ ( z 1 ( 2 ) ) W 1 ( 2 ) f\prime(z_1^{(2)})W_1^{(2)} f′(z1(2))W1(2)。
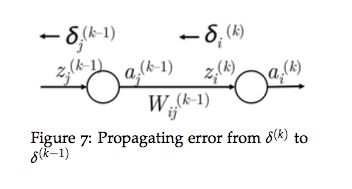
传播 δ ( k ) \delta^{(k)} δ(k)到 δ ( k − 1 ) \delta^{(k-1)} δ(k−1)的通用步骤:
首先我们看下示意图,结合示意图再看后面讲解的步骤会更清楚:
- 首先,我们有从 z i ( k ) z_i^{(k)} zi(k)处往后传播的误差 δ i ( k ) \delta_i^{(k)} δi(k),如上左图。
- 然后将误差传播到 a j ( k − 1 ) a_j^{(k-1)} aj(k−1)处,在这个过程中,误差需要乘以这条路径的权重 W i j ( k − 1 ) W_{ij}^{(k-1)} Wij(k−1)。
- 这时我们得到了 a j ( k − 1 ) a_j^{(k-1)} aj(k−1)处的误差: δ i ( k ) W i j ( k − 1 ) \delta_i^{(k)}W_{ij}^{(k-1)} δi(k)Wij(k−1)。
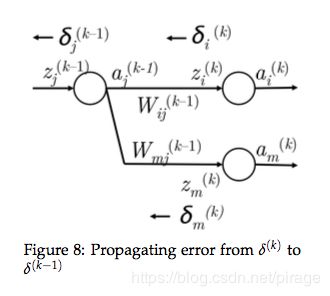
- 然而,如上右图所见, a j ( k − 1 ) a_j^{(k-1)} aj(k−1)向前传播的时候可能会传播到下一层的多个节点,所以此时 a j ( k − 1 ) a_j^{(k-1)} aj(k−1)也应该公平的收到多个节点后向传播过来的误差,例如第 k k k层第 m m m个节点的误差。
- 所以, a j ( k − 1 ) a_j^{(k-1)} aj(k−1)处接收到的误差为 δ i ( k ) W i j ( k − 1 ) + δ m ( k ) W m j ( k − 1 ) \delta_i^{(k)}W_{ij}^{(k-1)} + \delta_m^{(k)}W_{mj}^{(k-1)} δi(k)Wij(k−1)+δm(k)Wmj(k−1)。
- 实际上,写成通用的形式 ∑ i δ i ( k ) W i j ( k − 1 ) \sum_i\delta_i^{(k)}W_{ij}^{(k-1)} ∑iδi(k)Wij(k−1)。
- 现在我们得到了 a j ( k − 1 ) a_j^{(k-1)} aj(k−1)处的正确误差,我们跨过第 k − 1 k-1 k−1层第 j j j个神经元继续向后传播,这步误差需要乘以神经元的局部梯度 f ′ ( z j ( k − 1 ) ) f\prime(z_j^{(k-1)}) f′(zj(k−1))。
- 这时到达 z j ( k − 1 ) z_j^{(k-1)} zj(k−1)处的误差就是我们要求的累积误差 δ j ( k − 1 ) = f ′ ( z j ( k − 1 ) ∑ i δ i ( k ) W i j ( k − 1 ) \delta_j^{(k-1)} = f\prime(z_j^{(k-1)}\sum_i\delta_i^{(k)}W_{ij}^{(k-1)} δj(k−1)=f′(zj(k−1)∑iδi(k)Wij(k−1)。
这就是从元素角度计算后向传播的思路和方法,下面我们将结果用向量形式表达,以便于代码实现。
6. 后向传播训练–向量级别
到目前为止,我们讨论了如何对模型中给定的某个参数计算梯度,接下来我们将上述方法概括为一次更新权重矩阵和偏置向量。实际上只是对上述模型的扩展,有助于我们直观的了解矩阵级别的误差传播。
第一步,计算 W ( k ) W^{(k)} W(k)
回顾一下, W ( k ) W^{(k)} W(k)是将 a ( k ) a^{(k)} a(k)映射到 z ( k + 1 ) z^{(k+1)} z(k+1)的矩阵,我们定义参数 W i j ( k ) W_{ij}^{(k)} Wij(k)的误差梯度为 δ i ( k + 1 ) a j ( k ) \delta_i^{(k+1)}a_j^{(k)} δi(k+1)aj(k)。这样我们可以建立整个矩阵 W ( k ) W^{(k)} W(k)的误差梯度为:
Δ W ( k ) = [ δ 1 ( k + 1 ) a 1 ( k ) δ 1 ( k + 1 ) a 2 ( k ) … δ 2 ( k + 1 ) a 1 ( k ) δ 2 ( k + 1 ) a 2 ( k ) … ⋮ ⋮ ⋱ ] = δ ( k + 1 ) a ( k ) T \Delta_{W^{(k)}} = \begin{bmatrix}\delta_{1}^{(k+1)}a_1^{(k)}\ \ \delta_1^{(k+1)}a_2^{(k)}\ \ \dots\\\delta_2^{(k+1)}a_1^{(k)}\ \ \delta_2^{(k+1)a_2^{(k)}}\ \ \dots\\\vdots\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \vdots\ \ \ \ \ \ \ \ \ \ \ \ \ddots\\\end{bmatrix} = \delta^{(k+1)}a^{(k)T} ΔW(k)=⎣⎢⎢⎡δ1(k+1)a1(k) δ1(k+1)a2(k) …δ2(k+1)a1(k) δ2(k+1)a2(k) …⋮ ⋮ ⋱⎦⎥⎥⎤=δ(k+1)a(k)T
这里 δ ( k + 1 ) \delta^{(k+1)} δ(k+1)和 a ( k ) a^{(k)} a(k)都是列向量。也就是我们将矩阵的梯度写成传播到矩阵的误差向量和矩阵前向激活值的外积。
第二步,计算 δ ( k ) \delta^{(k)} δ(k)
根据前面的计算,我们很容易得到从第 ( k + 1 ) (k+1) (k+1)层到第 k k k层的误差传播为:
δ ( k ) = f ′ ( z ( k ) ) ∘ ( W ( k ) T δ ( k + 1 ) ) \delta^{(k)} = f\prime(z^{(k)})\circ(W^{(k)T}\delta^{(k+1)}) δ(k)=f′(z(k))∘(W(k)Tδ(k+1))
符号 ∘ \circ ∘表示矩阵对应元素相乘,也就是 R N ∗ R N − > R N R^N * R^N -> R^N RN∗RN−>RN。
这个公式的成立依赖于这样的假设条件:前向传播过程中,信号 z ( k ) z^{(k)} z(k)首先经过激活单元 f f f生成激活值 a ( k ) a^{(k)} a(k),然后与矩阵 W ( k ) W^{(k)} W(k)线性结合生成 z ( k + 1 ) z^{(k+1)} z(k+1)。
计算的有效性
探索了元素级别和向量级别的参数更新,我们要清楚的是,在诸如MATLAB或者Python(使用NumPy和SciPy)的科学计算环境下,向量级别的计算速度更快。所以在实现过程中我们要尽量使用向量化。
进一步讲,我们也要尽量减少冗余计算。例如, δ ( k ) \delta^{(k)} δ(k)的计算依赖于 δ ( k + 1 ) \delta^{(k+1)} δ(k+1),所以在使用 δ ( k + 1 ) \delta^{(k+1)} δ(k+1)计算 W ( k ) W^{(k)} W(k)后,保存 δ ( k + 1 ) \delta^{(k+1)} δ(k+1)以供后续使用。
循环计算 δ \delta δ的过程使得后向传播计算是一个可以负担得起的计算过程。
单层神经网络(slides)
有了上面的公式推导后再来看单层神经网络,会觉得比较简单易懂。
我们还用上节课中的例子,输入 x w i n d o w = [ x m u s e u m s x i n x P a r i s x a r e x a m a z i n g ] x_{window} = [x_{museums}\ x_{in}\ x_{Paris}\ x_{are}\ x_{amazing}] xwindow=[xmuseums xin xParis xare xamazing],我们的任务是对中心词是否是地名做分类。
单层神经网络的前向计算过程是:
s = U T a s = U^Ta s=UTa a = f ( z ) a = f(z) a=f(z) z = W x + b z = Wx+b z=Wx+b
s s s = score(“Museums in Paris are amazing”)
s c s_c sc = score(“Not all museums in Paris”)
向量维度: x ∈ R 20 ∗ 1 x\in R^{20*1} x∈R20∗1 W ∈ R 8 ∗ 20 W\in R^{8*20} W∈R8∗20 U ∈ R 8 ∗ 1 U\in R^{8*1} U∈R8∗1
目标函数:
J = m a x ( 0 , 1 − s + s c ) J = max(0, 1-s+s_c) J=max(0,1−s+sc)
后向传播训练就是 s s s 和 s c s_c sc分别对 U U U, W W W, b b b, x x x 求导数。(只需要考虑 J > 0 的情况)
对 U U U求梯度:
∂ s ∂ U = ∂ ∂ U U T a = a \frac{\partial{s}}{\partial{U}} = \frac{\partial}{\partial{U}}U^Ta = a ∂U∂s=∂U∂UTa=a
对 W W W求梯度:
无论是对单个 W i j W_{ij} Wij,还是对矩阵 W W W求导数,我们都已经推导过,这里只写结论。
∂ s ∂ W i j = U i f ′ ( z i ) x j = δ i x j \frac{\partial{s}}{\partial{W_{ij}}} = U_if\prime(z_i)x_j = \delta_ix_j ∂Wij∂s=Uif′(zi)xj=δixj
∂ J ∂ W = δ x T \frac{\partial{J}}{\partial{W}} = \delta{x^T} ∂W∂J=δxT
对 b b b求梯度:
∂ s ∂ b i = U i f ′ ( z i ) = δ i \frac{\partial{s}}{\partial{b_i}} = U_if\prime(z_i) = \delta_i ∂bi∂s=Uif′(zi)=δi
对 x x x求梯度:
对单个元素求梯度,需要考虑所有 a i a_i ai的情况,因为 x j x_j xj会影响所有的 a i a_i ai。
∂ s ∂ x j = ∑ i δ i W i j = W ⋅ j T δ \frac{\partial{s}}{\partial{x_j}} = \sum_i\delta_i W_{ij} = W_{\cdot j}^T \delta ∂xj∂s=i∑δiWij=W⋅jTδ
∂ s ∂ x = W T δ \frac{\partial s}{\partial x} = W^T\delta ∂x∂s=WTδ
隐含层 δ \delta δ的误差信息的维度与隐含层的个数相同。
每个窗口的全目标函数对参数求梯度:
上面我们考虑的是score对参数的梯度,全目标函数 J J J要结合 s s s和 s c s_c sc两种考虑,以参数 U U U为例:
∂ J ∂ U = 1 { 1 − s + s c > 0 } ( − a + a c ) \frac{\partial J}{\partial U} = 1\{1-s+s_c>0\}(-a + a_c) ∂U∂J=1{1−s+sc>0}(−a+ac)
两层神经网络(slides)
输入x和得分函数都同上,两层神经网络的前向传播过程为:
z ( 1 ) = W ( 1 ) x + b ( 1 ) z^{(1)} = W^{(1)}x + b^{(1)} z(1)=W(1)x+b(1)
a ( 1 ) = f ( z ( 1 ) ) a^{(1)} = f(z^{(1)}) a(1)=f(z(1))
z ( 2 ) = W ( 2 ) a ( 1 ) + b ( 2 ) z^{(2)} = W^{(2)}a^{(1)} + b^{(2)} z(2)=W(2)a(1)+b(2)
a ( 2 ) = f ( z ( 2 ) ) a^{(2)} = f(z^{(2)}) a(2)=f(z(2))
s = U T a ( 2 ) s = U^Ta^{(2)} s=UTa(2)
合成一个公式为: s = U T f ( W ( 2 ) f ( W ( 1 ) x + b ( 1 ) ) + b ( 2 ) ) s = U^Tf(W^{(2)}f(W^{(1)}x+b^{(1)}) + b^{(2)}) s=UTf(W(2)f(W(1)x+b(1))+b(2))
每个层传播的累积误差分别为:
δ ( 2 ) = U ∘ f ′ ( z ( 2 ) ) \delta^{(2)} = U \circ f\prime (z^{(2)}) δ(2)=U∘f′(z(2)) δ ( 1 ) = ( W ( 1 ) T δ ( 2 ) ) ∘ f ′ ( z ( 1 ) ) \delta^{(1)} = (W^{(1)T}\delta^{(2)}) \circ f\prime(z^{(1)}) δ(1)=(W(1)Tδ(2))∘f′(z(1))
对 W ( 2 ) W^{(2)} W(2)的梯度同一层神经网络一样:
∂ s ∂ W ( 2 ) = δ ( 2 ) a ( 1 ) T \frac{\partial s}{\partial W^{(2)}} = \delta^{(2)}a^{(1)T} ∂W(2)∂s=δ(2)a(1)T