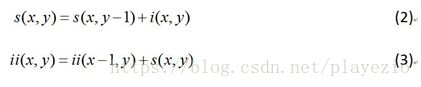haar+adaboost结合讲解（偏重原理）

【这是一篇之前总结的文档，大部分来源于csdn和文献，如有未标明引用，请联系我加上。】

 

目录

1 Adaboost方法的引入

1.1 Boosting方法的提出和发展

1.2 AdaBoost算法的提出

1.3 级联分类器介绍

2 矩形特征

2.1 Haar特征\矩形特征

2.2 子窗口内的条件矩形，矩形特征个数的计算

2.3条件矩形的数量

3 积分图

3.1 积分图的概念

3.2 利用积分图计算特征值

3.3计算特征值

4 级联分类器与检测过程

4.1 弱分类器

4.2 训练强分类器

4.3弱分类器使用Haar特征进行分类

4.4 弱分类器的训练及选取

4.5 强分类器

4.6 图像检测过程

 

 

1 Adaboost方法的引入

1.1 Boosting方法的提出和发展

在了解Adaboost方法之前，先了解一下Boosting方法。

回答一个是与否的问题，随机猜测可以获得50%的正确率。如果一种方法能获得比随机猜测稍微高一点的正确率，则就可以称该得到这个方法的过程为弱学习；如果一个方法可以显著提高猜测的正确率，则称获取该方法的过程为强学习。

1994年，Kearns和Valiant证明，在Valiant的PAC（ProbablyApproximately Correct）模型中，只要数据足够多，就可以将弱学习算法通过集成的方式提高到任意精度。实际上，1990年，SChapire就首先构造出一种多项式级的算法，将弱学习算法提升为强学习算法，就是最初的Boosting算法。

Boosting意思为提升、加强，现在一般指将弱学习提升为强学习的一类算法。1993年，Drucker和Schapire首次以神经网络作为弱学习器，利用Boosting算法解决实际问题。前面指出，将弱学习算法通过集成的方式提高到任意精度，是Kearns和Valiant在1994年才证明的，虽然Boosting方法在1990年已经提出，但它的真正成熟，也是在1994年之后才开始的。1995年，Freund提出了一种效率更高的Boosting算法。

1.2 AdaBoost算法的提出

1995年，Freund和Schapire提出了Adaboost算法，是对Boosting算法的一大提升。Adaboost是Boosting家族的代表算法之一，全称为Adaptive Boosting。

Adaptively，即适应地，该方法根据弱学习的结果反馈适应地调整假设的错误率，所以Adaboost不需要预先知道假设的错误率下限。也正因为如此，它不需要任何关于弱学习器性能的先验知识，而且和Boosting算法具有同样的效率，所以在提出之后得到了广泛的应用。

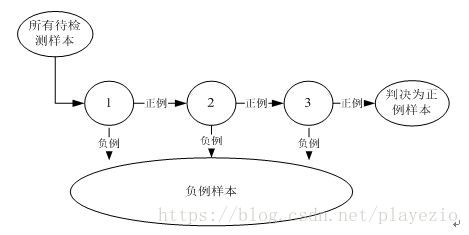
首先，Adaboost是一种基于级联分类模型的分类器。级联分类模型可以用图1表示：

图1

1.3 级联分类器介绍

级联分类器就是将多个强分类器连接在一起进行操作。每一个强分类器都由若干个弱分类器加权组成，

例如，有些强分类器可能包含10个弱分类器，有些则包含20个弱分类器，一般情况下一个级联用的强分类器包含20个左右的弱分类器，然后在将10个强分类器级联起来，就构成了一个级联强分类器，这个级联强分类器中总共包括200弱分类器。因为每一个强分类器对负样本的判别准确度非常高，所以一旦发现检测到的目标位负样本，就不在继续调用下面的强分类器，减少了很多的检测时间。因为一幅图像中待检测的区域很多都是负样本，这样由级联分类器在分类器的初期就抛弃了很多负样本的复杂检测，所以级联分类器的速度是非常快的；只有正样本才会送到下一个强分类器进行再次检验，这样就保证了最后输出的正样本的伪正(falsepositive)的可能性非常低。

也有一些情况下不适用级联分类器，就简单的使用一个强分类器的情况，这种情况下一般强分类器都包含200个左右的弱分类器可以达到最佳效果。不过级联分类器的效果和单独的一个强分类器差不多，但是速度上却有很大的提升。

级联结构分类器由多个弱分类器组成，每一级都比前一级复杂。每个分类器可以让几乎所有的正例通过，同时滤除大部分负例。这样每一级的待检测正例就比前一级少，排除了大量的非检测目标，可大大提高检测速度。

其次，Adaboost是一种迭代算法。初始时，所有训练样本的权重都被设为相等，在此样本分布下训练出一个弱分类器。在第（=1,2,3,…T，T为迭代次数）次迭代中，样本的权重由第-1次迭代的结果而定。在每次迭代的最后，都有一个调整权重的过程，被分类错误的样本将得到更高的权重。这样分错的样本就被突出出来，得到一个新的样本分布。在新的样本分布下，再次对弱分类器进行训练，得到新的弱分类器。经过T次循环，得到T个弱分类器，把这T个弱分类器按照一定的权重叠加起来，就得到最终的强分类器。

2 矩形特征

2.1 Haar特征\矩形特征

AdaBoost算法的实现，采用的是输入图像的矩形特征，也叫Haar特征。下面简要介绍矩形特征的特点。

影响Adaboost检测训练算法速度很重要的两方面是特征的选取和特征值的计算。脸部的一些特征可以由矩形特征简单地描绘。用图2示范：

图2

图2中两个矩形特征，表示出人脸的某些特征。比如中间一幅表示眼睛区域的颜色比脸颊区域的颜色深，右边一幅表示鼻梁两侧比鼻梁的颜色要深。同样，其他目标，如眼睛等，也可以用一些矩形特征来表示。使用特征比单纯地使用像素点具有很大的优越性，并且速度更快。

在给定有限的数据情况下，基于特征的检测能够编码特定区域的状态，而且基于特征的系统比基于象素的系统要快得多。
    矩形特征对一些简单的图形结构，比如边缘、线段，比较敏感，但是其只能描述特定走向（水平、垂直、对角）的结构，因此比较粗略。如上图，脸部一些特征能够由矩形特征简单地描绘，例如，通常，眼睛要比脸颊颜色更深；鼻梁两侧要比鼻梁颜色要深；嘴巴要比周围颜色更深。

对于一个24×24检测器，其内的矩形特征数量超过160,000个，必须通过特定算法甄选合适的矩形特征，并将其组合成强分类器才能检测人脸。

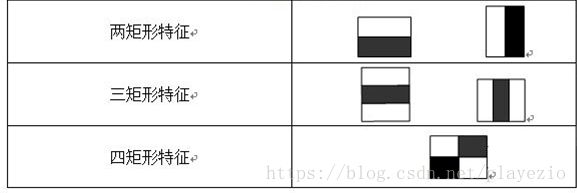
常用的矩形特征有三种：两矩形特征、三矩形特征、四矩形特征，如图3：

图3

由图表可以看出，两矩形特征反映的是边缘特征，三矩形特征反映的是线性特征、四矩形特征反映的是特定方向特征。

特征模板的特征值定义为：白色矩形像素和减去黑色矩形像素和。接下来，要解决两个问题，1：求出每个待检测子窗口中的特征个数。2：求出每个特征的特征值。

子窗口中的特征个数即为特征矩形的个数。训练时，将每一个特征在训练图像子窗口中进行滑动计算，获取各个位置的各类矩形特征。在子窗口中位于不同位置的同一类型矩形特征，属于不同的特征。可以证明，在确定了特征的形式之后，矩形特征的数量只与子窗口的大小有关^[11]。在24×24的检测窗口中，矩形特征的数量约为160,000个。

特征模板可以在子窗口内以“任意”尺寸“任意”放置，每一种形态称为一个特征。找出子窗口所有特征，是进行弱分类训练的基础。

2.2 子窗口内的条件矩形，矩形特征个数的计算

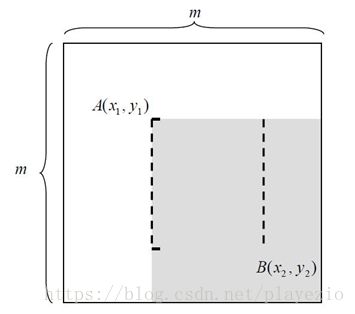
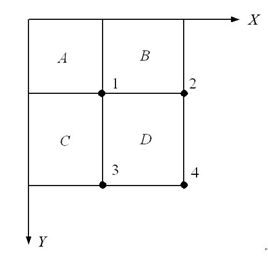
如图4所示的一个m*m大小的子窗口，可以计算在这么大的子窗口内存在多少个矩形特征。

图4

以m×m像素分辨率的检测器为例，其内部存在的满足特定条件的所有矩形的总数可以这样计算：
    对于m×m子窗口，我们只需要确定了矩形左上顶点A(x1,y1)和右下顶点B(x2,63)，即可以确定一个矩形；如果这个矩形还必须满足下面两个条件（称为(s,t)条件，满足(s,t)条件的矩形称为条件矩形）：

1) x方向边长必须能被自然数s整除（能均等分成s段）；

2) y方向边长必须能被自然数t整除（能均等分成t段）；

则，这个矩形的最小尺寸为s×t或t×s，最大尺寸为[m/s]·s×[m/t]·t或[m/t]·t×[m/s]·s；其中[]为取整运算符。

2.3条件矩形的数量

我们通过下面两步就可以定位一个满足条件的矩形：

由上分析可知，在m×m子窗口中，满足(s,t)条件的所有矩形的数量为：

 

实际上，(s,t)条件描述了矩形特征的特征，下面列出了不同矩形特征对应的(s,t)条件：

下面以24×24子窗口为例，具体计算其特征总数量：

下面列出了，在不同子窗口大小内，特征的总数量：

 

3 积分图

3.1 积分图的概念

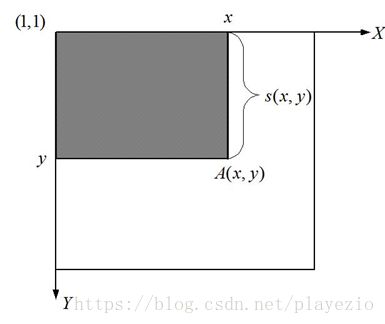
在获取了矩形特征后，要计算矩形特征的值。Viola等人提出了利用积分图求特征值的方法。积分图的概念可用图5表示：

坐标A(x,y)的积分图是其左上角的所有像素之和（图中的阴影部分）。定义为：

其中ii(x,y)表示积分图，i(x,y)表示原始图像，对于彩色图像，是此点的颜色值；对于灰度图像，是其灰度值，范围为0~255。

图5

在上图中，A(x,y)表示点(x,y)的积分图；s(x,y)表示点(x,y)的y方向的所有原始图像之和。积分图也可以用公式（2）和公式（3）得出：

3.2 利用积分图计算特征值

3.3计算特征值

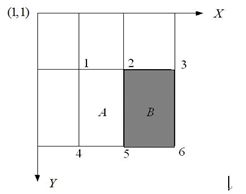
由上一节已经知道，一个区域的像素值，可以由该区域的端点的积分图来计算。由前面特征模板的特征值的定义可以推出，矩形特征的特征值可以由特征端点的积分图计算出来。以“两矩形特征”中的第二个特征为例，如下图，使用积分图计算其特征值：

4 级联分类器与检测过程

4.1 弱分类器

在确定了训练子窗口中的矩形特征数量和特征值后，需要对每一个特征f，训练一个弱分类器h(x,f,p,O)。

特别说明：在前期准备训练样本的时候，需要将样本归一化和灰度化到20*20的大小，这样每个样本的都是灰度图像并且样本的大小一致，保证了每一个Haar特征（描述的是特征的位置）都在每一个样本中出现。

4.2 训练强分类器

在训练强分类器中，T表示的是强分类器中包含的弱分类器的个数。当然，如果是采用级联分类器，这里的强分类器中的弱分类器的个数可能会比较少，多个强分类器在级联起来。

在c(2)步骤中，“每个特征f”指的是在20*20大小的训练样本中所有的可能出现的矩形特征，大概要有80,000中，所有的这些都要进行计算。也就是要计算80,000个左右的弱分类器，在选择性能好的分类器。

训练强分类器的步骤如图：

4.3弱分类器使用Haar特征进行分类

对于本算法中的矩形特征来说，弱分类器的特征值f(x)就是矩形特征的特征值。由于在训练的时候，选择的训练样本集的尺寸等于检测子窗口的尺寸，检测子窗口的尺寸决定了矩形特征的数量，所以训练样本集中的每个样本的特征相同且数量相同，而且一个特征对一个样本有一个固定的特征值。

对于理想的像素值随机分布的图像来说，同一个矩形特征对不同图像的特征值的平均值应该趋于一个定值k。
  这个情况，也应该发生在非人脸样本上，但是由于非人脸样本不一定是像素随机的图像，因此上述判断会有一个较大的偏差。

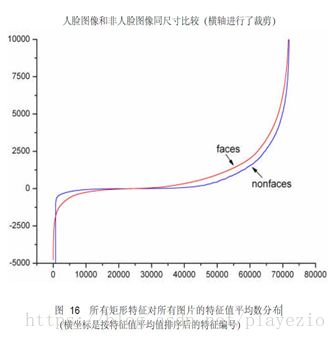
对每一个特征，计算其对所有的一类样本(人脸或者非人脸)的特征值的平均值，最后得到所有特征对所有一类样本的平均值分布。

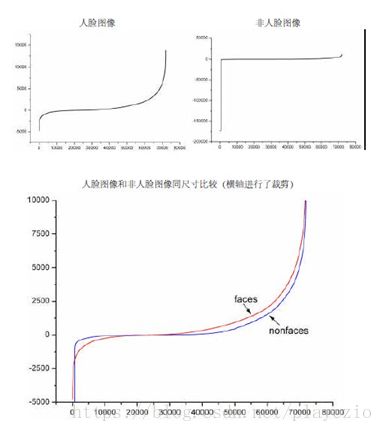
下图显示了20×20子窗口里面的全部78,460个矩形特征对全部2,706个人脸样本和4,381个非人脸样本6的特征值平均数的分布图。由分布看出，特征的绝大部分的特征值平均值都是分布在0前后的范围内。出乎意料的是，人脸样本与非人脸样本的分布曲线差别并不大，不过注意到特征值大于或者小于某个值后，分布曲线出现了一致性差别，这说明了绝大部分特征对于识别人脸和非人脸的能力是很微小的，但是存在一些特征及相应的阈值，可以有效地区分人脸样本与非人脸样本。

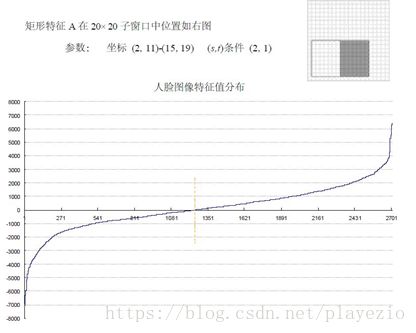
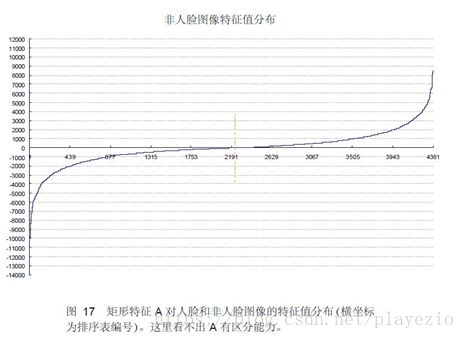
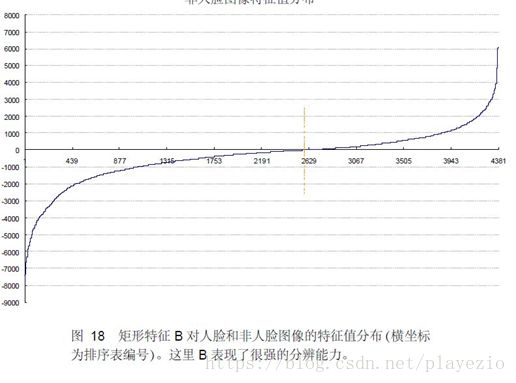
为了更好地说明问题，我们从78,460个矩形特征中随机抽取了两个特征A和B，这两个特征遍历了2,706个人脸样本和4,381个非人脸样本，计算了每张图像对应的特征值，最后将特征值进行了从小到大的排序，并按照这个新的顺序表绘制了分布图如下所示：

可以看出，矩形特征A在人脸样本和非人脸样本中的特征值的分布很相似，所以区分人脸和非人脸的能力很差。

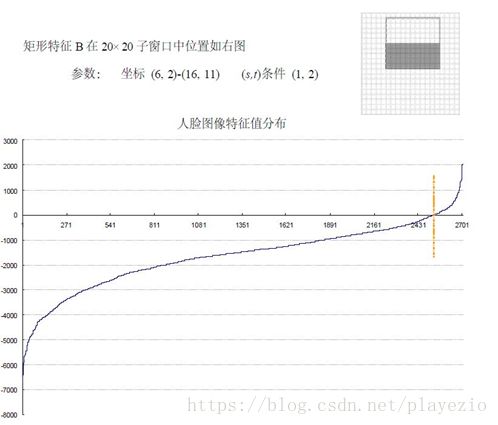
下面看矩形特征B在人脸样本和非人脸样本中特征值的分布：

可以看出，矩形特征B的特征值分布，尤其是0点的位置，在人脸样本和非人脸样本中差别比较大，所以可以更好的实现对人脸分类。

由上述的分析，阈值q的含义就清晰可见了。而方向指示符p用以改变不等号的方向。

一个弱学习器（一个特征）的要求仅仅是：它能够以稍低于50%的错误率来区分人脸和非人脸图像，因此上面提到只能在某个概率范围内准确地进行区分就
已经完全足够。按照这个要求，可以把所有错误率低于50%的矩形特征都找到（适当地选择阈值，对于固定的训练集，几乎所有的矩形特征都可以满足上述要求）。每轮训练，将选取当轮中的最佳弱分类器（在算法中，迭代T次即是选择T个最佳弱分类器），最后将每轮得到的最佳弱分类器按照一定方法提升（Boosting）为强分类器

4.4 弱分类器的训练及选取

训练一个弱分类器（特征f）就是在当前权重分布的情况下，确定f的最优阈值，使得这个弱分类器（特征f）对所有训练样本的分类误差最低。
选取一个最佳弱分类器就是选择那个对所有训练样本的分类误差在所有弱分类器中最低的那个弱分类器（特征）。

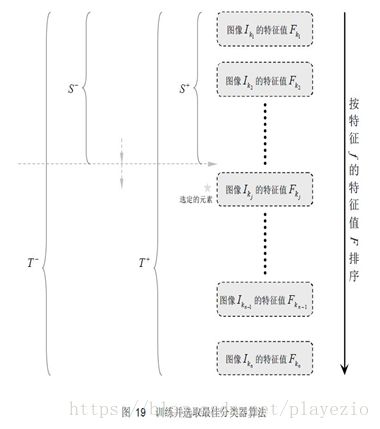
对于每个特征f，计算所有训练样本的特征值，并将其排序。通过扫描一遍排好序的特征值，可以为这个特征确定一个最优的阈值，从而训练成一个弱分类器。具体来说，对排好序的表中的每个元素，计算下面四个值：

4.5 强分类器

注意，这里所说的T=200个弱分类器，指的是非级联的强分类器。若果是用级联的强分类器，则每个强分类器的弱分类器的个数会相对较少。

一般学术界所说的级联分类器，都是指的是级联强分类器，一般情况有10个左右的强分类器，每个强分类有10-20个弱分类器。当然每一层的强分类器中弱分类器的个数可以不相等，可以根据需要在前面的层少放一些弱分类器，后面的层次逐渐的增加弱分类器的个数。

4.6 图像检测过程

在对输入图像进行检测的时候，一般输入图像都会比20*20的训练样本大很多。在Adaboost算法中采用了扩大检测窗口的方法，而不是缩小图片。

为什么扩大检测窗口而不是缩小图片呢，在以前的图像检测中，一般都是将图片连续缩小十一级，然后对每一级的图像进行检测，最后在对检测出的每一级结果进行汇总。然而，有个问题就是，使用级联分类器的AdaBoost的人脸检测算法的速度非常的快，不可能采用图像缩放的方法，因为仅仅是把图像缩放11级的处理，就要消耗一秒钟至少，已经不能达到Adaboost的实时处理的要求了。

因为Haar特征具有与检测窗口大小无关的特性（想要了解细节还要读一下原作者的文献），所以可以将检测窗口进行级别方法。

在检测的最初，检测窗口和样本大小一致，然后按照一定的尺度参数（即每次移动的像素个数，向左然后向下）进行移动，遍历整个图像，标出可能的人脸区域。遍历完以后按照指定的放大的倍数参数放大检测窗口，然后在进行一次图像遍历；这样不停的放大检测窗口对检测图像进行遍历，直到检测窗口超过原图像的一半以后停止遍历。因为整个算法的过程非常快，即使是遍历了这么多次，根据不同电脑的配置大概处理一幅图像也就是几十毫秒到一百毫秒左右。

在检测窗口遍历完一次图像后，处理重叠的检测到的人脸区域，进行合并等操作。