TensorFlow实战笔记之（3）：神经网络优化策略

根据我前面两篇博客Softmax Regression 实现手写数字识别和简单神经网络 实现手写数字识别的结果，使用单层的Softmax Regression进行手写数字识别的准确率约为92%，而加了一层隐层之后，准确率只有80%左右，令人感到意外，因为一般网络越深，分类效果应该越好才对。不过简单分析一下，原因可能就是加了一层隐层之后参数数量变大，容易产生过拟合等。单层的Softmax Regression网络其参数个数为784*10+10=7850，而增加一层15个神经元的隐层之后，参数个数变为（784*15+15）+（15*10+10）=11935。

为了挖掘单隐层神经网络的潜力，加入了一些神经网络的优化策略，包括指数衰减学习率和正则化，下面加以介绍，并在最后给出了代码和优化结果。

一、指数衰减学习率

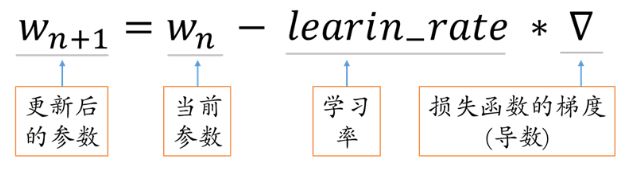
学习率是指每次参数更新的幅度，如下。

学习率设置的过小则参数更新太慢，学习效率低；学习率设置的太大，则后期容易产生振荡，难以收敛。但在参数更新前期，参数距离最优参数较远，希望学习率设置的大些；而在参数更新后期，参数距离最优参数较近，为了避免产生振荡，希望参数设置的小些。由此可见，学习率设置成固定值并不是最好的。

指数衰减学习率是根据运行的轮数动态调整学习率的一种方法，在TensorFlow中表示如下：

tf.train.exponential_decay(
    learning_rate,        # 学习率初始值
    global_step,          # 当前训练总轮数（不能为负）
    decay_steps,          # 衰减步长（必须为正），即多少轮更新一次学习率
    decay_rate,           # 衰减率，一般取值范围为(0,1)
    staircase=False,      # True:阶梯型衰减, False:平滑衰减
    name=None             # 操作的可选名称，默认为'ExponentialDecay'
)

 学习率的计算公式为：

decayed_learning_rate = learning_rate *
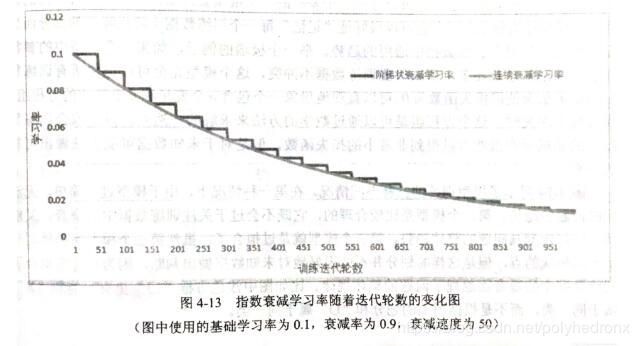
                        decay_rate ^ (global_step / decay_steps)

注意当staircase为Ture时，global_step / decay_steps是一个整数，衰减率为阶梯函数 ，如下。

应用示例：

...
global_step = tf.Variable(0, trainable=False)
starter_learning_rate = 0.1
learning_rate = tf.train.exponential_decay(starter_learning_rate, global_step, 100000, 0.96, staircase=True)
# Passing global_step to minimize() will increment it at each step.
learning_step = (
    tf.train.GradientDescentOptimizer(learning_rate)
    .minimize(...my loss..., global_step=global_step)
)

 二、正则化

当模型比较复杂时，它会去拟合数据中的噪声而损失了一定的通用性，即产生了过拟合。为了避免过拟合问题，常用的方法是加入正则化项，即在损失函数中加入刻画模型复杂程度的指标，将优化目标定义为J(θ)+λR(w)，其中R(w)刻画的是模型的复杂程度，包括了权重项w不包括偏置项b，λ表示模型复杂损失在总损失中的比例。

常用的正则化有L1正则化和L2正则化，

其中，L1正则化会让参数变得更稀疏，L2则不会。一个含有L2正则化的损失函数的例子：

loss = tf.reduce_mean(tf.square(y_ - y)) + tf.contrib.layers.l2_regularizer(lambda)(w)

其中损失函数的第一项一般为预测输出和真实label之间的均方误差或交叉熵，第二项即为L2正则化项，lambda表示正则化项的权重，也就是J(θ)+λR(w)中的λ，w为需要计算正则化损失的参数。

TensorFlow中tf.contrib.layers.l2_regularizer函数的定义：

tf.contrib.layers.l2_regularizer(
    scale,  # 正则项的系数
    scope=None  # 可选的scope name
)

在简单的神经网络中，加入正则化来计算损失函数还是比较容易的。当神经网络变得非常复杂（层数很多）的时候，那么在损失函数中加入正则化的就会变得非常的复杂，使得损失函数的定义变得很长，从而还会导致程序的可读性变差，如这个例子。而且还有可能，当神经网络变得复杂的时候，定义网络结构的部分和计算损失函数的部分不在同一个函数中，这样就会使得计算损失函数不方便。TensorFlow提供了集合的方式，通过在计算图中保存一组实体，来解决这一类问题。下面是一个应用示例。

import tensorflow as tf


# 获取一层神经网络的权重，并将权重的L2正则化损失加入到集合中
def get_weight(shape, lamda):
    # 定义变量
    var = tf.Variable(tf.random_normal(shape=shape), dtype=tf.float32)
    # 将变量的L2正则化损失添加到集合中
    tf.add_to_collection("losses", tf.contrib.layers.l2_regularizer(lamda)(var))
    return var


if __name__ == "__main__":
    # 定义输入节点
    x = tf.placeholder(tf.float32, shape=(None, 2))
    # 定义输出节点
    y_ = tf.placeholder(tf.float32, shape=(None, 1))
    # 定义每次迭代数据的大小
    batch_size = 8
    # 定义五层神经网络，并设置每一层神经网络的节点数目
    layer_dimension = [2, 10, 10, 10, 1]
    # 获取神经网络的层数
    n_layers = len(layer_dimension)
    # 定义神经网络第一层的输入
    cur_layer = x
    # 当前层的节点个数
    in_dimension = layer_dimension[0]
    # 通过循环来生成5层全连接的神经网络结构
    for i in range(1, n_layers):
        # 定义神经网络上一层的输出，下一层的输入
        out_dimension = layer_dimension[i]
        # 定义当前层中权重的变量，并将变量的L2损失添加到计算图的集合中
        weight = get_weight([in_dimension, out_dimension], 0.001)
        # 定义偏置项
        bias = tf.Variable(tf.constant(0.1, shape=[out_dimension]))
        # 使用RELU激活函数
        cur_layer = tf.nn.relu(tf.matmul(cur_layer, weight) + bias)
        # 定义下一层神经网络的输入节点数
        in_dimension = layer_dimension[i]
    # 定义均方差的损失函数
    mse_loss = tf.reduce_mean(tf.square(y_ - cur_layer))
    # 将均方误差函数添加到集合
    tf.add_to_collection("losses", mse_loss)
    # 获取整个模型的损失函数,tf.get_collection("losses")返回集合中定义的损失
    # 将整个集合中的损失相加得到整个模型的损失函数
    loss = tf.add_n(tf.get_collection("losses"))

其中，

tf.add_to_collection(name, value) 用来把一个value放入名称是'name'的集合，组成一个列表。

tf.get_collection(key, scope=None) 用来获取一个名称是‘key’的集合中的所有元素，返回的是一个列表，列表的顺序是按照变量放入集合中的先后; scope参数可选，表示的是名称空间（名称域），如果指定，就返回名称域中所有放入‘key’的变量的列表，不指定则返回所有变量。

tf.add_n(inputs, name=None), 把所有 ‘inputs’列表中的所有变量值相加，name可选，是操作的名称。

三、程序和结果

程序运行版本为：python-->3.7.3，tensorflow-->1.13.1 

隐层神经元个数仍设为15个，隐层激活函数改为Relu函数。weight初始化为服从正态分布的随机数，bias初始化为常数0.1。

使用指数衰减学习率，学习率初始值设为0.01，衰减步长设为训练集的batch个数，衰减率设为0.99，优化算法采用Adam。

加入了正则化，正则项的系数设为0.0001。batch的大小为100，训练次数为100000，程序如下。

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import matplotlib.pyplot as plt

# move warning
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'
old_v = tf.logging.get_verbosity()
tf.logging.set_verbosity(tf.logging.ERROR)

# neural network parameters
INPUT_NODE = 784
LAYER1_NODE = 15
OUTPUT_NODE = 10

# exponential attenuation learning rate
LEARNING_RATE_BASE = 0.01
LEARNING_RATE_DECAY = 0.99

# regularization coefficient
LAMDA = 0.0001

# training parameters
BATCH_SIZE = 100
TRAINING_STEPS = 100000


# initialize weights and add regularization
def get_weight(shape, lamda):
    weights = tf.Variable(tf.random_normal(shape=shape), dtype=tf.float32)
    tf.add_to_collection("losses", tf.contrib.layers.l2_regularizer(lamda)(weights))
    return weights


# read data
mnist = input_data.read_data_sets('MNIST_data/', one_hot=True)

# create model
# input layer
x = tf.placeholder(tf.float32, [None, INPUT_NODE])  # input images
y_ = tf.placeholder(tf.float32, [None, OUTPUT_NODE])  # input labels

# hidden layer
w1 = get_weight([INPUT_NODE, LAYER1_NODE], LAMDA)
b1 = tf.Variable(tf.constant(0.1, shape=[LAYER1_NODE]))
y1 = tf.nn.relu(tf.matmul(x, w1) + b1)

# output layer
w2 = get_weight([LAYER1_NODE, OUTPUT_NODE], LAMDA)
b2 = tf.Variable(tf.constant(0.1, shape=[OUTPUT_NODE]))
y2 = tf.nn.softmax(tf.matmul(y1, w2) + b2)

# loss function
cross_entropy = tf.reduce_mean(tf.nn.softmax_cross_entropy_with_logits(labels=y_, logits=y2))
tf.add_to_collection('losses', cross_entropy)
loss = tf.add_n(tf.get_collection('losses'))

# optimization algorithm
global_step = tf.Variable(0, trainable=False)
learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE, global_step,
                                           mnist.train.num_examples / BATCH_SIZE, LEARNING_RATE_DECAY)
train_step = tf.train.AdamOptimizer(learning_rate=learning_rate).minimize(loss, global_step=global_step)

# new session
sess = tf.Session()
sess.run(tf.global_variables_initializer())

# train
losss = []
accurs = []
steps = []
rates = []
correct_prediction = tf.equal(tf.argmax(y_, 1), tf.argmax(y2, 1))
accuracy = tf.reduce_mean(tf.cast(correct_prediction, tf.float32))
for i in range(TRAINING_STEPS):
    batch_xs, batch_ys = mnist.train.next_batch(BATCH_SIZE)
    _, now_loss, step, now_learn_rate = sess.run([train_step, loss, global_step, learning_rate],
                                                 feed_dict={x: batch_xs, y_: batch_ys})

    if i % 1000 == 0:
        accur = sess.run(accuracy, feed_dict={x: mnist.test.images, y_: mnist.test.labels})
        accurs.append(accur)
        losss.append(now_loss)
        steps.append(step)
        rates.append(now_learn_rate)
        print('learning_rate: ', now_learn_rate)
        print('Steps: {} loss: {}'.format(step, now_loss))
        print('Steps: {} accuracy: {}'.format(step, accur))

# learning rate
plt.figure()
plt.plot(steps, rates)
plt.xlabel('Number of steps')
plt.ylabel('Learning rate')

# loss
plt.figure()
plt.plot(steps, losss)
plt.xlabel('Number of steps')
plt.ylabel('Loss')

# accuracy
plt.figure()
plt.plot(steps, accurs)
plt.hlines(1, 0, max(steps), colors='r', linestyles='dashed')
plt.xlabel('Number of steps')
plt.ylabel('Accuracy')
plt.show()

tf.logging.set_verbosity(old_v)

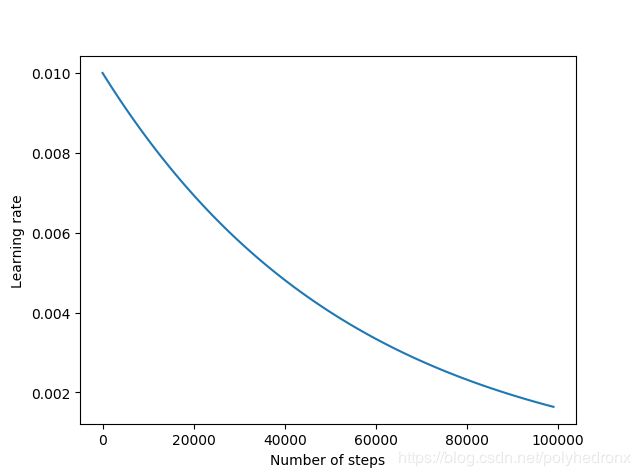
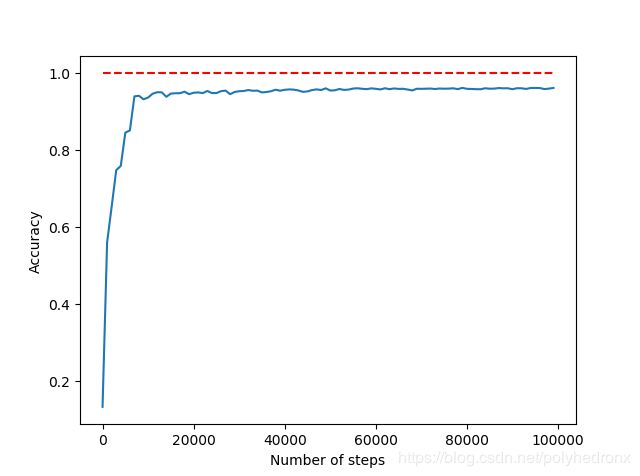
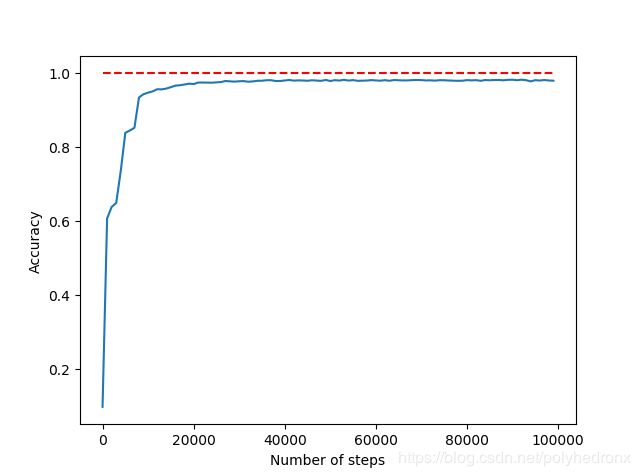
学习率、Loss和测试集准确度随训练次数变化的曲线如下图所示。

由图可知，学习率指数地下降，Loss下降地很快，测试集准确度也很快稳定下来，最终准确度约为96%，相比于上一篇博文中的80%有了很大的提升。

 

 

 此外，通过增加隐层神经元的个数可以进一步提高神经网络的性能。例如，我们将隐层神经元由15个提高到100个，学习率初始值设为0.005，则最终准确度为98%左右，如下图所示。

参考文献

1. TensorFlow神经网络优化策略

2.https://www.tensorflow.org/api_docs/python/tf/train/exponential_decay

3.『TensorFlow』正则化添加方法整理

4.Tensorflow中实现正则化