【2017CS231n】第十讲:循环神经网络(RNN)
一.RNN
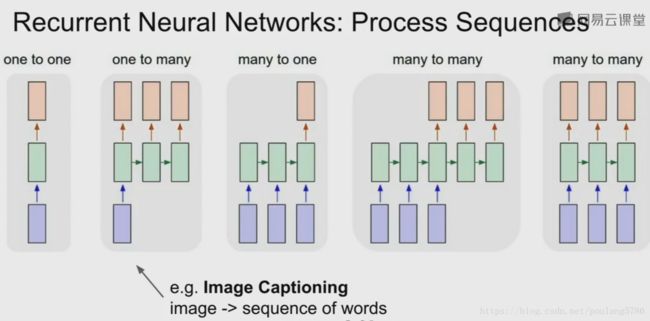
最左边是Vanilla前馈网络,固定尺寸的输入,给出单一的输出结果。
对来说RNN我们有一对多的模型,固定的输入对象,输出是可变长度的序列(例如一段描述,不同的描述对应不同的单词数量,所以需要可变的输出长度)。
多对一模型,输入的尺寸是可变的,例如输入一段文字,输出情感的分析(积极或消极);或者输入是一个视频,帧数是可变量,输入的视频有可变的时间,最后输出判断视频发生了什么活动。
多对多模型,输入和输出的尺寸都是可变的。机器翻译中,输入英文句子长度可变,输出是法语句子长度可变。同时容纳输入和输出的可变长度序列。
最后一种多对多模型,当输入是视频时,输出时对每一帧都做分类决策。
1.1例子
Vanilla RNN:
前一时刻的状态ht-1乘权重Whh,输入xt乘以权重Wxh,相加后通过tanh函数归一化到(-1,1),要得到分类结果,还需要一个权重Why。
1.2核心循环单元
每个RNN网络都有小小的循环单元,x作为输入,将其传入RNN,RNN有一个内部隐藏态,隐藏态会在RNN每次读取新的输入时更新,当模型下一次读取输入时将结果反馈至模型。
读取输入,更新隐藏态,生成输出。
循环单元的计算过程:
函数f依赖权重w,f接受隐藏态ht-1,当前态xt,输出下一个隐藏态ht。
当我们读取下一个输入时,此时的隐藏态ht作为新的输入,同时读取输入xt+1。
每次计算每次都用同样的函数和参数。
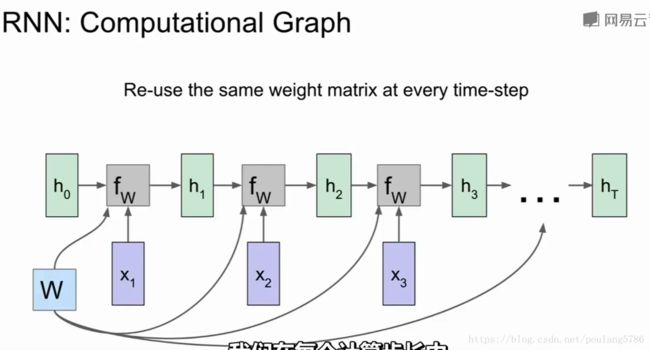
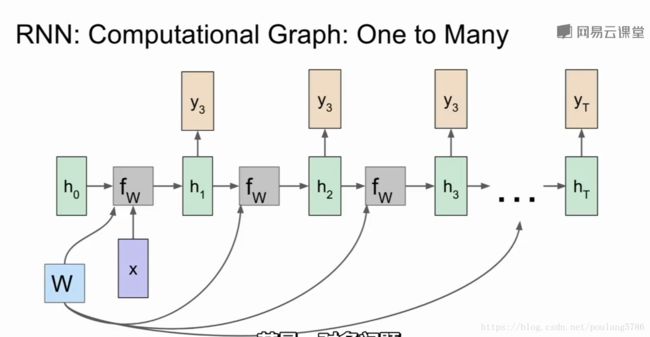
1.3RNN的计算图
每一次fw都接受不同的h和x,使用相同的权重w。
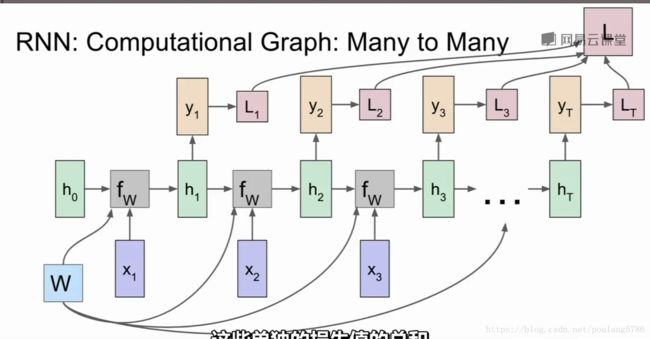
yt是可以是每一步的分类。
有了分类结果yt就可以与真实标签对比,计算损失。
最后计算最终的损失。
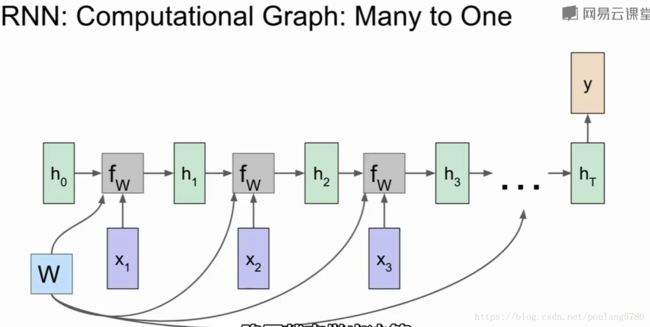
1.4不同的决策模型
多对一的情况,例如情感分析,根据网络最终的隐层状态做出决策。因为最终隐层状态包含了序列中所有的情况。
一对多的情况,接受固定长的输入项,输出不定长的输出不项,输入项会被初始化为模型初始隐层状态。
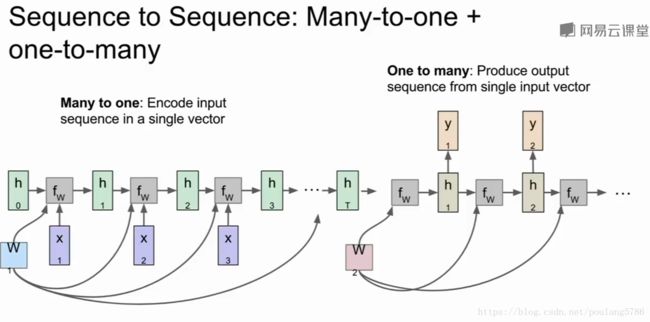
sequence to sequence
类似于机器翻译,存在编码和解码两个过程。
编码:多对一
接收一个不定长度的输入序列,句子被编码器网络编码成最终隐层状态。接下来就是解码。
解码:一对多
已经把句子编成了一个向量,输入是前面编码完成的向量,输出一个不定长序列。
二.语言模型
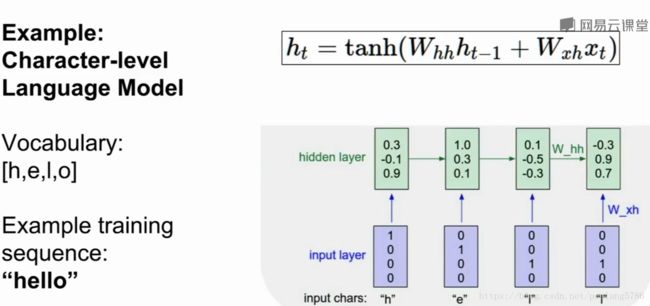
2.1例子
读取一串字符,预测文本流的下一个字符是什么。
例如输入hell,它会预测到下一个字母是o
输入helo变成向量形式,
h:1000
e:0100
l:0010
o:0001
训练的进行:h输入到网络中,做出预测输出yt,即下一个字母的可能性。通过softmax来描述损失。
序列生成过程:基于上一个时间步预测得到的概率分布,在下一个时间步内生成一个新的字母。
2.2计算损失
2.2.1问题
如果训练的序列很长,那么计算梯度的时就会很耗时。前向传播计算一次,反向传播再计算一次所有的序列。
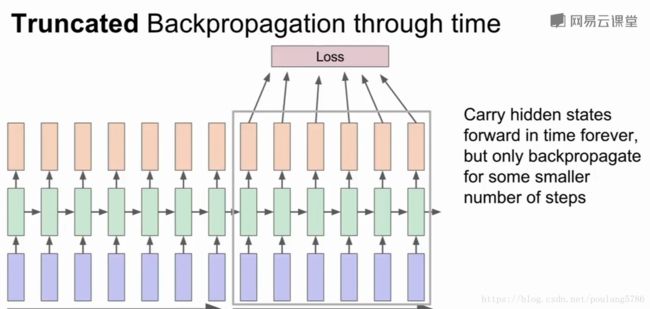
2.2.2沿时间截断的反向传播
我们每次只训练一部分序列,例如向前计算100步,然后只计算这100步子序列的损失,然后沿着100步反向计算梯度。
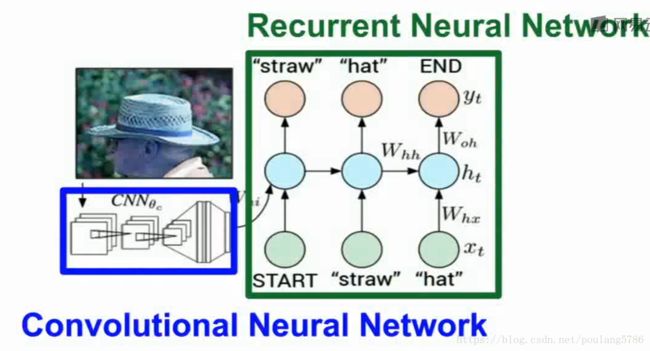
三.图像标注
图像标注就是输入图片,输出图片的语义信息。
有一部分卷积神经网络,处理输入的图像信息,在卷积网络训练完以后产生图像的特征向量。接下来特征向量输入到循环神经网络语言模型的第一个时序。
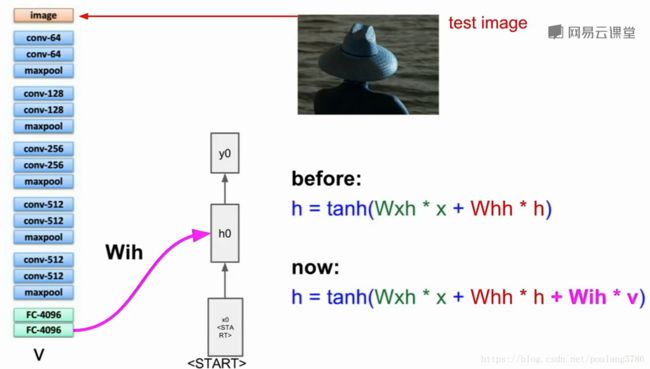
将图片输入后,使用模型输出的4096维的向量(ImageNet上训练)。用这个向量来概述整个图像的内容。使用递归神经网络的语言模型时需要模型的第一个初始化输入。
在之前的模型中,我们得到当前时间步的输入,以及前一个时间步的隐藏状态,结合之后得到下一个时间步的隐藏状态。但是现在我们需要添加图片信息,我们采用一个简单的方式就是加入第三个权重矩阵。在每个时间步中添加图像信息,来计算下一个隐藏状态。
接下来计算词汇表中所有分数的分布,从分布中采样,并在下一次时间步时当做输入传回,即在下一个时间步中输入传回的单词,然后得到一个关于所有词汇的分布,再取样产生下一个词。
上述事情做完后我们可以得到一个完整的句子。一旦采样到停止标记,就停止生成。
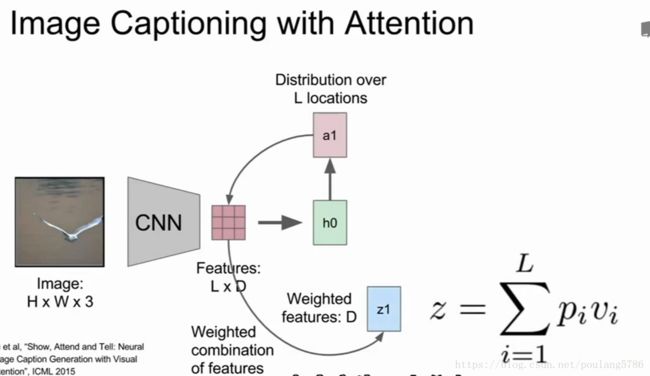
四.注意力模型
产生向量构成的网络,每个图片中特殊的地方都用一个向量来表示。
模型前向运行时,除了在每一步采样,也会产生一个分布,即图像中它想要看到的位置,图像位置的分布可以看做模型在训练过程中应该关注哪里的张量。
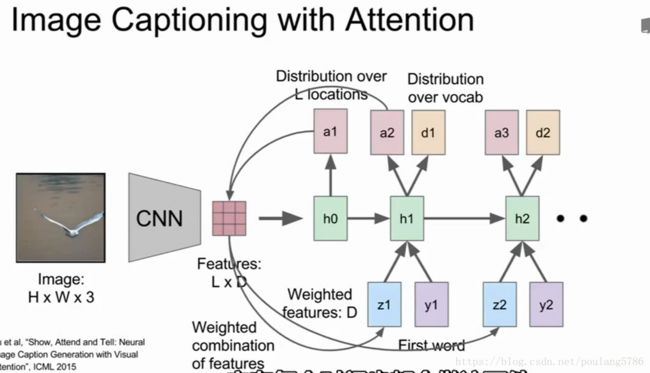
第一个隐藏态计算在图片位置上的分布,它将回到向量集合给出一个概要矢量,把注意力集中到图像的一部分上。
概要向量作为下一个时间步的额外输入,它会产生两个输出,一个是在词汇表的分布,另一个是图像位置的分布。继续下去,每一步都会做这两件事。
可以看到当生成一个描述时模型的注意力在图像的不同区域变换。
软注意力采用加权组合所有图像位置中的所有特征,硬注意力中我们限制模型在每一步只选择一个位置来观察图片。
五.视觉回答
模型有两个输入:一图片,二自然语言描述的问题,针对该图像进行的提问。
模型可以看做是CNN和RNN的结合。
RNN:
这是多对一的情形,模型将自然语言序列作为输入,针对输入问题的每个元素都建立递归神经网络,将输入问题概括为一个向量。
CNN:
CNN将输入图像概括为一个向量。CNN和RNN的向量结合(图像向量和输入问题的向量结合),通过RNN来预测答案的概率分布。
在右边我们可以看到,有时这个问题会和软注意力结合,模型在试图确定答案时会尝试确定感兴趣区域。
问题:1,如何将图像编码向量和问题描述向量结合:最常见的是将他们连接起来放入全连接层,两一种方法是让两个向量做乘法。
六.梯度消失和梯度爆炸
6.1多层递归神经网络
单层递归神经网络只有一个隐藏态,下面介绍多层递归神经网络。
一个三层的递归神经网络,第一层网络中产生了一系列隐藏态,第一层的隐藏态作为下一层的输入序列。
一般会使用二到三层的RNN,不会使用特别深的RNN。
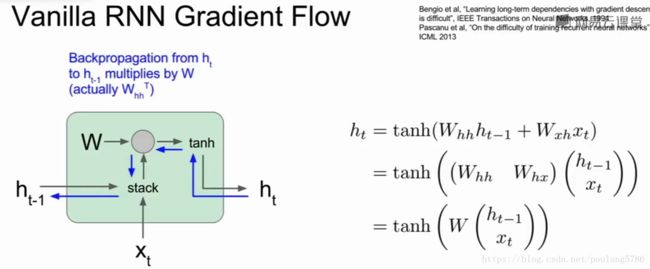
6.2Vanilla递归神经网络单元
xt作为当前时间步的输入,输入前一个隐藏态h(t-1),两个堆叠起来与权重矩阵做乘法,得到一个输出,将输出送入tanh激活函数,得到下一个隐藏状态。
反向传播过程中我们会得到ht的导数,以及关于ht损失函数的导数,反向传播通过这个单元时,我们需要计算关于h(t-1)损失函数的导数。
当计算反向传播时,梯度沿着红色线反向流动。梯度反向流过tanh门,反向流过矩阵乘法门,
我们把许多这样的单元连接成一个序列,梯度流穿过一系列这样的层。
计算h0损失函数的梯度,反向传播需要经过递归神经网络中的每一个单元,每次经过一个单元都要与其中w的转置做运算,意味着最终的表达式将会包含很多权重矩阵因子。
考虑标量形式,不断做乘法,会发生梯度爆炸或者梯度消失。
考虑矩阵时,矩阵的最大奇异值大于1,权重矩阵一个个相乘,h0的梯度将会非常大;最大奇异值小于1,发生梯度消失。
解决方法:
1.梯度爆炸:计算梯度后,如果L2的范式大于某个阈值,就将它剪断做除法,这样梯度就有最大阈值。(在训练循环神经网络时这样做比较有效,处理梯度爆炸)。
2.梯度消失:换一种更为复杂的RNN结构(LSTM网络)。
6.3 LSTM
长短期记忆网络,递归神经网络一种更高级的递归结构,LSTM用来缓解梯度消失和梯度爆炸。设计更好的结构来获取更好的梯度流动。
Vanilla中有隐藏态,每个时间步都更新隐藏态。
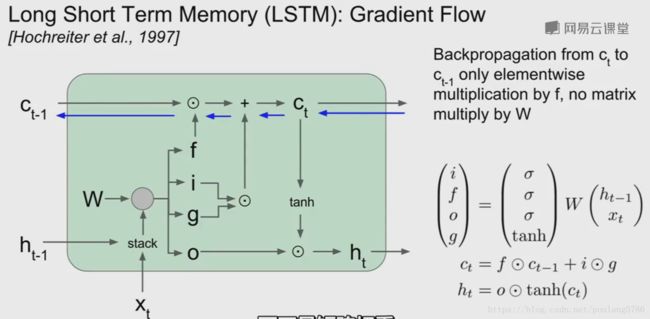
LSTM在每个时间步都维持两个隐藏态,一个是ht,叫做隐藏态(可以类比vanilla中的隐藏态),第二个是ct,单元状态,相当于保留在LSTM内部的隐藏状态。
看LSTM的更新公式,用两个输入来计算四个门,i,f,o,g,使用这些门来更新 单元状态ct,然后将这些单元状态(作为参数),来计算下一个时间步中的隐藏状态。
LSTM做的第一件事给定前一时刻的隐藏状态ht,和当前时刻的输入向量xt,在Vanilla中将ht和xt拼接然后进行矩阵相乘,计算得到RNN的下一个时刻的隐藏状态。在LSTM中,仍然拿到上一时刻的隐藏态和当前输入堆叠在一起,乘一个非常大的权重矩阵w,计算得到四个不同的门向量,每个门向量的大小和隐藏态都一样。
i代表input,输入门,表示LSTM要接受多少新的输入信息;f是forget,表示要遗忘多少之前的单元记忆,就是上一时间步的记忆信息;o是输出门,表示我们要展现多少信息给外部,g表示我们有多少信息要写到输入单元去。
他们用了不同的非线性函数,i,f,o都用了sigmod函数,意味着输出值在0和1之间,g用了tanh函数,输出在-1到1之间。
上一时间步的单元状态经过了f门的逐个元素乘操作,这个f门可以看做是0和1的向量,这些值告诉我们对于单元状态中的每个元素,如果f门中的元素是0,说明我们想要忘记这个单元状态中的元素值,如果f门中的元素是1,说明我们想要记住单元状态中的值。
当我们用f门来断开部分单元状态的值,我们就需要输入门i和g做逐个元素的乘法。i是由0和1构成的向量,i==1说明我们想要保留单元状态的那个元素,i==0说明不想保留单元状态对应的元素。
g门经过tanh后的值的范围是-1到1,这些值是当前时间步中我们可能会写入到单元状态中去的候选值。
单元状态的公式,每个时间步中单元状态都有不同的独立的标量值,在每个时间步中可以被加一或者减一,就是说在单元状态的内部我们可以保留或者遗忘之前的状态,在每个时间步中我们可以给单元状态的每个元素加上或减去最多为1的值。单元状态的每个元素可看做最小的标量计数器,每个时间步只能自增或自减。在计算了单元状态ct之后,我们将通过更新过的单元状态来计算隐藏态ht,这个向量要暴露到外部。
之前把单元状态解释成计数器,每个时间步都是加一或减一,我们把这个计数器用tanh压缩到0到1之间,现在用这个输出门逐个元素乘上单元状态,这个输出门是经过sigmod函数后的结果,所以它的组成元素大部分是0和1,输出门告诉我们对于单元状态中的每个元素我们在每个时刻计算外部的隐藏态时,到底想不想暴露那个单元状态的元素。
问题:
图中的权重矩阵W的来源:如果x和h的维度都是h,那么堆叠在一起就是尺寸为2h的向量,现在我们的权重矩阵大小是4h*2h,可以认为权重矩阵有四块不同的内容,权重矩阵的每块内容都分别计算其中的一个门。
LSTM内部发生了什么:
上一时间步的隐藏状态和当前时间步的输入堆叠在一起,然后乘以权重矩阵w来得到四个门(这里省略了非线性函数)。
f门和上一个时间步的单元状态做逐元素乘法;
i门和g门也做逐个元素的乘法然后加在一起,就得到下一个时间步的单元状态,下一时间步的单元经过一个tanh函数的压缩,由经过输出门(o门)的逐元素乘法,得到了下一时间步的隐藏状态。
在原始的循环神经网络中,在反向传播中我们不断乘以权重矩阵w,会发生梯度爆炸或消失。
但是在LSTM中,我们通过传输进来的单元获得了上游梯度,然后我们通过加法运算向后进行反向传播,这个加法运算仅仅是将上游梯度复制到这两个分支里,上游梯度可以直接被复制,并且通过元素相乘的方式直接贯穿了反向传播过程。上游的梯度最终通过f门得到相乘后的元素。
当我们通过这个单元状态向后反向传播时,对于上游的单元状态梯度唯一会发生的事情,就是最终他会通过f门得到相乘后的元素。
LSTM结构的优点:
1. f门是矩阵元素相乘,不是矩阵相乘
2. 矩阵元素相乘可能会在不同的时间点乘以一个不同的遗忘门(在Vaniila中我们不断乘以相同的权重矩阵)
3. f门是一个sigmoid函数矩阵元素相乘后的结果会保证在0到1之间。
在原始循环神经网络,反向传播过程中,在每一个梯度传播的时间步中都会经过一个tanh激活函数。而在LSTM中从最后一个隐藏态到第一个隐藏态只通过一个单一的非线性tanh向后传播,而不是在每一个时间步中单独设置tanh函数。
通过单元状态进行的反向传播路径,可以高速从模型末端返回单元的原始状态。
w的梯度传播,在每一个时间步中获得当前的单元状态及当前的隐藏状态,获得这个时间点的w局部梯度。将这些第一个时间步长w的梯度相加,计算出w的最后梯度。现在是一个很长的序列,只得到序列末端的序列,然后进行反向传播,会得到每一个时间步长w的局部梯度,这个w的局部梯度会经过c和h的梯度,在LSTM中很好的保留了c的梯度,所以在每一个时间步长的w的局部梯度也会随着时间的传播平稳地向前向后传播。
LSTM跟残差网络非常类似。