【LeetCode】91. Decode Ways
91. Decode Ways
Description:
A message containing letters from
A-Zis being encoded to numbers using the following mapping:'A' -> 1 'B' -> 2 ... 'Z' -> 26Given a non-empty string containing only digits, determine the total number of ways to decode it.
Example 1:
Input: "12" Output: 2 Explanation: It could be decoded as "AB" (1 2) or "L" (12).
Example 2:
Input: "226" Output: 3 Explanation: It could be decoded as "BZ" (2 26), "VF" (22 6), or "BBF" (2 2 6).
解题思路:
(1)递归解法
题目分析:
如果要用递归解法,就需要先找出递归公式:
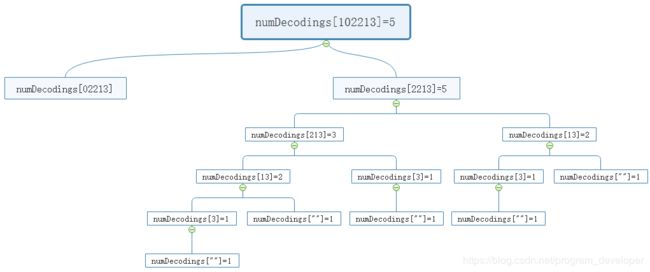
numDecodings[102213] = numDecodings[02213] + numDecodings[2213]
字符串“102213”解码的方式有两种:第一种,先解码子串“1”,再解码子串“02213”。但是以0开始的子串是无法解析的。第二种,先解码子串“10”,再解码子串“2213”。
解码子串“2213”也有两种方式:第一种,先解码子串“2”,再解码子串“213”。第二种,先解码子串“22”,再解码子串“13”。
以此类推。。。
规律显而易见,类似斐波那契数列。不同的是字符串从后往前推出递推公式。
递归公式:
numDecodings[s]= numDecodings[s.substring(1)] + numDecodings[s.substring(2)]
递归结束条件:
1. 当前指针所指字符为0
此时此字符无法解码,所以递归公式中的前者就只能为0,后者也为0。
例如【023】,substring(1)——【0】|【23】,截掉的【0】不能解析,所以此组合无效。
substring(2)——【02】|【3】,截掉的【02】不能解析,所以此组合无效。
所以0数字出现后,解码数的增量为0。
2. 当前字符的值是有效的(大于0),但是当前字符与右边字符组合的数字无效(大于26)。
相当于递归公式中的后者为0。
例如【3212】,substring(1)——【3】|【212】,截掉的【3】能解析,所以其值为【212】的解码数。
substring(2)——【32】|【12】,截掉的【32】不能解析,所以此组合无效。
递归代码:
不能AC,Time Limit Exceeded。
public class DecodeWays_91 {
public static void main(String[] args) {
// TODO Auto-generated method stub
String s = "102213";
System.out.println(numDecodings(s));
}
public static int numDecodings(String s) {
if(s.isEmpty())
return 1;
if(s.charAt(0) == '0')
return 0;
if(s.length() == 1)
return 1;
int res = numDecodings(s.substring(1));
if(s.charAt(0) == '1' || s.charAt(0) == '2' && s.charAt(0+1) - '0' <= 6 )
res += numDecodings(s.substring(2));
return res;
}
}(2)记忆化递归解法
由于递归解法包含很多重复的计算,我们把重复计算的结果先保存起来,等到用的时候,直接取出来。
已经AC代码:
import java.util.HashMap;
public class DecodeWays_91 {
public static void main(String[] args) {
// TODO Auto-generated method stub
String s = "102213";
System.out.println(numDecodings1(s));
}
public static HashMap memo;
public static int numDecodings1(String s) {
memo = new HashMap<>();
memo.put(null, 1);
return ways(s);
}
public static int ways(String s) {
if(memo.containsKey(s))
return memo.get(s);
if(s.isEmpty())
return 1;
if(s.charAt(0) == '0')
return 0;
if(s.length() == 1)
return 1;
int res = ways(s.substring(1));
if(s.charAt(0) == '1' || s.charAt(0) == '2' && s.charAt(0+1) - '0' <= 6 )
res += ways(s.substring(2));
memo.put(s, res);
return res;
}
}
(3)动态规划解法
1. 从递归的解法中,我们发现了重叠子问题。根据重叠子问题,我们得到最优子结构。
假设数组dp[i]表示从头到字符串的第i位,一共有多少种解码方法的话。那么如果字符串的第i-1位和第i位能组成一个10到26的数字,说明我们是在第i-2位的解码方法上继续解码,此时dp[i] = dp[i-2]。如果字符串的第i-1位和第i位不能组成有效二位数字,而且第i位不是0的话,说明我们是在第i-1位的解码方法上继续解码,此时dp[i] = dp[i - 1]。所以,如果两个条件都符合,则dp[i] = dp[i - 1] + dp[i - 2]。
2. 根据最优子结构,写出状态转移方程。
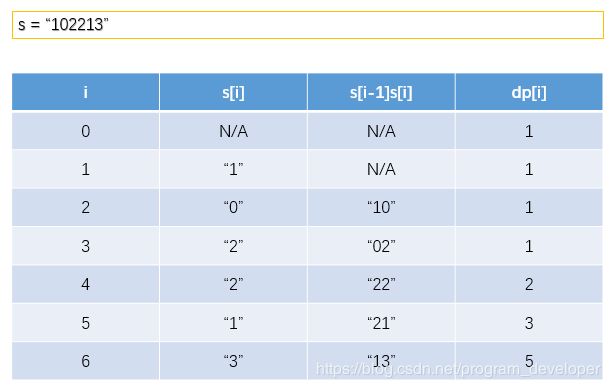
dp[i]的取值有以下四种情况:
1. 如果s[i]和s[i - 1]s[i]都是无效的话,dp[i] = 0;
2. 如果s[i]和s[i - 1]s[i]都是有效的话,dp[i] = dp[i - 1] + dp[i - 2] ;
3. 如果s[i]是有效的,s[i - 1]s[i]是无效的话,dp[i] = dp[i - 1];
4. 如果s[i - 1]s[i]是有效的,s[i]是无效的话,dp[i] = dp[i - 2];
- 如果 s[i] != '0',则 s[i]是有效的。
- 如果‘10’<= s[i - 1]s[i] <='26',则s[i-1]s[i]是有效的。
已经AC的代码:
public class DecodeWays_91 {
public static void main(String[] args) {
// TODO Auto-generated method stub
String s = "102213";
System.out.println(numDecodings(s));
System.out.println(s.substring(3-2, 3));
}
public static int numDecodings(String s) {
if(s.length() == 0)
return s.length();
int[] dp = new int[s.length() + 1];
//初始化第一种解码方式
dp[0] = 1;
//如果第一位是0,则无法解码
dp[1] = s.charAt(0) == '0' ? 0 : 1;
for(int i = 2; i <= s.length(); i++) {
// 如果字符串的第i-1位和第i位能组成一个10到26的数字,说明我们可以在第i-2位的解码方法上继续解码
if(Integer.parseInt(s.substring(i-2, i)) <= 26 && Integer.parseInt(s.substring(i-2, i)) >= 10) {
dp[i] += dp[i - 2];
}
// 如果字符串的第i-1位和第i位不能组成有效二位数字,在第i-1位的解码方法上继续解码
if(Integer.parseInt(s.substring(i-1, i)) != 0){
dp[i] += dp[i - 1];
}
}
return dp[s.length()];
}
}Reference:
【1】LeetCode第[91]题(Java):Decode Ways(解码方法数)
【2】花花酱 LeetCode 91. Decode Ways
【3】花花酱 LeetCode 91. Decode Ways 视频讲解
【4】[Leetcode] Decode Ways 解码方式