【LeetCode】300. Longest Increasing Subsequence
300. Longest Increasing Subsequence
Description：
Given an unsorted array of integers, find the length of longest increasing subsequence.
Example:
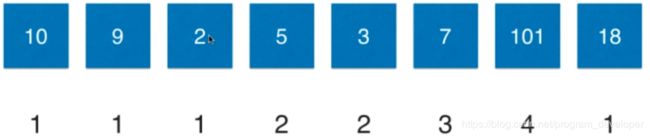
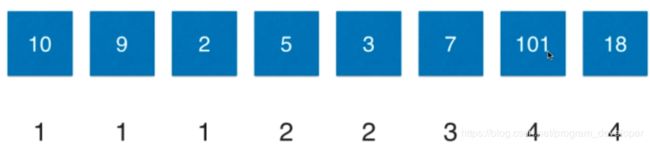
Input: [10,9,2,5,3,7,101,18] Output: 4 Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
Note:
- There may be more than one LIS combination, it is only necessary for you to return the length.
- Your algorithm should run in O(
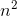) complexity.
Follow up: Could you improve it to O(n log n) time complexity?
题目中文解释：
（1）什么是子序列？
清楚题目中要求的子序列是：原序列中连续的子序列？还是原序列中可以间隔的子序列，这种序列可以保证元素相对位置不变。
（2）什么是上升？
这个问题关系到我们边界条件的考虑。前一个数大于后一个数这是绝对的上升，还有一种情况是前一个数和后一个数一样大，这也是上升。因此，我们需要根据题意考虑上升所带来的边界条件设定。
解题思路：
（1）暴力解题法：每一个元素放入序列中或者不放入两种情况。有n个元素就有O(
)个解法。
（2）动态规划解法
状态设定及状态转移方程：
举例说明：
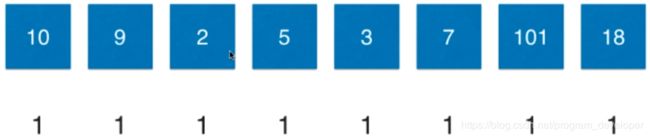
1. 对于一个序列，刚开始时都是含有一个元素的子序列。
2. 对于10来说，它的最长上升子序列就是它自己，所以长度为1。
对于9来说，它比10 小，它的最长上升子序列就是它自己，所以长度为1。
对于2来说，它比9 小，目前最长上升子序列是1；2在于10比较，2小于10，它的最长上升子序列就是它自己，所以长度为1。
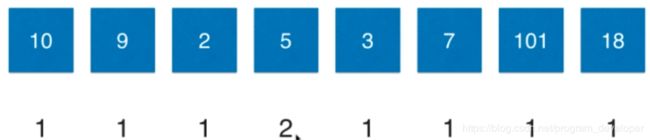
3. 对于5来说，前面的10和9比5大，无法构成上升子序列，长度为1。在比较2,5大于2，可以构成上升子序列，根据状态转移方程：LIS(3) = 1 + LIS(2) = 2。跟新数组如下：
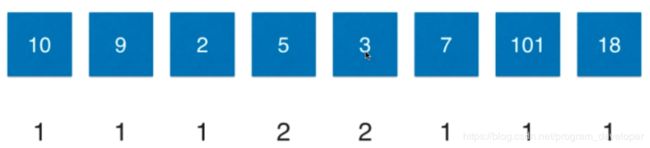
4. 对于3来说，3比10、9小，不能构成上升子序列。2可以放在3前面构成上升子序列，所以LIS(4) = 1+LIS(2)= 2。5不能放在3前面构成上升子序列，所以跟新数组如下：
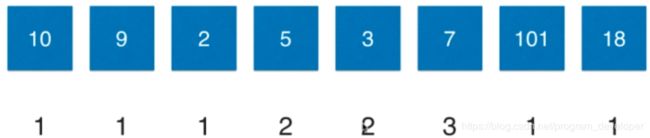
5. 对于7来说，10、9不能放在7前面所以不能构成上升子序列。
2可以，所以，LIS(5) = 1 + LIS(2) = 2。
5可以，所以，LIS(5) = 1 + LIS(3) = 3。
3可以，所以，LIS(5) = 1 + LIS(4) = 3。
选出能构成以7结尾的上升子序列的最大值为3。
6. 对于101，可以放在前面所有数字的后面，那么：
对于10来说，LIS(6) = 1 + LIS(0) = 2。
对于9来说，LIS(6) = 1 + LIS(1) = 2。
对于2来说，LIS(6) = 1 + LIS(2) = 2。
对于5来说，LIS(6) = 1 + LIS(3) = 3。
对于3来说，LIS(6) = 1 + LIS(4) = 3。
对于7来说，LIS(6) = 1 + LIS(5) = 4。
7. 对于18，可以放在它前面构成上升子序列的有：
对于10来说，LIS(7) = 1 + LIS(0) = 2。
对于9来说，LIS(7) = 1 + LIS(1) = 2。
对于2来说，LIS(7) = 1 + LIS(2) = 2。
对于5来说，LIS(7) = 1 + LIS(3) = 3。
对于3来说，LIS(7) = 1 + LIS(4) = 3。
对于7来说，LIS(7) = 1 + LIS(5) = 4。
8. 最终，扫描数组找出最大值即可。
在求解这个问题的过程中，我们有两个疑问：
（1）记录数组是不断升高的，我们求解最长上升子序列取记录数组中的最后一个值，是否可行？
（2）我们想要求当前数字所构成的最长上升子序列，是不是找到它前面与它最近且比它小的那个数字直接加1，不用再往前比较呢？
举例推翻上面两个疑问：
这个例子推翻上面两个疑问，即上面两个疑问都是错误的。
动态规划代码：
已经在LeetCode中AC。
class Solution:
def lengthOfLIS(self, nums):
'''
:param nums: List[int]
:return:
'''
if len(nums) == 0 :
return 0
memo = [1] * len(nums)
for i in range(1, len(nums)):
for j in range(i):
if nums[i] > nums[j]:
memo[i] = max(memo[i], 1 + memo[j])
res = 1
for i in range(len(nums)):
res = max(res, memo[i])
return res
solution = Solution()
nums = [10, 9, 2, 5, 3, 7, 101, 18]
print(solution.lengthOfLIS(nums))