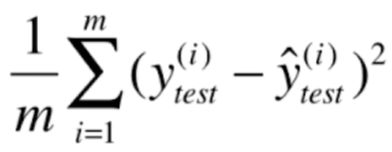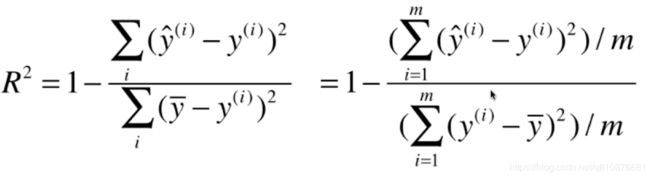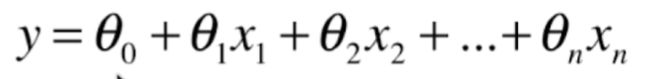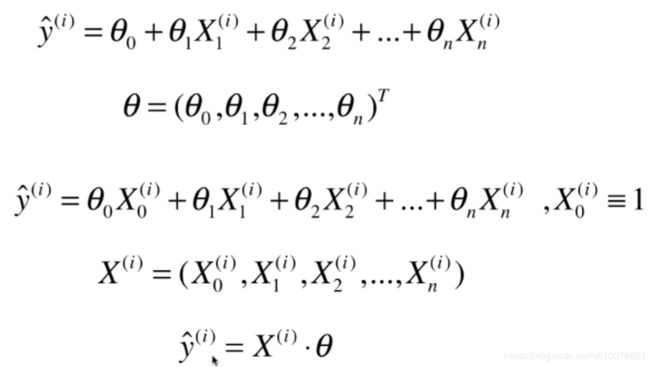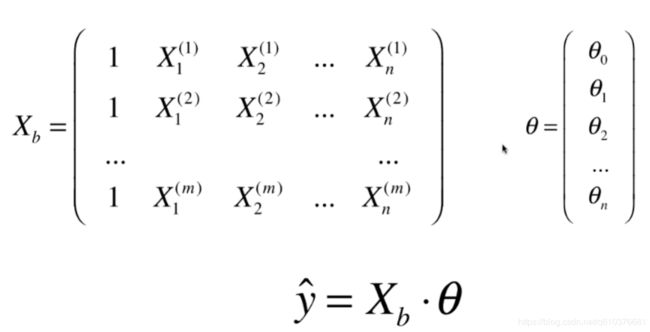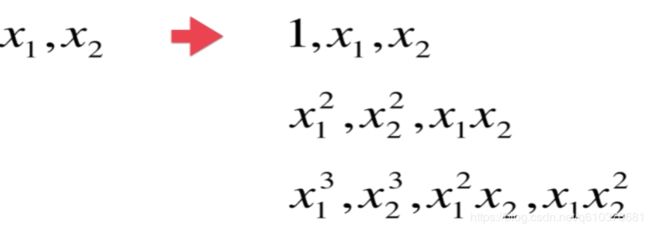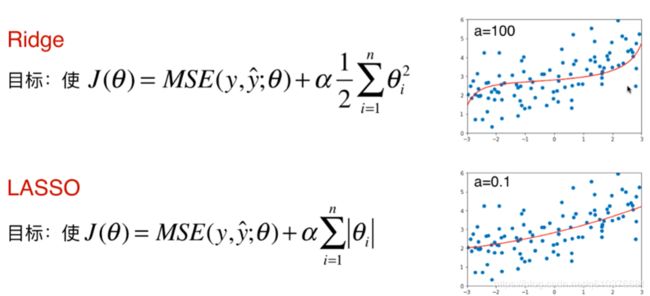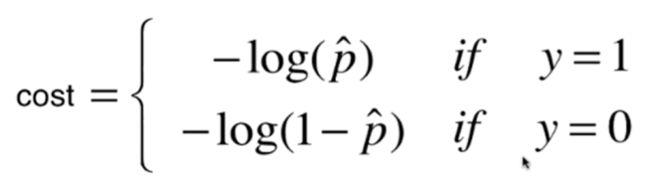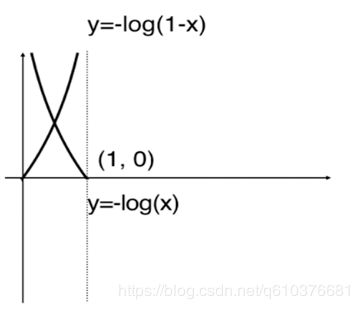机器学习算法入门(一)

前言:本课程是在慕课网上学习 Python3入门机器学习 经典算法与应用 课程时所做的笔记,供本人复习之用.学习这个的主要目的是为了应付这学期的机器学习选修课.所以只会大概讲解算法的意思,不会深入的进行实践或讲解原理.另外因为主要是供本人复习以及不打算仔细学,所以不保证写的一定对,只提供一个基本的理解.

目录

第一章 机器学习基础

1.1关于数据

1.2 机器学习的主要任务

1.2.1 分类任务

1.2.2 回归任务

1.3 什么是机器学习

1.4 监督学习,非监督学习,半监督学习和增强学习

1.4.1 监督学习

1.4.2 非监督学习

1.4.3 半监督学习

1.4.4 增强学习

1.5 批量学习,在线学习,参数学习,非参数学习

1.5.1 批量学习(Batch Learning)

1.5.2 在线学习(Online Learing)

1.5.3 参数学习(parametric Learning)

1.5.4 非参数学习(Nonparametric Learning)

1.6 和机器学习相关的哲学思考

1.6.1 数据的重要性

1.6.2 算法的选择

1.6.3 其它思考

第二章 k近邻算法 kNN

第三章 线性回归法

3.1 简单线性回归

3.2 衡量线性回归方法的指标

3.2.1 MSE

3.2.2 RMSE

3.2.3 MAE

3.2.4 R Squared

3.3 多元线性回归

第四章 梯度下降法(Gradient Descent)

4.1 线性回归中的梯度下降法

第五章 多项式回归

5.1 自己实现多项回归 

5.2 过拟合和欠拟合

5.3 模型的正则化

第六章 逻辑回归

6.1 逻辑回归的损失函数

6.2 逻辑回归的决策边界

6.3 逻辑回归的正则化

---

 

第一章 机器学习基础

1.1关于数据

我们使用著名的鸢尾花数据来说明,在这里有三个不同种类的鸢尾花.

总共有150个鸢尾花的数据信息,每个数据信息包括四个方面的信息.分别是萼片的长度与宽度,花瓣的长度与宽度.

整个数据就可以表示成这个样子.种类中我们标识了几个数,因为在计算机中我们希望将它们数字化.

我们根据三行的数据集来阐述一下在机器学习领域和数据相关的基本概念.

• 我们完成一个机器学习的任务,手里肯定是有数据的,通常我们管这些数据的整体叫做数据集.
• 对于一个数据集,通常我们可以写成一个表格的形式,在表格中每一行数据称为一个样本.具体到鸢尾花的数据中,每一行数据其实就是一朵花的信息.包含这一朵花的萼片的长度宽度.那么这一朵花就是一个样本.
• 除了最后一列,每一列都表达了样本的一个特征.可以简单的把一个特征理解成一个属性.比如说萼片的长度是一个特征,萼片的宽度是另外一个特征.
• 对这个数据来说,除了最后一列,其余的部分都是在描述数据整体的特征,通常在机器学习任务中,我们管这一部分用X来表示,之所是X是因为通常这部分是一个矩阵,这个矩阵有多少行就说明有多少样本,有多少列就说明有多少个特征,通过我们把第i个样本写作,第i个样本第j个特征值
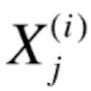
• 最后一列是特殊的一列,它是我们机器学习真正想去学的内容,称为标记.在表示上,我们通常用y来表示.第i个样本的标记写作
• 对于数据的每一行本身也组成了一个向量,通常我们管这个向量叫做特征向量,在数学中我们通常会把向量表示为列向量如图1,正因如此我们的矩阵可以写成图2所示 

                                                                   

                                               图1                                                                                     图2              

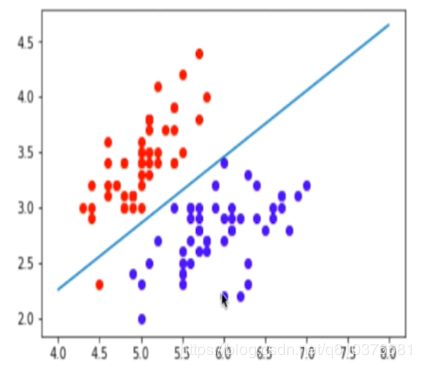
我们抽出数据的前两个特征,即萼片的长度与宽度,用萼片的长度作为横轴,萼片的宽度作为纵轴,可以想象,对于每一个样本来说,都会在横纵轴组成的坐标系中表示成一个点.当然这是为了我们可视化方便,所以我们选了两个轴在一个平面上来表示它.如果我们有3个维度就可以在三维空间中表示它,如果有四个维度就可以在四维空间中表示它,甚至有1000维度的话我们就可以在1000维空间中表示它,每一个样本的本质就是在这个空间中的一个点,这个空间我们称之为特征空间(feature space).

我们在下图中可以看出两类鸢尾花的特征分布是有极大的不同的,分类任务的本质就是在特征空间切分,不论低维还是高维空间.

这里花瓣的长度宽度都是有明确的语义的,即我们知道每一个数字代表什么意思,但是在机器学习领域中,特征可以是非常抽象的一个东西.举个例子对于图像识别来说,每一个像素点都是一个特征,对于28*28的图像有784个特征,换句话说,我们为了描述这个图像,我们可以使用784个数,每个数都代表着从左上角到右下角每一个像素点把它排开这个点对应的灰度值的深浅.然后利用这些特征来进行数字的识别.

如果是彩色图像特征更多.特征工程研究之一就是怎么喂给机器比较好的特征.

 

1.2 机器学习的主要任务

1.2.1 分类任务

比如判断一张图片是猫是狗,判断一个数字是0到9中的哪一个,分类任务就是将给定的任务进行分类.分类任务包括以下几种

二分类任务:

是猫是狗?是否是垃圾邮件?发给客户信用卡有没有风险?良性肿瘤恶性肿瘤?股票涨跌?

多分类任务:

数字识别,图像识别(猫狗鸟鳄鱼),信用卡风险评级(高中低)

很多复杂的问题也可以转化成多分类问题,比如玩2048时,是往上下左右哪个方向移动?下围棋的时候因为棋盘的大小是有限的,所以机器就是根据现在的棋盘信息选一个方向进行落子,甚至现在大红大紫的无人车,我们可以将它转换成方向盘向左向右打多少度,油门分成几个程度,具体踩多深等等.

当然这些问题是可以转换成多分类问题,但不一定使用多分类来解决这些问题是最好的.

后续的学习过程中,我们会了解到:

多标签分类:

之前的图片是放在一个类别中进行分类,比较高级的机器学习系统能放在多个类别中进行比较.这是比较前沿的话题.

 

1.2.2 回归任务

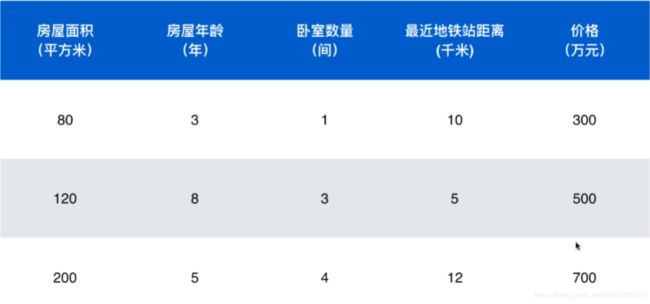
我们之前的标签列都是一个类别,但是在这个数据中,我们最终是一个价格.价格不是一个类别是一个连续的数字,这一类任务就是机器学习可以处理的另外一类任务了,叫做回归任务.

比如房屋价格,市场分析,学生成绩,股票价格.

 

 一些情况下,回归任务可以简化成分类任务,比如刚才提到的无人驾驶.方向盘打的角度是一个连续的数值,只不过我们将每一度看作一个类别.我们就将回归任务简化成了分类任务.

1.3 什么是机器学习

大量的学习资料就是数据集,我们将数据集喂给我们的机器学习算法,我们的机器学习算法将根据我们的数据集训练一个模型,当有了新的样本资料以后,是通过这个模型来得到输出结果的.这个输出结果有两类,一个是样本的类别,另外一类是具体的数值.

我们的模型其实就是一个函数,这里我们的函数需要的每一个小的x就是一个样本资料.我们机器学习算法本质是获得一个新的f(x).这样当我们有新的样本资料x时,只要把它送给我们训练好的f(x),这个f(x)就会根据它的函数规则得到一个结果.如果结果时0,1,2,3,4这样的类别的话,我们解决的就是一个分类问题,如果f(x)得到的是一个具体的数值的话,我们解决的就是一个回归问题.

上面我们说了分类和回归问题,其实是监督学习主要解决的是分类和回归问题,机器学习还可以解决很多其它的问题.

 

 

1.4 监督学习,非监督学习,半监督学习和增强学习

我们之前是根据能机器学习能解决的问题进行了分类,现在我们将根据机器学习的算法进行分类.

1.4.1 监督学习

给机器的训练数据拥有标记或者答案.

监督学习算法:

k临近,线性回归和多项式回归,逻辑回归,SVM,决策树和随机森林.

1.4.2 非监督学习

很多时候非监督学习是辅助监督学习的运行.

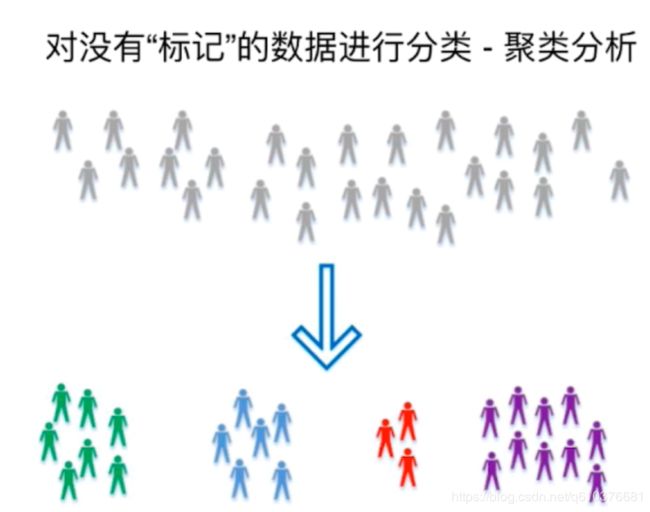
给机器的的训练数据是没有任何"标记"或者答案.

非监督学习可以完成分类任务.

比如电商网站上的人群分类,某些人是理智型消费者,有些人是冲动型,有些人更在乎性价比等等...

非监督学习可以对数据进行降维处理和异常检测.

降维处理包含两部分内容,特征提取和特征压缩.

特征提取:当我面对一个数据时,这个数据有很多特征,有时候根据经验或深入分析,认为某一些特征对我们预测或者计算的结果是没有贡献的,比如银行需要用收集的个人信息对个人信用进行评级,而个人的胖瘦与信用评级是没有关系的,这叫做特征提取.

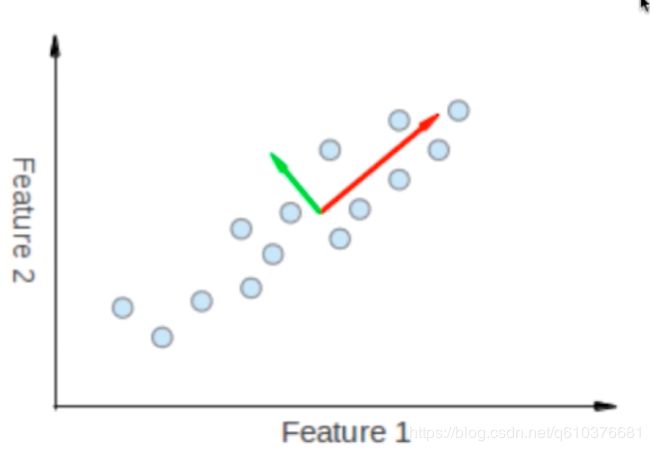
特征压缩:PCA,我们并不扔掉任何特征,下图是一个二维的特征平面,这个二维的特征平面上分布很多的数据点,但这些点是呈直线的形式,如果我们画一根直线的话,把所有的点都映射在倾斜的直线上,那么这些点的直线信息并没有丢失多少,但是经过这样的处理后,二维的点就变成了一维的点.

之前我们说28*28的图片要784个特征,经过特征压缩后,只需要十几个特征就行了.

降维处理的意义:方便可视化.对于人类来说是无法理解四维以上的信息的,有的时候我们可以把很高维的数据降到三维甚至二维,降到这么低的维度可能已经丢失了很多信息,我们降到这么低的维度主要是为了对信息进行可视化.

异常检测:有时候在我们的数据中存在一些点,这些点是存在异常的,这种点对于让我们的算法发现一般性规律是没有帮助的,对于二维的我们可以肉眼看到,对于高维的我们就需要用非监督学习算法剔除这些点.

 

1.4.3 半监督学习

一部分数据有"标记"或者"答案",另一部分数据没有.因为在实际生活种会因各种原因产生数据的缺失.

通常是使用无监督学习手段对数据做处理,之后使用监督学习手段做模型的训练和预测.

 

1.4.4 增强学习

我们机器学习的算法通常叫做agent,我们机器学习的算法要根据周围的环境来采取行动,在采取去了行动之后,我们的算法就会收到一些反馈,这个返回有时候是使用reward,有时候是使用state机制来进行反馈,agent算法得到了反馈之后就会改进自己的行为模式,之后在面对环境的其它的情况下,根据改进的算法再做出相应的action.然后环境再反馈给我们的agent.依此类推,可以看出我们的agent在一轮一轮的行动反馈中逐渐增强自己的智能.所以称之为增强学习.

前沿领域的无人驾驶与机器人都需要增强学习.

监督学习与半监督学习是基础.

 

1.5 批量学习,在线学习,参数学习,非参数学习

1.5.1 批量学习(Batch Learning)

批量学习就是收集一定量的样本资料,送给我们的机器学习算法,我们的机器学习算法就可以训练出一个模型,当我们训练出这个模型后就可以直接投入到生产环境中了.在具体应用的时候可能又有新的样例送进来,通过我们的模型来预测出相应的结果.这个过程中我们的模型不会再发生变化了.

优点:简单

问题:

如何适应环境变化?如垃圾邮件,每年都会有新的种类的垃圾邮件

解决方案:定时重新批量学习,运算量巨大.

缺点:每次重新批量学习,运算量巨大.在某些环境变化非常快的情况下,甚至是不可能的.如股市.

1.5.2 在线学习(Online Learing)

在线学习就是每次我们输入样例到模型得到输出结果之后,我们的输入样例并不浪费掉,有时我们会很快拿到输入样例的正确结果,如对股市进行预测,我们很快就能拿到样例的真实结果,我们拿真实结果和预测结果进行比较,这些信息仍然是机器学习算法需要的学习资料.我们可以将这些信息迭代进机器学习算法.改进我们的模型,以此类推,这个过程不断地循环,相当于在线的过程不仅是应用模型得到我们想要的结果,与此同时我们还再不断训练我们的模型,进行学习.

优点:及时反映新的环境的变化

问题:

有些不正常的新的数据带来不好的变化.

解决方案:需要加强对数据进行监控.

其它:有时也适用于数据量巨大,无法完全批量学习的环境.

 

1.5.3 参数学习(parametric Learning)

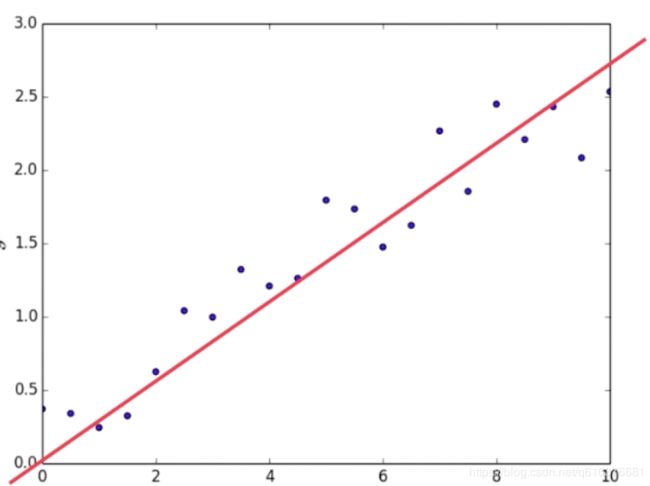
如下图所示,横坐标是房屋的面积,纵坐标是房屋的价格,对应每一个房屋在这个特征空间中就有一个点,基于这些数据点我们可以假设房屋的价格之间是一个线性的关系,即我们假设房租的价格是f(x)=a*x+b,当我们拥有了这个假设之后,我们整个机器学习的过程就是找到合适的a和b来描述房屋的面积和价格之间的关系.a和b就是参数.基于这样的学习特点,相应的机器学习算法就叫做参数学习,那么我们刚才描述的学习的方法就是最为基础的线程回归机器学习方法.

刚才我们预测是线性关系,事实上我们可以做出非常多的假设,在统计学领域有非常多的统计模型,我们可以假设我们的特征和要预测的结果之间是某种统计模型可以涵盖的,之后我们的任务就是学习统计模型中的参数.一旦学习到了这些参数之后,我们的预测相对是非常简单的.不再需要原有数据集的参与.

 

1.5.4 非参数学习(Nonparametric Learning)

不对模型进行过多的假设,通常在预测的过程中,我们喂给算法的数据集也要参与进预测的过程中,要注意的是非参数不代表没有参数,在后续的学习中会发现,很多非参数学习里面的参数并不少.两个种类的主要区别就是不把整个问题进行一个建模,不把整个问题理解成是学习一些参数.但是在学习过程中依然是需要一些参数来参与的.

1.6 和机器学习相关的哲学思考

1.6.1 数据的重要性

2001年微软的一篇论文,这篇论文大意是指对于四个不同的机器学习算法,从算法的角度它们是有优有劣的,但是如果喂以足够多的数据,横坐标是数据的规模,所有算法的准确率都在稳定的上升,纵坐标是准确率.当数据大到一定程度后,算法的准确率相差并不多.

所以数据非常重要.

但是在2017年人工智能界有了新的突破,AlphaGo Zero不需要喂任何数据,所有数据都是由算法产生的,即使没有数据,也可以人工生成数据,当然围棋有它的特殊性,但是也说明了一些问题.

1.6.2 算法的选择

奥卡姆的剃刀原则:

简单的就是好的.对于一个问题,不要进行过多的假设,不要进行过多的复杂化.

可是容易引发争议的问题是,到底在机器学习领域中,什么叫"简单"?

在这里只是想说,机器学习处理的是不确定的世界中的真实的问题,对于很多问题来说,并没有标准的答案.

没有免费的午餐定理:

整个定理讲述的是,可以严格地数学推导出:任意两个算法,他们的期望性能是相同的.

既然任意算法的期望性能是相同的,那么我们为什么还要学习新的算法呢?

因为这里值得是期望,但是具体到某个特定特定的问题,有些算法可能更好.所以我们还是要真正的去寻找,在我们要解决的领域里,哪个算法更好.

但没有一种算法,绝对比另一种算法好.脱离具体问题,谈算法的好坏是没有意义的.

在面对一个具体的我呢提的时候,尝试使用多种算法进行对比实验,是很有必要的.

1.6.3 其它思考

面对不确定的世界,怎么看待使用机器学习进行预测的结果?比如美国的大选,有的团队预测对了,有的团队预测错了,那么预测对的到底是机器学习算法起到了重要作用还是仅仅是一个巧合?这同样也类似于预测股票经济历史等等.

还有预测根据人的长相预测人成为罪犯的概率,是否会得某种病的概率.我们该怎么看待这种预测结果.

这种思考甚至会产生出一门新的学科,机器伦理学.

第二章 k近邻算法 kNN

主要解决的是分类为题.

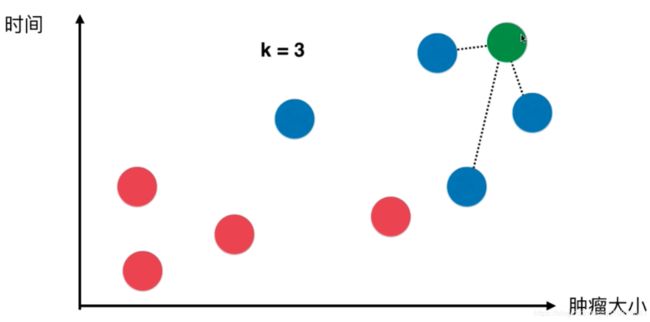
下图是肿瘤病人相关的数据,横轴代表一个特征是发现肿瘤病人肿块的大小,纵轴是发现肿块的时间.对于每一个病人,它的肿块大小和发现的时间都成为了特征平面中的一个点,对于这个点我们又知道了它是一个恶性的肿瘤还是一个良性的肿瘤,恶性肿瘤用蓝色来表示,良性肿瘤用红色来表示.这样如果新来了一个病人,用绿色的点表示,那么我们怎么知道他的肿瘤是良性的还是恶性的呢?

k临近算法是这样的,先选定一个k值,假设是3,对于每一个新的数据点,k近邻算法做的就是在所有的点中,寻找离这个点最近的三个点,如果最近的点蓝的多,那么这个点就是蓝的,红的亦然.这里蓝色比红色是3:0,所以这个肿瘤是恶性的.

 

第三章 线性回归法

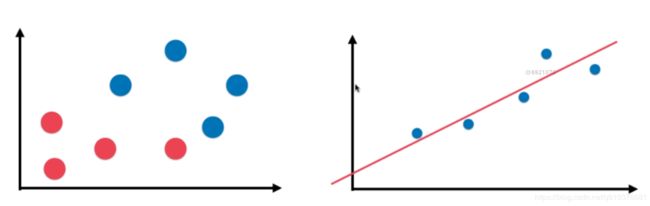
对于分类问题问题,我们上面讲的是横轴代表肿瘤大小,纵轴代表肿瘤时间,样本的输出标记是被样本是红色的点还是蓝色的点所表示的,蓝色的点代表是恶性的,红色的点代表是良性的.我们在这一小节举得例子中,只有横轴是样本的特征,纵轴就已经是样本的输出标记了也就是房租的价格,因为在回归问题中我们真正要预测的是一个具体的数值,这个具体的数值是在一个连续的空间中,而不是可以用简单的颜色来表示的,如果我们要想看有两个样本特征的回归问题,我们需要在三维空间中观察.在接下来的讲解中为了便于理解,我们对于线性回归这种可视化的讲解使用只有一个特征来讲解.

3.1 简单线性回归

对于样本的特征只有一个使用线性回归法进行预测,我们可以用简单线性回归来称呼它,简单线性回归,顾名思义,相对来说是比较简单的,我们可以通过对简单线性回归的学习推广到多个,样本特征有多个的话就叫多元线性回归.

下面是评估线性回归法性能的方法,因为绝对函数不可导,所以我们这里用平方的方法.

 

 

3.2 衡量线性回归方法的指标

对于一个数据集,我们把它分为训练数据和测试数据,在线性回归中,我们用我们的训练数据找出最好的a,b,用测试数据来测试a,b的好坏.

现在有两个训练出的a,b那么哪个比较好呢?

3.2.1 MSE

我们之前说的是将误差的平方和相加,但是可能一个是1000个样本数据误差的累加,一个是100的误差的累加,这样难以说明问题,所以我们取样本的平均值.

3.2.2 RMSE

我们之前用的是平方,但是这样有可能会有量纲的问题,比如误差是万元,那现在的误差是万元的平方.一个简单的优化方法是把MSE的值开一个平方.

3.2.3 MAE

之前在训练的过程中我们不用相减绝对值去求是因为绝对值不好求导,现在可以用它来评估误差.

3.2.4 R Squared

 RMSE与MAE还是有它们的问题,

当我们用房产数据进行预测的时候,用RMSE或MAE得到的数据是5万元,而我们预测学生的成绩,预测的最终结果是10分,那么这种情况就难以说明我们的算法是作用在预测房产上好,还是预测学生成绩上好.

这种情况是可以解决的,解决的方法是用一个新的指标R方.

看着比较麻烦,其实ssresidual就是预测结果减去真值平方和,sstotal就是平均结果减去真值的平方和.

另外:

                           

3.3 多元线性回归

和之前讲的简单线性回归类似,只是这里的特征变成了n个.

当有n个特征的时候,方程可以表示为如下,表示的就是b,表示的就是a.

预测值为如下:

求解的思路也和简单线性回归类似.主要是使损失函数尽量小

可变成一个列向量,X可以变成一个行向量,为了保持一致性这里我们加了一个X0.

上面只是一个样本的预测,我们可以把X推广到所有的样本上.这个Xb有m行n+1列.是一个列向量.y hat(带尖角的y)是一个列向量,是所有样本的预测值.

 

这样就能解出,但是时间复杂度过高.O(n^3)(优化O(n^2.4)),有更快的方法,如梯度下降法等.

 

第四章 梯度下降法(Gradient Descent)

梯度下降法不是一个机器学习算法,是一种基于搜索的最优化算法,作用是最小化一个损失函数.

我们的参数每次加上就能保证向损失函数减少的方向移动,这样一次次移动就能找到损失函数的最小值.比如在这里我们的导数是负值,乘上－,便会增大,损失函数就会减小.

这里是二维函数,对应的是导数,与x对应.如果是多维函数,对应的就是梯度.

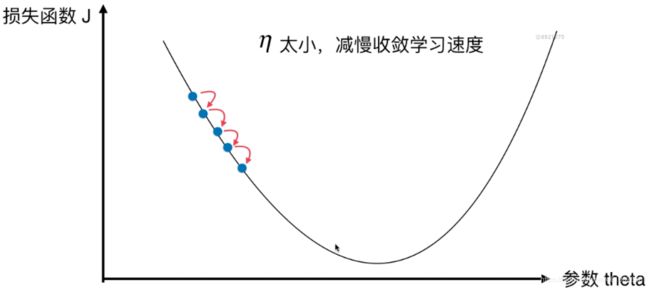
 成为学习率,的取值影响获得最优解的速度,取值不合适,甚至得不到最优解,是梯度下降法的一个超参数.

 

并不是所有函数都有唯一的极值点.

解决方案:

多次运行,随机化初始点,梯度下降法的初始点也是一个超参数.

 

4.1 线性回归中的梯度下降法

现在我们的样本特征变成了n个,之前是对一个求导,现在未知数多了,要对某个未知数求偏导.

 

 

我们希望我们求出来的值与m的个数是无关的,所以我们加上m分之一来消除m的影响.

按照上面这样就求出来对应的梯度J()了,然后根据每次向梯度的方向进行一定的移动,直到找到极值就行了.基本步骤和二维的差不多.

第五章 多项式回归

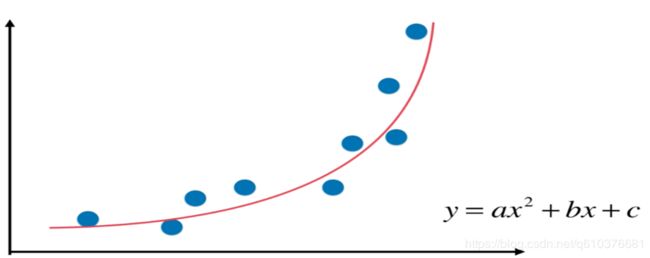
之前学习线性回归的时候,需要预测的是直线,有的数据需要曲线等等拟合.这样我们就需要多项式回归.我们可以把二次项看作另外一个特征.

5.1 自己实现多项回归 

添加一层x^2特征,然后利用原来的线性回归去做就行了.

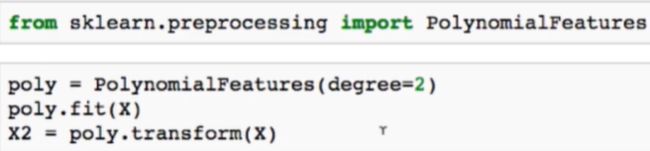
我们可以用sklearn来生成新的特征,degree表示我们要为原本的数据集添加几次幂这样的特征.如果添加2次的话,一个

[2.44,2.59,-1.34,-0.33,-2.33]的矩阵就变成下图所示.

值得注意的是sklearn不只是生成一个特征,而是生成多个,当degree为3,原本有x1,x2两个特征,用sklearn生成的特征如下.

5.2 过拟合和欠拟合

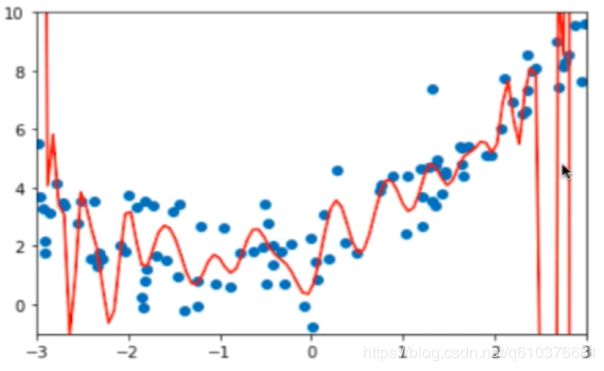
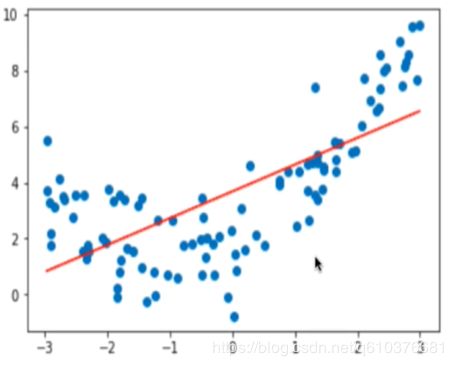
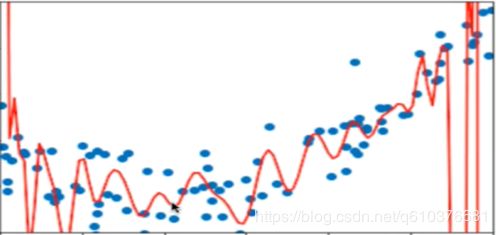
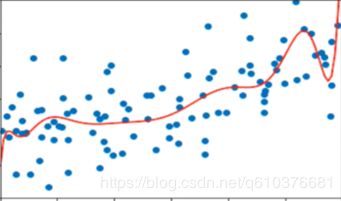
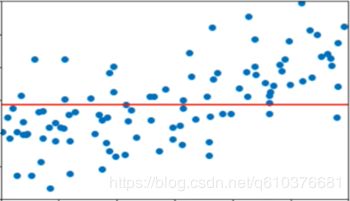
如上面所说,按degree的不同会生成不同的特征,如果degree过大,则预测的结果会过于拟合我们的测试数据集,如果过小,则会对测试数据集拟合结果不好.

过拟合

欠拟合

5.3 模型的正则化

机器学习的主要挑战,来自于方差.解决的方法有挺多,降低模型复杂度,减少数据维度,增加样本数,使用验证集等等,除了这些,解决高方差的一个主要手段就是模型正则化.

当我们过拟合时,模型的系数往往非常的大,下面是一个100次幂的系数.当系数过大时,就会越陡.如下左图是系数,可以看到有10^11次方出现.

                 

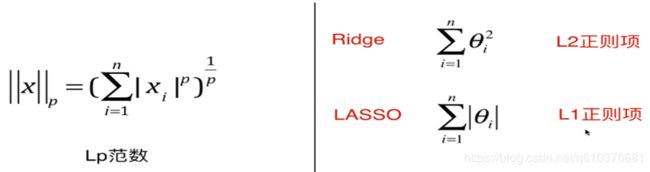
考虑到我们我们在计算结果的时候会使方差尽量小,我们又不希望过大,我们可以在方差中加入来进行平衡.下图我们在方差上加上了α ^2,这样我们计算方差的时候便不会过大.

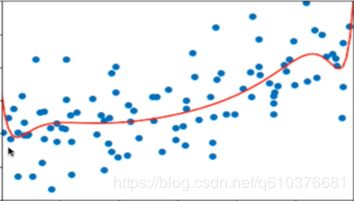
下图是随着α逐渐增大,函数图像的变化.

 

                                    

除了加上平方,还有一种方式.

 

第六章 逻辑回归

逻辑回归虽然是回归.但解决的却是分类问题.这里用了一个比较巧妙地函数将一个连续的值变成了0与1之间的值,我们还是通过刚才的方法预测值,只不过预测的值要带进sigmod函数中,可以看到sigmod函数的范围在(0,1)之间,所以我们将预测的带入后也将是一个(0,1)之间的值,所以可以作为概率预测.

                                                             

6.1 逻辑回归的损失函数

如果真值是1,那么我们预测的p越小,cost越大.

如果真值是0,那么我们预测的p越大,cost越大.

下面的两个函数可以实现上诉要求,既越接近0,cost越大,与越接近1,cost越大.

      

为了方便我们可以将上面两式子合成一个. 

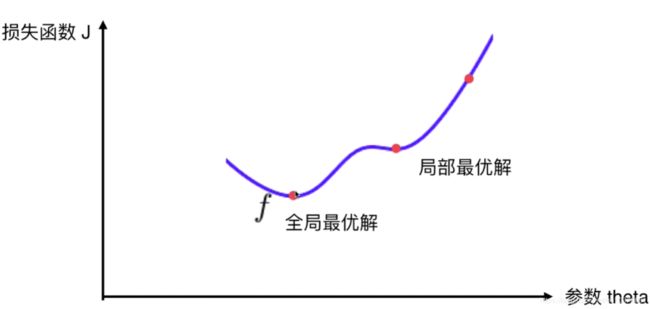
这个式子没有公式解,只能用梯度下降法求解.但这个损失函数是凸函数,没有局部最优解,只有全局最优解,所以不用担心求到的解不是最优解.

6.2 逻辑回归的决策边界

决策边界就是p等于二分之一,即 ^T * Xb =0 的X的取值.

如果有两个特征

                       

 

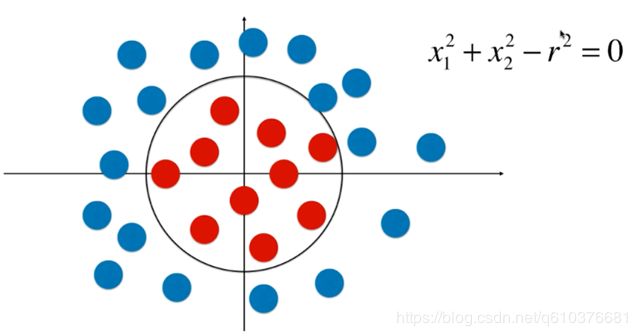
刚才的决策边界是直线,我们可以直接将特征带入公式去计算,但是如果边界是不规则的,如下面的圆形边界,我们就需要按照多项式回归那样,去自己构造特征.可以用sklearn去生成特征.

6.3 逻辑回归的正则化

这个我也不大懂,看看就好.