算法模型---树相关---决策树
决策树的特点
决策树的用途
决策树的适用范围
数据类型
特征可以连续和离散
因变量分类时是离散,回归时是连续
| 算法 | 支持模型 | 树结构 | 特征选择 | 连续值处理 | 缺失值处理 | 剪枝 |
|---|---|---|---|---|---|---|
| ID3 | 分类 | 多叉树 | 信息增益 | 不支持 | 不支持 | 不支持 |
| C4.5 | 分类 | 多叉树 | 信息增益比 | 支持 | 支持 | 支持 |
| CART | 分类,回归 | 二叉树 | 基尼系数,均方差 | 支持 | 支持 | 支持 |
决策树的优点
1)简单直观,生成的决策树很直观。
2)基本不需要预处理,不需要提前归一化,处理缺失值。
3)使用决策树预测的代价是O(log2m)。 m为样本数。
4)既可以处理离散值也可以处理连续值。很多算法只是专注于离散值或者连续值。
5)可以处理多维度输出的分类问题。
6)相比于神经网络之类的黑盒分类模型,决策树在逻辑上可以得到很好的解释
7)可以交叉验证的剪枝来选择模型,从而提高泛化能力。
8) 对于异常点的容错能力好,健壮性高。
决策树的局限性
1)决策树算法非常容易过拟合,导致泛化能力不强。可以通过设置节点最少样本数量和限制决策树深度来改进。
2)决策树会因为样本发生一点点的改动,就会导致树结构的剧烈改变。这个可以通过集成学习之类的方法解决。
3)寻找最优的决策树是一个NP难的问题,我们一般是通过启发式方法,容易陷入局部最优。可以通过集成学习之类的方法来改善。
4)有些比较复杂的关系,决策树很难学习,比如异或。这个就没有办法了,一般这种关系可以换神经网络分类方法来解决。
5)如果某些特征的样本比例过大,生成决策树容易偏向于这些特征。这个可以通过调节样本权重来改善。
基于决策树的分类
系列内容为自己学习数据挖掘的一个笔记
本部分内容来源《数据挖掘导论》4.3节
决策树生成算法
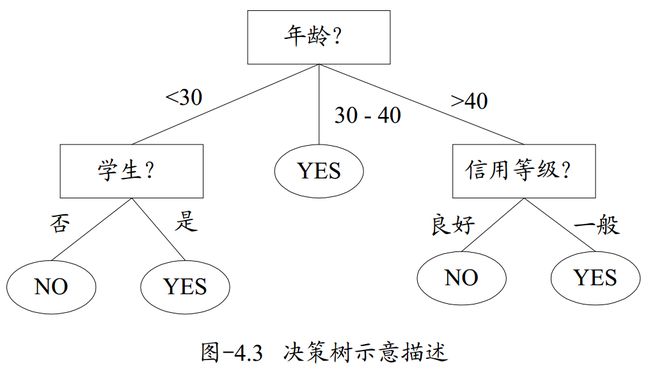
所谓决策树,就是一个类似于流程图的树形结构,树内部的每一个节点代表的是对一个特征的测试,树的分支代表该特征的每一个测试结果,而树的每一个叶子节点代表一个类别。树的最高层是就是根节点。下图即为一个决策树的示意描述,内部节点用矩形表示,叶子节点用椭圆表示。该决策树用于对一个顾客是否会在本商场购买电脑进行分类预测。
从根节点到叶节点的一条路径就形成对相应对象的类别预测,决策树很容易转换为分类规则。
算法4.1就是学习构造决策树的一个基本归纳算法。
决策树基础版本(ID3)的学习策略:
- 从根节点出发,根节点包括所有的训练样本。
- 一个节点(包括根节点),若节点内所有样本均属于同一类别,那么将该节点就成为叶节点,并将该节点标记为样本个数最多的类别。
- 否则利用采用信息增益法来选择用于对样本进行划分的特征,该特征即为测试特征,特征的每一个值都对应着从该节点产生的一个分支及被划分的一个子集。在决策树中,所有的特征均为符号值,即离散值。如果某个特征的值为连续值,那么需要先将其离散化。
- 递归上述划分子集及产生叶节点的过程,这样每一个子集都会产生一个决策(子)树,直到所有节点变成叶节点。
- 递归操作的停止条件就是:
(1)一个节点中所有的样本均为同一类别,那么产生叶节点
(2)没有特征可以用来对该节点样本进行划分,这里用attribute_list=null为表示。此时也强制产生叶节点,该节点的类别为样本个数最多的类别
(3)没有样本能满足剩余特征的取值,即test_attribute= 对应的样本为空。此时也强制产生叶节点,该节点的类别为样本个数最多的类别
对应的样本为空。此时也强制产生叶节点,该节点的类别为样本个数最多的类别
算法4.1://根据给定数据集产生一个决策树
输入: 训练样本,各特征值均取离散值,可供归纳的候选特征集为:attribute_list。
输出: 决策树。
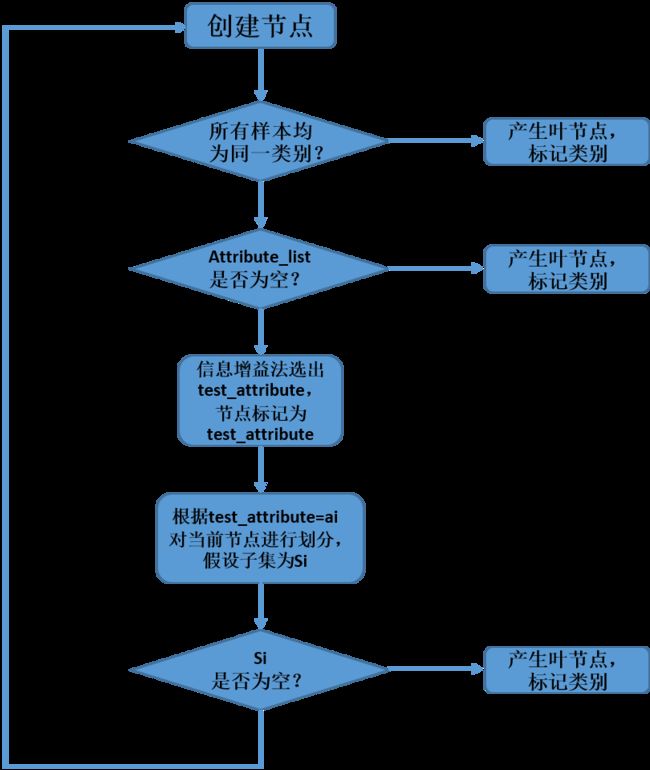
处理流程:
特征挑选方法(信息增益法)
选择具有最高信息增益的特征作为测试特征,利用该特征对节点样本进行划分子集,会使得各子集中不同类别样本的混合程度最低,在各子集中对样本划分所需的信息(熵)最少。
下面对信息增益法进行解释。
假设某节点S包含s个样本,共有m个类别,分别对应 C i , i ∈ { 1 , 2 , … , m } C_i,i\in \{1,2,\dots,m\} Ci,i∈{1,2,…,m},每一个类别中包含样本数为 s i s_i si,此时确定节点中任意一个样本的类别所需的信息量(信息熵)为:
I ( s 1 , s 2 , … , s m ) = − ∑ i = 1 m p i ∗ l o g ( p i ) I(s_1,s_2,\dots,s_m)=-\sum_{i=1}^{m} p_i * log(p_i) I(s1,s2,…,sm)=−i=1∑mpi∗log(pi)
其中, p i p_i pi为任一样本属于类别 C i C_i Ci的概率,因而有 p i = s i / s p_i=s_i/s pi=si/s。关于信息熵的定义可以查阅信息论的相关书籍。
假设特征A有v个不同取值, { a 1 , a 2 , . . . , a v } \{ a_1,a_2,...,a_v \} {a1,a2,...,av},那么利用特征A可以将该节点样本划分为v个子集 { S 1 , S 2 , . . . , S v } \{ S_1,S_2,...,S_v \} {S1,S2,...,Sv}, S j S_j Sj包含了集合S中特征A取 a j a_j aj值的样本集合,对应的样本数为 s j s_j sj。假设 S i j S_{ij} Sij为子集 S j S_j Sj中属于类别 C i C_i Ci的样本集合,对应的样本数目为 s i j s_{ij} sij,那么在子集 S j S_j Sj中确定任一样本类别所需的信息熵为:
I ( s 1 j , s 2 j , … , s m j ) = − ∑ i = 1 m p i j ∗ l o g ( p i j ) I(s_{1j},s_{2j},\dots,s_{mj})=-\sum_{i=1}^{m} p_{ij} * log(p_{ij}) I(s1j,s2j,…,smj)=−i=1∑mpij∗log(pij)
对所有子集中的样本进行类别确定所需的信息熵应为单独在各子集进行样本类别确定所需信息熵的的加权平均:
E ( A ) = ∑ j = 1 v s 1 j + s 2 j + . . . + s m j s ∗ I ( s 1 j , s 2 j , . . , s m j ) E(A)=\sum_{j=1}^{v} \frac{s_{1j }+s_{2j} +...+s_{mj} }{s} * I(s_{1j},s_{2j},..,s_{mj}) E(A)=j=1∑vss1j+s2j+...+smj∗I(s1j,s2j,..,smj)
上式中 s 1 j + s 2 j + . . . + s m j s \frac{s_{1j }+s_{2j} +...+s_{mj} }{s} ss1j+s2j+...+smj即为第j子集的权值。
这样利用特征A对当前节点的样本进行划分子集的信息增益为:
G a i n ( A ) = I ( s 1 , s 2 , . . . , s m ) − E ( A ) Gain(A)=I(s_1,s_2,...,s_m)-E(A) Gain(A)=I(s1,s2,...,sm)−E(A)
选什么样的特征作为测试特征呢?
选 G a i n ( A ) Gain(A) Gain(A)值最大的特征, G a i n ( A ) Gain(A) Gain(A)值最大即 E ( A ) E(A) E(A)>最小,也就是利用这种方法选出的测试特征对节点样本进行子集划分会使得在划分后的子集中确定任一样本类别所需的信息熵加权平均值最小;而信息熵反映的是样本的不确定程度,信息熵越大不确定程度越高,信息熵越小,不确定程度越低;也就是利用这种方法选出的测试特征会使用后续在子集中对样本类别进行判定会更简单,从而使得整个决策树更简单。
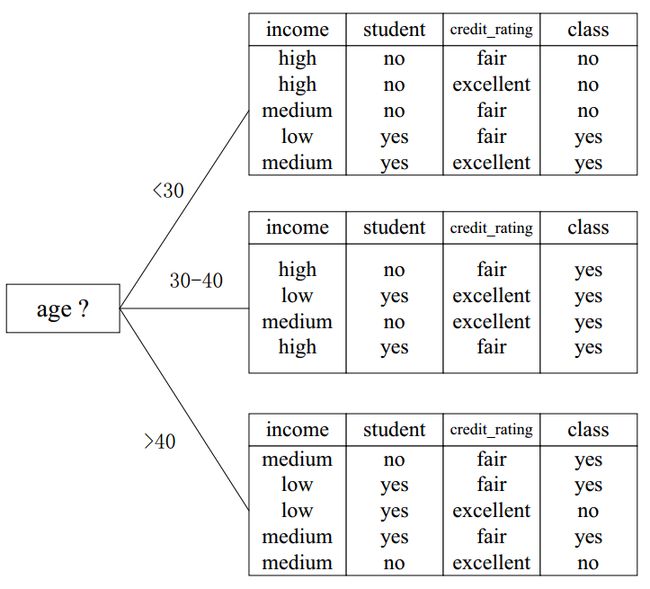
下面是《数据挖掘导论》中确定测试特征的一个例子。
样本如下:
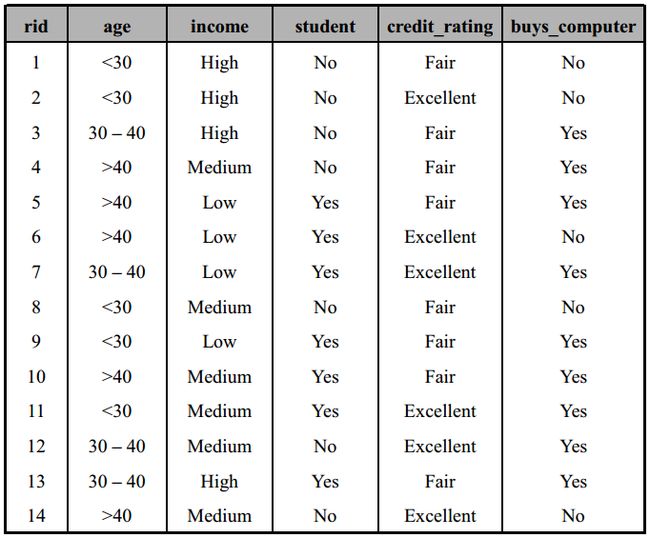
具体计算过程如下:


树枝修剪
由于噪声等因素的影响,会使得样本某些特征的取值与样本自身的类别不相匹配的情况,基于这些数据生成的决策树的某些枝叶会产生一些错误;尤其是在决策树靠近枝叶的末端,由于样本变少,这种无关因素的干扰就会突显出来;由此产生的决策树可能存在过拟合的现象。树枝修剪就是通过统计学的方法删除不可靠的分支,使得整个决策树的分类速度和分类精度得到提高。
树枝修剪包括事先修剪和事后修剪两种方法:
(1)事前修剪方法:在决策树生成分支的过程,除了要进行基础规则的判断外,还需要利用统计学的方法对即将分支的节点进行判断,比如统计 χ 2 \chi ^{2} χ2或统计信息增益,如果分支后使得子集的样本统计特性不满足规定的阈值,则停止分支;但是阈值如何选取才合理是比较困难的。
(2)事后修剪方法:在决策树充分生长后,修剪掉多余的分支。根据每个分支的分类错误率及每个分支的权重,计算该节点不修剪时预期分类错误率;对于每个非叶节点,计算该节点被修剪后的分类错误率,如果修剪后分类错误率变大,即放弃修剪;否则将该节点强制为叶节点,并标记类别。产生一系列修剪过的决策树候选之后,利用测试数据(未参与建模的数据)对各候选决策树的分类准确性进行评价,保留分类错误率最小的决策树。
除了利用分类错误率进行树枝修剪,也可以利用决策树的编码长度进行修剪。所谓最佳决策树是编码长度最短的决策树,这种修剪方法利用最短描述长度(MDL)原则来进行决策树的修剪。该方法基于的思想是:最简单的就是最好的。
CART树算法的剪枝
CART树剪枝例子
CCP剪枝法步骤(1)
生成子树序列 T 0 , T 1 , . . . , T n {T_0,T_1,...,T_n} T0,T1,...,Tn的基本思想是从 T 0 T_0 T0开始,裁剪 T i T_i Ti中关于训练数据集误差增加最小的分枝来得到 T i + 1 T_{i+1} Ti+1。实际上,当1棵树 T T T在节点 t t t处剪枝时,它的误差增加直观上认为是 R ( t ) − R ( T t ) R(t)−R(T_t) R(t)−R(Tt),其中, R ( t ) R(t) R(t)为在节点 t t t的子树被裁剪后节点 t t t的误差, R ( T t ) R(T_t) R(Tt)为在节点 t t t的子树没被裁剪时子树 T t T_t Tt的误差。然而,剪枝后,T的叶子数减少了 L ( T t ) − 1 L(T_t)−1 L(Tt)−1,因为是二叉树,其中, L ( T t ) L(T_t) L(Tt)为子树 T t T_t Tt的叶子数,也就是说,T的复杂性减少了。因此,考虑树的复杂性因素,树分枝被裁剪后误差增加率由下式决定:
α = R ( t ) − R ( T t ) L ( T t ) − 1 α=\frac{R(t)−R(T_t)}{L(T_t)−1} α=L(Tt)−1R(t)−R(Tt)
其中, R ( t ) R(t) R(t)表示节点 t t t的子树被裁剪后节点t的误差, R ( t ) = r ( t ) ∗ p ( t ) R(t)=r(t)∗p(t) R(t)=r(t)∗p(t), r ( t ) r(t) r(t)是节点 t t t的误差率, p ( t ) p(t) p(t)是节点 t t t上的样本个数与训练集中样本个数的比例。 R ( T t ) R(T_t) R(Tt)表示节点 t t t的子树没被裁剪时子树 T t T_t Tt的误差,即子树 T t T_t Tt上所有叶子节点的误差之和。
T i + 1 T_{i+1} Ti+1就是选择 T i T_i Ti中具有最小 α α α值所对应的剪枝树。
例如:图1中 t i t_i ti表示决策树中第i个节点,A、B表示训练集中的两个类别,A、B之后的数据表示落入该节点分别属于A类、B类的样本个数。
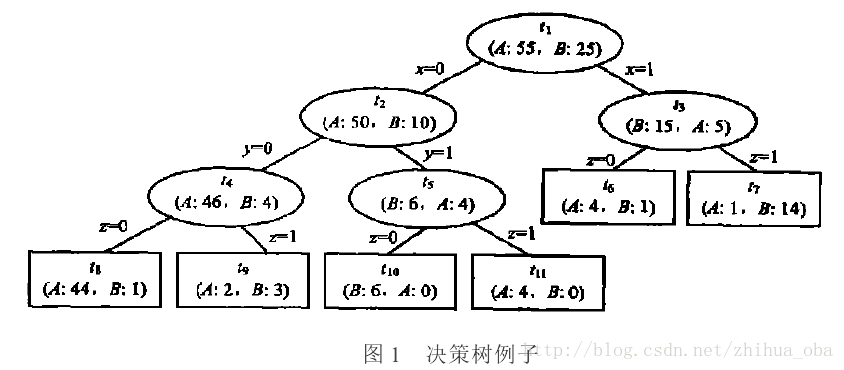
图1,决策树中训练样本总个数为80。对于节点 t 4 t_4 t4,其中,A类样本46个,B类样本4个,根据大多数原则,则节点 t 4 t_4 t4中样本为A类,故节点 t 4 t_4 t4的子树 ( t 8 、 t 9 ) (t_8、t_9) (t8、t9)被裁剪之后 t 4 t_4 t4的误差为: 4 50 ∗ 50 80 = 4 80 \frac{4}{50}∗\frac{50}{80}=\frac{4}{80} 504∗8050=804(少数服从多数,这50个都会被判定为A类,因而有4个错误)。节点 t 4 t_4 t4的子树 ( t 8 、 t 9 ) (t_8、t_9) (t8、t9)被裁剪之前 t 4 t_4 t4的误差为: 1 45 ∗ 45 80 + 2 5 ∗ 5 80 = 3 80 \frac{1}{45}∗\frac{45}{80}+\frac{2}{5}∗\frac{5}{80}=\frac{3}{80} 451∗8045+52∗805=803。故 α ( t 4 ) = 4 80 − 3 80 2 − 1 = 0.0125 α(t_4)=\frac{\frac{4}{80}−\frac{3}{80}}{2−1}=0.0125 α(t4)=2−1804−803=0.0125。类似过程,依次得到所有节点的误差增加率,如表2:

参考文献
[1] 魏红宁. 决策树剪枝方法的比较[J]. 西南交通大学学报, 2005, 40(1):44-48.
[2] 张宇. 决策树分类及剪枝算法研究[D]. 哈尔滨理工大学, 2009.
[3] Breiman L, Friedman J H, Olshen R, et al. Classification and Regression Trees[J]. Biometrics, 1984, 40(3):358.
也可以参考下面的理解
来源:
CART回归树和CART分类树的剪枝策略除了在度量损失的时候一个使用均方差,一个使用基尼系数,算法基本完全一样,这里我们一起来讲。
由于决策时算法很容易对训练集过拟合,而导致泛化能力差,为了解决这个问题,我们需要对CART树进行剪枝,即类似于线性回归的正则化,来增加决策树的泛化能力。但是,有很多的剪枝方法,我们应该这么选择呢?CART采用的办法是后剪枝法,即先生成决策树,然后产生所有可能的剪枝后的CART树,然后使用交叉验证来检验各种剪枝的效果,选择泛化能力最好的剪枝策略。
也就是说,CART树的剪枝算法可以概括为两步,第一步是从原始决策树生成各种剪枝效果的决策树,第二部是用交叉验证来检验剪枝后的预测能力,选择泛化预测能力最好的剪枝后的数作为最终的CART树。
首先我们看看剪枝的损失函数度量,在剪枝的过程中,对于任意的一刻子树T,剪枝后其损失函数为:
R α ( T t ) = R ( T t ) + α L ( T t ) R_α(T_t)=R(T_t)+αL(T_t) Rα(Tt)=R(Tt)+αL(Tt)
其中, α α α为正则化参数(树分枝被裁剪后误差增加率),这和线性回归的正则化一样。 R ( T t ) R(T_t) R(Tt)为训练数据的预测误差,分类树是用基尼系数度量,回归树是均方差度量。 L ( T t ) L(T_t) L(Tt)是子树 T T T的叶子节点的数量。
当 α = 0 α=0 α=0时,即没有正则化,原始的生成的CART树即为最优子树。当 α = ∞ α=∞ α=∞时,即正则化强度达到最大,此时由原始的生成的CART树的根节点组成的单节点树为最优子树。当然,这是两种极端情况。一般来说, α α α越大,则剪枝剪的越厉害,生成的最优子树相比原生决策树就越偏小。对于固定的 α α α,一定存在使损失函数 R α ( T ) R_α(T) Rα(T)最小的唯一子树。
看过剪枝的损失函数度量后,我们再来看看剪枝的思路,对于位于节点t的任意一颗子树 T t T_t Tt,如果没有剪枝,它的损失是
R α ( T t ) = R ( T t ) + α L ( T t ) R_α(T_t)=R(T_t)+αL(T_t) Rα(Tt)=R(Tt)+αL(Tt)
如果将其剪掉,仅仅保留根节点,则损失是
R α ( T ) = R ( T ) + α R_α(T)=R(T)+α Rα(T)=R(T)+α
当 α = 0 α=0 α=0或者 α α α很小时,$R_α(T_t)
R α ( T t ) = R α ( T ) R_α(T_t)=R_α(T) Rα(Tt)=Rα(T)
。当 α α α继续增大时不等式反向,也就是说,如果满足下式:
α = R ( T ) − R ( T t ) L ( T t ) − 1 α=\frac{R(T)−R(T_t)}{L(T_t)−1} α=L(Tt)−1R(T)−R(Tt)
T t T_t Tt和T有相同的损失函数,但是 T T T节点更少,因此可以对子树 T t T_t Tt进行剪枝,也就是将它的子节点全部剪掉,变为一个叶子节点 T T T。
最后我们看看CART树的交叉验证策略。上面我们讲到,可以计算出每个子树是否剪枝的阈值 α α α,如果我们把所有的节点是否剪枝的值 α α α都计算出来,然后分别针对不同的 α α α所对应的剪枝后的最优子树做交叉验证。这样就可以选择一个最好的 α α α,有了这个 α α α,我们就可以用对应的最优子树作为最终结果。
好了,有了上面的思路,我们现在来看看CART树的剪枝算法。
输入: CART树建立算法得到的原始决策树T。
**输出:**最优决策子树 T α T_α Tα。
算法过程如下:
- 1)初始化 α m i n = ∞ α_min=∞ αmin=∞, 最优子树集合 ω = T ω={T} ω=T。
- 2)从叶子节点开始自下而上计算各内部节点 t t t的训练误差损失函数 R α ( T t ) R_α(T_t) Rα(Tt)(回归树为均方差,分类树为基尼系数), 叶子节点数 L ( T t ) L(T_t) L(Tt),以及正则化阈值 α = m i n { R ( T ) − R ( T t ) L ( T t ) − 1 , α m i n } α=min\{\frac{R(T)−R(T_t)}{L(T_t)−1},α_{min}\} α=min{L(Tt)−1R(T)−R(Tt),αmin}, 更新 α m i n = α α_{min}=α αmin=α。
-
- 得到所有节点的 α α α值的集合M。
- 4)从M中选择最大的值 α k α_k αk,自上而下的访问子树 t t t的内部节点,如果 R ( T ) − R ( T t ) L ( T t ) − 1 ≤ α k \frac{R(T)−R(T_t)}{L(T_t)−1}≤α_k L(Tt)−1R(T)−R(Tt)≤αk时,进行剪枝。并决定叶节点 t t t的值。如果是分类树,则是概率最高的类别,如果是回归树,则是所有样本输出的均值。这样得到 α k α_k αk对应的最优子树 T k T_k Tk
- 5)最优子树集合 ω = ω ∪ T k ω=ω∪T_k ω=ω∪Tk, M = M − { α k } M=M−\{α_k\} M=M−{αk}。
-
- 如果M不为空,则回到步骤4。否则就已经得到了所有的可选最优子树集合 ω ω ω。
-
- 采用交叉验证在 ω ω ω选择最优子树 T α T_α Tα
sklearn中决策树剪枝
采用预剪枝的方式。
主要靠以下几个参数来控制
criterion='gini', 选用基尼系数作为选择特征的分裂点max_depth=None, 树的最大深度min_samples_split=2, 分裂点的样本个数min_samples_leaf =1, 叶子节点的样本个数max_leaf_nodes=None,最大的叶子节点数
Python实现决策树剪枝处理
https://blog.csdn.net/wzmsltw/article/details/51057311
决策树中分类规则的获取
决策树中的分类知识可以被抽取出来并用IF-THEN的形式加以表示,从根节点到任意一叶节点的一条路径就构成了一个分类规则。路径上的特征-值偶对就是IF-THEN中的条件部分(IF部分),叶节点的类别就是结论部分(THEN部分)。
基本决策树的改进(C4.5)
这里的改进主要是针对样本特征来作。
(1)基本决策树要求特征A取值为离散值,如果A是连续值,假如A有v个取值,则对特征A的测试可以看成是对v-1个可能条件的测试,其实可以把这个过程看成是离散化的过程,只不过这种离散的值间隙会相对小一点;当然也可以采用其他方法,比如将连续值按段进行划分,然后设置亚变量;
(2)特征A的每个取值都会产生一个分支,有的时候会导致划分出来的子集样本量过小,统计特征不充分而停止继续分支,这样在强制标记类别的时候也会带来局部的错误。针对这种情况可以采用A的一组取值作为分支条件;或者采用二元决策树,每一个分支代表一个特征取值的情况(只有是否两种取值)。
(3)某些样本在特征A上值缺失,针对这种空值的情况,可以采用很多方法,比如用其他样本中特征A出现最多的值来填补空缺,比如采用均值、中值等,甚至在某些领域的数据中可以采用样本内部的平滑来补值,当样本量很大的时候也可以丢弃这些有缺失值的样本。
(4)随着数据集的不断减小,子集的样本量会越来越小,所构造出的决策树就可能出现碎片、重复、复制等总是。这时可以利用样本的原有特征构造新的特征进行建模;
(5)信息增益法会倾向于选择取值比较多的特征(这是信息熵的定义决定了的),针对这一问题,人们提出了增益比率法(gain ratio),将每个特征取值的概率考虑在内,及gini索引法, χ 2 \chi ^{2} χ2条件统计表法和G统计法等。
补充C4.5中增益比率的计算:
G a i n R a t i o ( A ) = G a i n ( A ) S p l i t I n f o ( A ) S p l i t I n f o ( A ) = − ∑ i = 1 v s i s l o g 2 ( s s i ) GainRatio(A)=\frac{Gain(A)}{SplitInfo(A)} \\ SplitInfo(A)=-\sum_{i=1}^{v}\frac{s_i}{s}log_2(\frac{s}{s_i}) GainRatio(A)=SplitInfo(A)Gain(A)SplitInfo(A)=−i=1∑vssilog2(sis)
SplitInfo(A)反映的是按照特征A对样本进行划分的广度和均匀度。
Gini索引
CART分类树算法使用基尼系数来代替信息增益比,基尼系数代表了模型的不纯度,基尼系数越小,则不纯度越低,特征越好。这和信息增益(比)是相反的。
具体的,在分类问题中,假设有K个类别,第k个类别的概率为 p k p_k pk, 则基尼系数的表达式为:
G i n i ( p ) = ∑ k = 1 K p k ∗ ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 Gini(p)=\sum_{k=1}^{K}p_k*(1-p_k)=1-\sum_{k=1}^{K}p_k^2 Gini(p)=k=1∑Kpk∗(1−pk)=1−k=1∑Kpk2
如果是二类分类问题,计算就更加简单了,如果属于第一个样本输出的概率是p,则基尼系数的表达式为:
G i n i ( p ) = 2 p ( 1 − p ) Gini(p)=2p(1-p) Gini(p)=2p(1−p)
对于个给定的样本D,假设有K个类别, 第k个类别的数量为 c k c_k ck,则样本D的基尼系数表达式为:
G i n i ( D ) = 1 − ∑ k = 1 K ( ∣ c k ∣ ∣ d ∣ ) 2 Gini(D)=1-\sum_{k=1}^{K}(\frac{\left | c_k \right |}{\left | d \right |})^{2} Gini(D)=1−k=1∑K(∣d∣∣ck∣)2
类别分布越平均,Gini值越大,类分布越不均匀,Gini值越小。在寻找最佳的分类特征和阈值时,评判标准为:argmax(Gini-GiniLeft-GiniRight),即寻找最佳的特征f和阈值th,使得当前节点的Gini值减去左子节点的Gini和右子节点的Gini值最大。
决策树的算法实现(ID3)
本代码为machine learning in action 第三章例子
# -*- coding: utf-8 -*-
from math import log
#创建数据的函数
def createDataSet():
dataSet = [[1,1,'yes'],
[1,1, 'yes'],
[1,0,'no'],
[0,1,'no'],
[0,1,'no']]
labels = ['no surfacing','flippers']
return dataSet, labels
#计算给定数据shangnon熵的函数:
def calcShannonEnt(dataSet):
#calculate the shannon value
numEntries = len(dataSet)
labelCounts = {}
for featVec in dataSet: #create the dictionary for all of the data 获取样本中各类别数目
currentLabel = featVec[-1]
if currentLabel not in labelCounts.keys():
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1
shannonEnt = 0.0
for key in labelCounts:
prob = float(labelCounts[key])/numEntries
shannonEnt -= prob*log(prob,2) #get the log value
return shannonEnt
#划分数据集,获得特征取某一值的样本,即获得子集
def splitDataSet(dataSet, axis, value):
retDataSet = []
for featVec in dataSet:
if featVec[axis] == value: #abstract the fature
reducedFeatVec = featVec[:axis]
reducedFeatVec.extend(featVec[axis+1:])
retDataSet.append(reducedFeatVec)
return retDataSet
#选择最大信息增益的特征
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0])-1 #获取特征数目
baseEntropy = calcShannonEnt(dataSet) #在样本集合中确定任一样本类别所需的信息熵
bestInfoGain = 0.0; bestFeature = -1 #初始化最大信息增益和测试特征
for i in range(numFeatures): #逐个特征计算信息增益,并选出最大信息增益和确定测试特征
featList = [example[i] for example in dataSet] #获取所有样本的某个特征值
uniqueVals = set(featList)
newEntropy = 0.0
for value in uniqueVals: #按特征不同取值划分样本并计算加权信息熵
subDataSet = splitDataSet(dataSet, i , value) #获得特征取某一值的样本,即获得子集
prob = len(subDataSet)/float(len(dataSet)) #计算该子集在总样本中的权重
newEntropy +=prob * calcShannonEnt(subDataSet) #计算子集中确定分类所需的信息熵,并求加权平均
infoGain = baseEntropy - newEntropy #计算信息增益
if(infoGain > bestInfoGain):
bestInfoGain = infoGain #获取最大信息增益,从而获取测试特征
bestFeature = i #测试特征的索引
return bestFeature
#递归创建树用于找出出现次数最多的类别(少数服从多数)
def majorityCnt(classList):
classCount = {}
for vote in classList:
if vote not in classCount.keys(): classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0]
#创建树
def createTree(dataSet, labels):
labels=list(labels)#python中使用"="产生的新变量,虽然名称不一样,但都指向同一个内存地址,实际上两者是一样的,为了产生真正的新变量,避免后面del()函数对原变量值产生影响,这里使用变量类型转换来赋值
classList = [example[-1] for example in dataSet] #获取分类标签
# the type is the same, so stop classify
if classList.count(classList[0]) == len(classList): #所有样本类别相同,则停止分支
return classList[0]
# traversal all the features and choose the most frequent feature
if (len(dataSet[0]) == 1): #特征列表为空,强制生成叶节点,并标记类别
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) #产生测试特征
bestFeatLabel = labels[bestFeat]
myTree = {bestFeatLabel:{}} #初始化树,树通过字典存放
del(labels[bestFeat]) #逐步缩减特征规模
#get the list which attain the whole properties
featValues = [example[bestFeat] for example in dataSet]
uniqueVals = set(featValues)
for value in uniqueVals:
subLabels = labels[:]
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value), subLabels) #递归进行分支,决策树逐步生长,该决策树是存放在字典中,字典有键值对并很方便地实现层层嵌套
return myTree
#利用决策树进行样本类别预测
def classify(inputTree, featLabels, testVec): #这里只能对单个样本进行预测
for ky in inputTree.keys():
#firstStr = inputTree.keys()[0]
secondDict = inputTree[ky]
#featIndex = featLabels.index(firstStr)
featIndex = featLabels.index(ky) #ky是根节点代表的特征,featIndex是取根节点特征在特征列表的索引,方便后面对输入样本逐变量判断
for key in secondDict.keys(): #这里每一个key值对应的是根节点特征的不同取值
if testVec[featIndex] == key: #找到输入样本在决策树中的由根节点往下走的路径
if type(secondDict[key]).__name__ == 'dict': #该分支产生了一个内部节点,则在决策树中继续同样的操作查找路径
classLabel = classify(secondDict[key], featLabels, testVec)
else: classLabel = secondDict[key] #该分支产生是叶节点,直接取值就得到类别
return classLabel
#使用决策树
myDat, labels = createDataSet() #产生训练数据和特征列表
myTree = createTree(myDat,labels) #创建决策树
print(myTree)
input_type=classify(myTree,labels,[1,0])#利用决策树对输入样本类别进行预测
print(input)
这个例子是算法ID3的实现,虽然预测类别部分每次只能对单个样本进行,也没有画出决策树,但很好演示了决策树的基本思路和流程。
更完善的算法可参考sklearn库中的算法,详情可参考https://github.com/scikit-learn/scikit-learn/blob/master/sklearn/tree/tree.py
决策树之CART
https://blog.csdn.net/zhihua_oba/article/details/72230427
主要是剪枝的过程讲得很清楚
决策树模型多分类
决策树模型天然是一个多分类算法
决策树模型求解回归问题
来源:
实际生活中很多问题都是非线性的,不可能使用全局线性模型来拟合任何数据。一种可行的方法是将数据集切分成很多份易建模的数据,然后利用线性回归技术来建模。如果首次切分后仍然难以拟合线性模型就继续切分。在这种切分方式下,树结构和回归法就相当有用。
回归树与分类树的思路类似,但叶节点的数据类型不是离散型,而是连续型,对CART稍作修改就可以处理回归问题。CART算法用于回归时根据叶子是具体指还是另外的机器学习模型又可以分为回归树和模型树。但无论是回归树还是模型树,其适用场景都是:标签值是连续分布的,但又是可以划分群落的,群落之间是有比较鲜明的区别的,即每个群落内部是相似的连续分布,群落之间分布确是不同的。所以回归树和模型树既算回归,也称得上分类回归是为了处理预测值是连续分布的情景,其返回值应该是一个具体预测值。回归树的叶子是一个个具体的值,从预测值连续这个意义上严格来说,回归树不能称之为“回归算法”。因为回归树返回的是“一团”数据的均值,而不是具体的、连续的预测值(即训练数据的标签值虽然是连续的,但回归树的预测值却只能是离散的)。所以回归树其实也可以算为“分类”算法,其适用场景要具备“物以类聚”的特点,即特征值的组合会使标签属于某一个“群落”,群落之间会有相对鲜明的“鸿沟”。如人的风格是一个连续分布,但是却又能“群分”成文艺、普通和2B三个群落,利用回归树可以判断一个人是文艺还是2B,但却不能度量其有多文艺或者多2B。所以,利用回归树可以将复杂的训练数据划分成一个个相对简单的群落,群落上可以再利用别的机器学习模型再学习。
模型树的叶子是一个个机器学习模型,如线性回归模型,所以更称的上是“回归”算法。利用模型树就可以度量一个人的文艺值了。
回归树和模型树也需要剪枝,剪枝理论和分类树相同。为了获得最佳模型,树剪枝常采用预剪枝和后剪枝结合的方法进行。
那么如何利用CART构建回归树或者模型树呢?
1,回归树-利用差值选择分支特征
树回归中,为成功构建以分段常数为叶节点的树,需要度量出数据的一致性。分类决策树创建时会在给定节点时计算分类数据的混乱度。那么如何计算连续型数值的混乱度呢? 事实上, 在连续数据集上计算混乱度是非常简单的–度量按某一特征划分前后标签数据总差值,每次选取使数据总差值最小的那个特征做最佳分支特征为了对正负差值同等看待,一般使用绝对值或平方值来代替上述差值)。为什么选择计算差值呢》差值越小,相似度越高,越可能属于一个群落咯。那么如果选取方差做差值,总方差的计算方法有两种:
(1)计算数据集均值std,计算每个数据点与std的方差,然后n个点求和。
(2)计算数据集方差var,然后var_sum = var*n,n为数据集数据数目。Python Matrix中可以利用var方法求得数据集方差,因此该方法简单、方便。
与Gini Gain对离散特征和连续特征的处理方法类似,多值离散特征需要选择最优二分序列,连续特征则要找出最优分裂点。
那么,每次最佳分支特征的选取过程为:
function chooseBestSplitFeature()
(1)先令最佳方差为无限大bestVar=inf。
(2)依次计算根据某特征(FeatureCount次迭代)划分数据后的总方差currentVar(,计算方法为:划分后左右子数据集的总方差之和),如果currentVarbestVar=currentVar.
(3)返回最佳分支特征、分支特征值(离散特征则为二分序列、连续特征则为分裂点的值),左右分支子数据集。
2,采取线性回归预测偏差构建模型树
用树来对数据建模,除了把叶节点简单地设定为常数值之外,还有一种方法是把叶节点设定为分段线性函数,这里所谓的分段线性(piecewise linear)是指模型由多个线性片段组成,这就是模型树。模型树的可解释性是它优于回归树的特点之一。另外,模型树也具有更髙的预测准确度。
模型树的创建过程大体上与回归树是一样的,区别就在于递归过程中最佳分支特征选取时差值的计算。对于模型树:给定的数据集先用线性的模型来对它进行拟合,然后计算真实的目标值与模型预测值间的差值,将这些差值的平方求和就得到了所需的总差值,最后依然选取总差值最小的特征做分支特征。至于线性回归采用哪种解法,就要参看线性回归模型的求解了。
其他判断标准:
1. SSE
S S E = ∑ i ∈ S 1 ∣ y i − y ˉ 1 ∣ + ∑ i ∈ S 2 ∣ y i − y ˉ 2 ∣ SSE=∑_{i∈S_1}|y_i−\bar{y}_1|+∑_{i∈S_2}|y_i−\bar{y}2| SSE=i∈S1∑∣yi−yˉ1∣+i∈S2∑∣yi−yˉ2∣
y ˉ 1 \bar{y}_1 yˉ1, y ˉ 2 \bar{y}_2 yˉ2分别表示以当前属性作为划分选择时各自对应的集合 S 1 S_1 S1 和$ S_2$目标值的均值。可通过如下的剪枝方式提高魔性的泛化能力:
S S E c p = S S E + c p × S t SSE_{c_p}=SSE+c_p×S_t SSEcp=SSE+cp×St
S t S_t St用来定义树的规模,也即终端节点的数目。 c p c_p cp 则为可调参数,更小的 c p c_p cp将会获得更大的树,该参数可通过交叉验证的方式获得。
2. OLS regression: sum of squared error
3. quantile regression:
CART回归树建立算法
CART回归树和CART分类树的建立算法大部分是类似的,所以这里我们只讨论CART回归树和CART分类树的建立算法不同的地方。
首先,我们要明白,什么是回归树,什么是分类树。两者的区别在于样本输出,如果样本输出是离散值,那么这是一颗分类树。如果果样本输出是连续值,那么那么这是一颗回归树。
除了概念的不同,CART回归树和CART分类树的建立和预测的区别主要有下面两点:
1)连续值的处理方法不同
2)决策树建立后做预测的方式不同。
对于连续值的处理,我们知道CART分类树采用的是用基尼系数的大小来度量特征的各个划分点的优劣情况。这比较适合分类模型,但是对于回归模型,我们使用了常见的和方差的度量方式,CART回归树的度量目标是,对于任意划分特征A,对应的任意划分点s两边划分成的数据集D1和D2,求出使D1和D2各自集合的均方差最小,同时D1和D2的均方差之和最小所对应的特征和特征值划分点。表达式为:
m i n A , s [ m i n c 1 ∑ x i ∈ D 1 ( A , s ) ( y i − c 1 ) 2 + m i n c 2 ∑ x i ∈ D 2 ( A , s ) ( y i − c 2 ) 2 ] min_{A,s}\left[min_{c_1}∑_{x_i∈D_1(A,s)} (y_i−c_1)^2+min_{c_2}∑_{x_i∈D_2(A,s)}(y_i−c_2)^2\right] minA,s⎣⎡minc1xi∈D1(A,s)∑(yi−c1)2+minc2xi∈D2(A,s)∑(yi−c2)2⎦⎤
其中,c1为D1数据集的样本输出均值,c2为D2数据集的样本输出均值。
对于决策树建立后做预测的方式,上面讲到了CART分类树采用叶子节点里概率最大的类别作为当前节点的预测类别。而回归树输出不是类别,它采用的是用最终叶子的均值或者中位数来预测输出结果。
除了上面提到了以外,CART回归树和CART分类树的建立算法和预测没有什么区别。
scikit-learn中的决策树
来源:scikit-learn决策树算法类库使用小结
并行决策树
决策树模型的检验
决策树模型的评估方法
其他资料:
决策树算法原理(下)