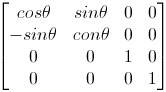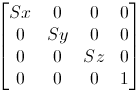Shader相关的基础数学知识整理(持续补充
Shader相关的基础数学知识整理(持续补充)
向量：
即unity3d中的Vector，向量可以形象化地表示为带箭头的线段。箭头所指：代表向量的方向；线段长度：代表向量的大小。
Unity3d 中Vector2, Vector3, Vector4分别代表二维，三维，四维向量。
单位向量：
如果x²+y²+z²=1，即向量的模为1，则向量{x,y,z}称为单位向量。Shader内置的normalize方法即是对向量进行标准化的
向量的点乘：
向量a·向量b=|a||b|cos ，结果是一个数量（没有方向）。
向量的数量积的运算律
a·b=b·a（交换律）
(λa)·b=λ(a·b)(关于数乘法的结合律)
（a+b)·c=a·c+b·c（分配律）
两个单位向量的点乘结果是向量夹角的cos值。shader最常见的用法是计算光照的强度，如：saturate(dot(s.Normal,lightDir));
这句代码用法线用入射光的的单位向量点乘法光线的夹角cos值（法线跟入射角都已经是单位向量了） 夹角越小，值越大，散射越强 颜色越亮，saturate方法等价于max(0, dot(s.Normal, lightDir));
向量的叉乘：
|向量c|=|向量a×向量b|=|a||b|sin ，结果是一个向量，方向与所在的平面垂直,且方向要用“右手法则”判断（用右手的四指先表示向量a的方向,然后手指朝着手心的方向摆动到向量b的方向,大拇指所指的方向就是向量c的方向）。顶点的Tangent Space就是用向量的叉乘计算得到的。
unity3d 内置的TANGENT_SPACE_ROTATION计算模型空间到切空间转換矩阵rotation的计算代码:
float3 binormal = cross( v.normal, v.tangent.xyz ) * v.tangent.w;// 副切线向量o.binormal通过乘以v.tangent.w计算它的长度
float3x3 rotation = float3x3( v.tangent.xyz, binormal, v.normal ) //模型到切空间转换矩阵
齐次坐标:
所谓齐次坐标就是将一个原本是n维的向量用一个n+1维向量来表示。例如，二维点(x,y)的齐次坐标表示为(hx,hy,h)。主要作用是把平移的加操作转换成了矩阵相乘操作跟旋转跟缩放矩阵统一了起来。二是可以区别点跟向量,
如果(x,y,z)是个点，则变为(x,y,z,1);
如果(x,y,z)是个向量，则变为(x,y,z,0),即最后如果是1则是点，0则是向量
这个可以用来区别点光源跟平行光源
矩阵：
在三维空间中，一般使用4x4的四维矩阵（原因看齐次坐标）。最经常的用法就是把点从一个坐标系通过跟矩阵相乘转換到另一个坐标系。
这里需要注意一点。
两个矩阵Aij和Bxy若能相乘，则必须满足j=x才行，
在directX 中，使用的是行向量，表示为[x,y,z,w].
则需左乘转换矩阵。
在opengl中，使用的是列向量，
则必需右乘转换矩阵
转置矩阵
把矩阵A的行和列互相交换所产生的矩阵称为A的转置矩阵，这一过程称为矩阵的转置
矩阵的转置满足以下运算律：
这里额外说一点。
(A×B)'= B'×A'
由这个公式我们可以知道，Opengl 中的向量跟directX中的向量互为转置向量。所以opengl中向量右乘转換矩阵：(A×B)计算出来的值需要在directx中转即，(A×B)',所以在directx中是B'×A'。即opengl中的向量跟旋转矩阵都需要转置后然后向量左乘转换矩阵，即在directx中的转换矩阵跟opengl中的转换距阵也是转置的。
转換矩阵相关：
平移变换
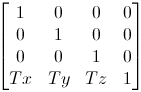
绕X轴旋转
绕Y轴旋转
绕Z轴旋转
缩放变换
统一缩放矩阵：
沿每个坐标轴同时进行缩放时（我们称为统一缩放uniformscaling），即Sx,Sy,Sz是一样的。
MVP矩阵的生成：
因为矩阵相乘满足结合律，不满足交換律
即 (M*V)*P= M*(V*P)
在DirectX中，矩阵乘法的顺序是从左到右，变换生效的先后顺序也是从左到右
Vector*trans*rotation*scale
而在OpenGL中，矩阵连乘的顺序是从右到左
scale*rotation*trans*vector